裘布依公式是在许多假定条件下推导出来的，自然界的情况通常不能完全满足这些条件，这就使公式的运用受到限制。为了正确地应用裘布依公式，必须就一些问题给予讨论。

1.关于流量与水位降深的关系

在裘布依公式中若为承压水层时二者为线性关系，而潜水层时为抛物线关系。大量的抽水实践表明，裘布依公式所反映的上述关系仅适用于小降深抽水的情况。降深较大时，水流的流态发生变化，裘布依公式计算结果偏大。

2.关于流量和井半径的关系

在裘布依公式中流量和井半径为对数关系，也就是说随着井径的增大，流量增加很少。按公式计算，井径增大一倍，流量只增加10%左右；井径增大10倍，流量只增加40%左右。但实践表明井径对流量的影响要比裘布依公式所表示的大得多。大量的事实说明：在同一含水层中，从小井径增大到中等井径时，流量增加很快，井径继续增大，则流量的增加逐渐减小。这是因为一口井的流量受两方面因素的控制：其一为含水层的出水能力；另一为井管的过水能力。而裘布依公式只考虑了含水层的出水能力。当含水层的渗透性较好，水位降深较大时，含水层能提供较大的流量。若采用了较小口径的井管，井管的过水能力有限，流量并不大，若增大井管的口径，流量就有明显的增加，但井径增加到足够大时，使井管的过水能力近于含水层的出水能力，则井径和流量的关系便与裘布依公式较为符合了。

3.关于井损

生产实践表明，抽水时井中的水位与外井壁处水位不一致，前者低于后者。这种内、外井壁处水位不一致的现象称为井损，其水位的差值称为井损值，用Δh表示（图4-16）。井中的水位降深可写成：

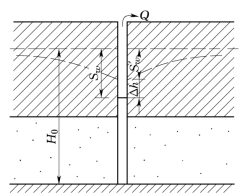
图4-16　井损及井损值Δh

式中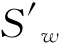为外井壁处的水位降深，它代表把流量为Q的地下水输送到外井壁处而引起的水头损失。Δh为井损值，代表把流量为Q的水输送到井中以后所引起的水头损失。通常这一部分水头损失包括以下三部分：①水流通过滤水管时，由于滤水管的摩阻引起的水头损失；②水流进入滤水管后，水流方向偏转（由水平方向为主转为垂向）引起的水头损失；③水流进入吸水设备被抽到井口引起的水头损失。

裘布依公式中没有考虑水位差的存在，所以在运用公式时：

（1）计算流量时，用井内水位hw，结果是正确的。曾有学者作过严格的数学证明。(www.daowen.com)

（2）计算浸润曲线时，当R≤H0时，计算的浸润曲线比实测曲线低，在井附近的计算曲线与实测曲线相差更大。为了得到准确的浸润曲线位置，常在井的附近打观测孔，用观测孔中的水位代入公式中去计算。如果利用抽水井水位资料进行计算时，应该对水位值进行校正。井损值可在抽水试验现场利用观测井直接测定，亦可用有关的经验公式计算，潜水井在抽水降深较大时，亦存在井内外水位不一致的现象，通常称“水跃”。关于计算水跃的方法也可查阅水文地质手册，这里不作详述。

4.关于影响半径

在推导完整井的裘布依公式时，曾假定井是位于一个以井轴为中心，以影响半径为半径的圆柱形含水层的中心，圆柱形含水层的边界上保持水位不变，即r=R处，H=H0或S=0，没有水位下降。而自然界中，这样的含水层可以说是没有的。

最先将裘布依模型应用到实践中去时，德国的齐姆提出影响半径是从抽水井起至实际上已观察不到水位降深的总的水平距离。按此概念，影响半径实际上是可以观测到的降落漏斗的半径。前面曾提到，降落漏斗是轴对称的，这种情况必须是在无限延伸的水平含水层中，初始水头线是水平的时候产生，这种条件也是不多的。自然条件下，有的潜水面或承压水头面并不水平，含水层的渗透性也不均一等等，因此，降落漏斗不是对称的，其边界也不是圆的。为简化起见，平时所说的影响半径实际上是“引用影响半径”的概念，即用一等效的圆形降落漏斗代替实际的降落漏斗，此假想的等效圆形漏斗的半径便是引用影响半径，实际上并不存在。

计算影响半径的经验公式有很多，常用的有如下两种：对于潜水井，常用库萨金公式：

对于承压水井，常用吉哈尔特公式：

尚有其他经验公式请参阅有关手册。

不同的岩土，影响半径值不同，常用的影响半径经验数据如表4-2所示。

表4-2　不同岩性影响半径经验数据值表　单位：m