研究地下水向承压水完整井运动时所作的假设，与水流向潜水完整井的假设相同，差别在于，抽水时产生的降落漏斗不在含水层中，而是在隔水顶板内形成发展。此时向井汇集的水流为稳定流。同时是一个平面径向流，地下水流向井的流线是相互平行的，且平行含水层的隔水顶底板，等水头线为一系列的与流线垂直的直线，因此，渗流断面是圆柱体侧面（图4-15）。

取柱坐标系统，以井轴与隔水底板的交点为坐标原点，井轴线为H轴，向上为正，沿隔水底板为r轴，

由井轴向外为正。当水流呈层流流态时，据达西定律

将上式分离变量并积分（取r∶rw→R，H∶H→H0），则得

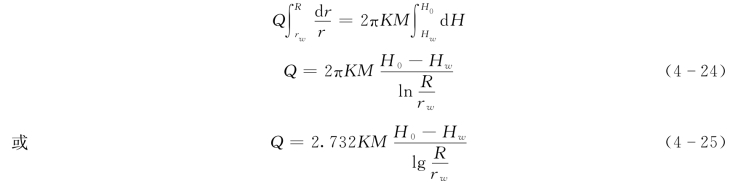
式中　M——承压含水层厚度，m；

　　　H0、Hw——分别为承压水的原始水位值及抽水井中的水位值（以隔水底板为基准面），m。

式（4-25）中如引进抽水井的水位降深值Sw，由于Sw=H0-Hw，则式（4-25）可写成

式（4-24）～式（4-26）即为地下水向承压完整井运动方程，又称裘布依公式。利用上述公式，给定抽水井的水位降深，就可以确定井的涌水量，若给定井的涌水量，也可确定抽水井中的水位降深值。此外，利用上述公式可计算含水层的渗透系数：(www.daowen.com)

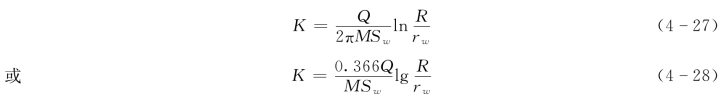
当抽水井附近有一个或两个观测井的水位资料时，同样可改变积分界限而取得K值的计算式。

有一个观测孔时

有两个观测孔时

式中　r1、r2——抽水井至观测孔1、2的距离；

　　　S1、S2——1、2号观测孔中的水位降深值。

如将式（4-29）中的r1和Sw、S1改写成距抽水井任意距离r及其相应的水头值Hw、H，可获得承压完整井抽水时的水头线方程式