为了便于分析研究，对渗流可从不同的角度进行分类。

1.稳定流与非稳定流

稳定流与非稳定流是根据渗流的运动要素是否随时间变化来划分的。如果在渗流场中任一点处，渗流的运动要素不随时间改变，这种渗流是稳定流（其运动称为稳定运动）。稳定流的运动要素与时间无关，它们是空间坐标的函数。以水头及渗流速度为例，可以表示为

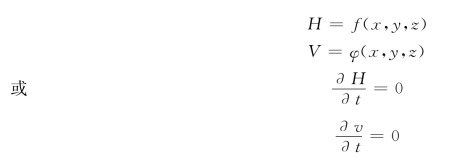
如果在渗流场中任一点处，渗流的运动要素中只要有一个是随时间变化的，则此渗流为非稳定流（其运动称为非稳定运动）。非稳定流的运动要素是时间和空间坐标的函数，以水头及渗流速度为例，可表示为

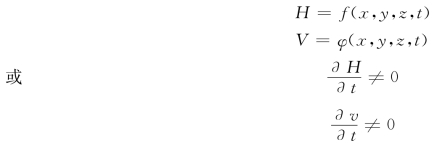
严格地说，天然条件下地下水运动都属于非稳定流。但当地下水的运动要素在某一时段内变化不大，或地下水的补给、排泄条件随时间变化不大时，为便于计算，可以近似地视为稳定流。

2.有压流与无压流

有压流与无压流是根据渗流是否具有自由表面，即自由表面上的压强是否为大气压强来划分的。如果渗流不具有自由表面，即渗流场中任一点处的压强都不为大气压（一般大于大气压强）时，这种渗流称为有压流（承压水）。如果渗流具有自由表面，自由表面上的压强为大气压强时，这种渗流则是无压流（潜水）。若两隔水层间地下水没有充满整个透水岩层时，渗流亦为无压流。

3.层流与紊流

地下水在运动时，根据水的质点是否呈有秩序地运动分为层流与紊流。水质点有秩序地呈相互平行而互不干扰的运动，称为层流运动；水质点相互干扰而无秩序的运动，称为紊流运动。天然条件下地下水在岩层空隙中的运动速度一般很小，多为层流运动，只有在空间较大的裂隙或溶穴中运动时，地下水流速大时，才可能出现紊流。

4.均匀流与非均匀流

渗流速度沿流程不变的渗流称为均匀流。均匀流沿流程渗流断面的大小、形状不变，流线呈直线相互平行[图4-2（a）]。渗流速度沿流程发生变化的渗流称为非均匀流。非均匀流的渗流断面沿流程发生变化，流线彼此不平行，且不为直线[图4-2（b）]。

在非均匀流中，根据运动要素改变程度又可分为缓变流与急变流。相邻流线之间的夹角很小，近似于平行直线的渗流，称为缓变流，反之，则为急变流。在天然条件下，地下水的运动大多为缓变流。为研究方便，在缓变流运动中，通常假定渗流过水断面为平面，且在同一断面上各点的水头值相等。

5.一维流、二维流和三维流(www.daowen.com)

根据渗流速度向量V与所选坐标系{O-XYZ}的关系，可将渗流分为一维流、二维流和三维流。

在流线相互平行的渗流场中，可选择坐标系中任一坐标轴（如OX轴）与渗流速度向量相一致，此种情形下的渗流就称为一维流（又称单向流）。图4-8所表示的隔水顶、底板呈直线平行埋藏的等厚、等宽、均质承压含水层中的渗流就属一维流。

二维流各点的速度向量均与某一平面平行（因而又有平面流之称）。因此，可选择坐标系中任一坐标面与此平面相平行（或重合），在此坐标面上可将渗流速度向量分解成两个速度分量。例如，对于两平行河流的河间地块中的潜水流（图4-9）来说，任一点处渗流速度V的方向均与XOZ平面平行，于是可沿X、Z两坐标方向将V分解成Vx及Vz两个分量。

根据二维流的特点，可以采用多个等间距分布的、且与XOZ（或XOY）平面平行的平面，把含水层分成多个运动特征完全相同的部分。于是，取一个单位宽度（或厚度）的渗流进行研究就可掌握整体渗流的运动特征。

通过单位渗流宽度的流量称为单宽流量，用q表示。通过渗流宽度为B的流量Q应为

三维流又称空间流。三维流各点的速度向量相互之间不平行。例如，在潜水含水层中抽水时，虽然各点处的渗流均沿径向向井中运动，然而渗流速度向量并不与某一平面或某一方向平行。在图4-10中的点A处，渗流速度V在三个坐标方向上的分量分别为Vx，Vy及Vz。

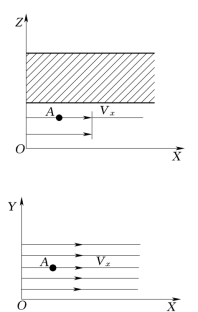
图4-8　一维流

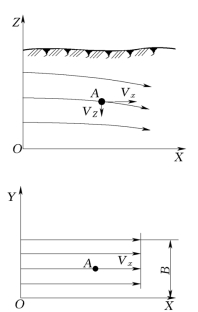
图4-9　二维流

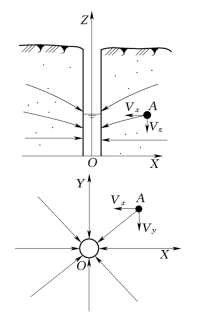
图4-10　三维流

严格地讲，自然界中的地下水流均为三维流，需要考虑运动要素在空间三个坐标方向上的变化，条件较为复杂，求解往往极为困难。通常，渗流在水平方向上的速度分量远大于垂直方向上的速度分量，因此有可能忽略后者，把三维流近似作为二维流（在某些条件下甚至可以近似作为一维流）进行研究，便于求解。