隐马尔可夫模型（hidden Markov model，HMM）是用来描述一个含有隐性未知参数，即状态的马尔可夫过程。其难点是从已观察的数据中确定该过程的隐含参数，然后利用这些参数来做进一步的分析与挖掘。对于任意一张人脸图像而言，其像素值处于可观测状态，而其隐含状态不能根据像素值观察而得到，因此需要一个随机过程去描述隐含的状态，即隐马尔可夫模型［57］。

近年来，基于隐马尔可夫模型的方法成为人脸识别领域较为主要的研究内容。基于隐马尔可夫模型的人脸识别方法可在一定程度上提升人脸识别准确率。

1.隐马尔可夫模型

隐马尔可夫模型是由两个相互关联的随机过程构成。其中一个是由内在的有限个状态的马尔可夫链来描述状态可能的变化，另一个随机过程描述观察值和所对应的状态之间的统计学关系。因为在状态转移过程中，观察者看到的只是与每一状态相关联的随机函数的输出值，观察不到具体的马尔可夫链的状态，故称之为隐马尔可夫模型。

1）隐马尔可夫模型的基本参数

隐马尔可夫模型的本质是一种用参数表示、用于描述随机过程统计特性的概率模型。隐马尔可夫过程由可观测的观察序列和不可观测的状态过程构成。隐马尔可夫模型可以表示为

其中，N为状态集合S=｛S1，S2，…，SN｝中的隐马尔可夫模型的状态数，假定t时刻的状态为qt，qt∈S，1＜t＜T，T为观察序列的长度；M为观察集合V=｛V1，V2，…，VN｝中状态所对应的观察数目；A为状态转移概率分布或转移矩阵，A=｛aij｝，aij=p（qt=Sj|qt-1=Si），1＜i＜N，1＜j＜N；B为观察概率矩阵或称之为发射矩阵，B=｛bij｝，bij=p（Ot=Vk|St=qj）；Π为初始状态概率分布矢量，Π=｛πi｝，πi=p（qi=Si），1＜i＜N。

2）参数计算和模型的建立

HMM模型建立之后，有三个基本的问题需要解决，即①给定观察序列O=o1，o2，…，or，以及模型参数λ=（N，M，A，B，Π），评估给定模型产生观察序列的概率p（O|λ）的问题；②给定观察序列O=o1，o2，…，or，以及模型参数λ=（N，M，A，B，Π），为了更好地解释观察序列O=o1，o2，…，or，如何选择一个最佳序列Q=q1，q2，…，qT的问题；③如何调整模型参数λ=（N，M，A，B，Π），使得p（O|λ）达到最大的问题。

在以上三个问题解决以后，就可以得到参数最优的模型，用于实际人脸识别。其中，第一个问题是对给定模型产生观察序列的概率进行估计，即评价模型与观察序列的匹配程度，给定一个未知人脸，计算哪个人脸模型经过状态转移生成该人脸模型的概率最大，将该未知人脸分到哪一类人脸当中。第二个是计算给定模型参数和观察序列后，生成哪种状态转移序列的可能性最大，通常需要制订一个优化准则，当满足优化准则条件后就可以认定该状态转移序列的可能性最大。第三个是对模型参数的优化问题，给定一组观察值序列后，需要不断调整优化参数λ，使得观察值出现的概率最大。

基于HMM的人脸识别就是要根据一组相同人的不同人脸图像，通过学习，给每一个人脸建立一个与之相对应的模型，这实际上是一个参数估计问题。

问题①的评估问题，采用前向后向算法来解决。

定义前向变量αt（i）为

定义后向变量βt（i）为

前向算法步骤：

a.初始化αt（i）

b.递推

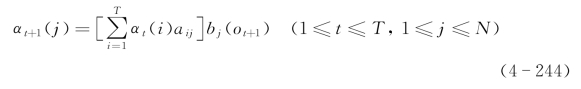
c.结束

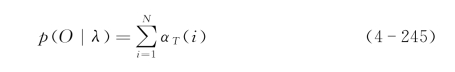
后向算法步骤：

a.初始化βt（i）

b.递推

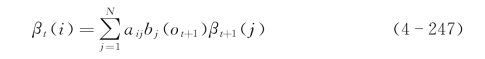
定义

表示沿着一条单路径计算前i个观察值在时刻t结束于Si状态时的最高值。那么可以推出关系式：

再用一个二维阵列｛ψt（j），t=1，2，…，T，j=1，2，…，N｝来跟踪记载δt（j）在推导过程中的最佳路径。

解决问题②的算法步骤：

a.初始化

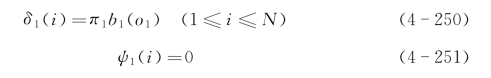
b.递推

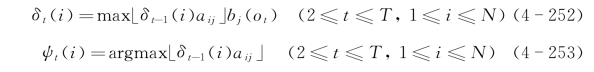
c.结束

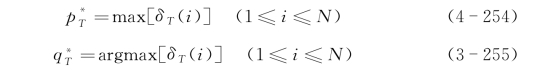
d.路径回溯（最佳状态链的确定）

算法的结果不仅给观察序列O确定了一个最佳状态链，而且可以同时求出模型λ产生观察序列O的概率p（O|λ）。由此得到的最佳状态链也确定了观察序列和各个状态之间最可能的对应关系，这种对应关系也称为对观察序列进行了分割。

如何调整模型参数λ=（N，M，A，B，Π），使p（O|λ）最大，这就是对模型参数的优化问题。受模型的训练样本个数和训练次数的限制，观察序列的长度往往也受到限制，因此不可能得到最优的参数估计值，而只能用一种估计最大化的算法来获得局部最优解。

定义1：γt（i）为给定HMM模型和观察序列在t时刻处于状态Si的概率，则

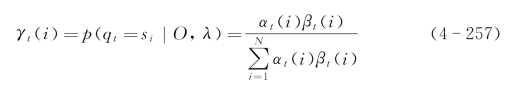
且满足条件

定义2：在t+1时刻处于状态Sj的概率为

用前后向概率表示，则有

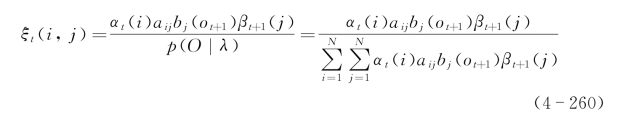
显然，γt（i）和ξt（i，j）满足

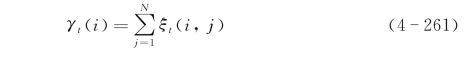
如果将γt（i）对某个时间段t求和，可以得到在时间段t内访问状态Si的次数，或者从状态Si转出的期望次数；与此相类似，将ξt（i，j）对某个时间段t求和，可以得到从状态Si转移到状态Sj的期望次数，即

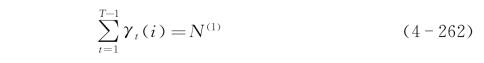
式中，N（1）为从状态Si转出的期望次数。

式中，N（2）为从状态Si转移到Sj的期望次数。

根据以上公式，可以得到对HMM模型参数的一组估计公式：

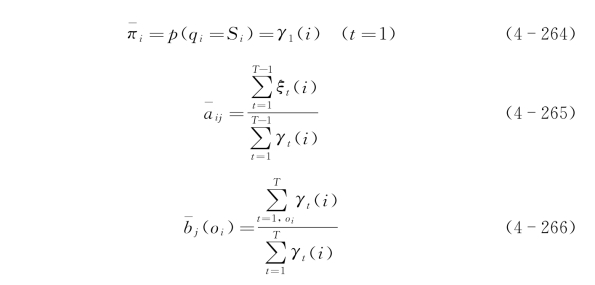
此处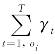，（i）表示处于状态Sj和出现观察oi的平均次数；（i）表示处于状态Sj的平均次数。

定义当前模型λ=（N，M，A，B，Π）的重估公式为=（N，M，），如果当前模型的初始参数就是一个极值点，那么在p（O|）＞p（O|λ）意义上，模型比模型λ更优。也就是说，如果能找到一个新的模型，则新的模型产生观察序列O的概率更大。(www.daowen.com)

通过理论分析可知，如果反复重复上述步骤，不断更新优化模型参数，就能够提高模型产生观察序列的概率，相当于模型利用训练样本不断学习和升级。当满足了某个限制条件的时候，重估过程就会停止，模型的学习和升级也就告一段落，此时得到的模型参数称为对的最大似然估计。

定义了一个辅助函数

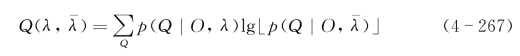
重估公式可以由上式通过对求极大值得到，并可以证明最大化Q（λ，）会导致似然概率的增大，即

最后，似然函数将会收敛到一个模型函数的极值点。

3）HMM模型的训练

实际上，隐马尔可夫模型是一个包含五个状态的左右型人脸模型。该模型将正面人脸图像分为头发、额头、眼睛、鼻子和嘴巴五个显著的特征区域。无论何种人脸，受到何种干扰，这五个区域保持从上到下的次序是不变的，可以认为每个显著的特征区域中都隐含着一个人脸的状态。因此可以说，这五个隐藏的状态可以产生一个观察序列，通过观察序列就可以估计这五个状态。

隐马尔可夫模型训练的目的就是要为每一个人建立一个与之相对应的模型，并且模型通过不断训练和学习，最终得到最优的模型参数，使得模型可以准确表示对应人脸相比于其他人脸显著的特征。HMM模型训练的流程如图4-40所示。

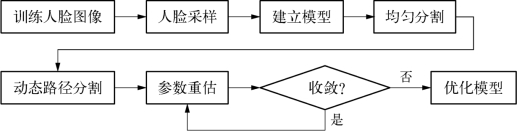
图4-40　HMM模型训练流程图

计算步骤：①用采样窗对人脸图像进行采样，并对每一个采样窗矩阵做奇异值分解，将其奇异值向量作为观察序列；②建立一个通用的HMM模型λ=（N，M，A，B，Π），确定模型的状态数、允许的状态转移和观测序列向量的大小；③将用于训练的人脸图像均匀分割成N个特征区域，分别与模型的N个状态对应，计算模型的初始参数；④用动态路径分割来重新估计模型参数的初始值；⑤参数重估并反复迭代，直至得到最优的模型参数。

在实验中，通常同时采用迭代次数和迭代误差两个量来控制收敛速度，也就是当迭代次数大于15次或前后两次的迭代误差小于e-4时，就认为已经达到了收敛。一旦获得最大化的观察概率后，训练过程立即结束。此时的模型参数为最优的模型参数，存入数据库中作为这一类人脸的标准模型。

2.隐马尔可夫模型的人脸识别过程

人脸识别过程与模型训练的步骤相同。将每个采样窗内的图像矩阵进行奇异值分解，得到观察序列。基于隐马尔可夫模型的人脸识别实际上就是通过人脸图像的像素值（观察值）来估计其隐含状态的参数——基于隐马尔可夫的人脸模型。通过观察值估算其隐含参数的过程就是建立人脸模型的过程。分别计算每个观察模型生成该序列的最大似然概率，概率最大的模型就是待识别的人脸所属的类。表达式为

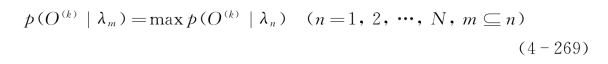
如果第m个模型λm产生序列O（k）的最大似然概率为所有概率中的最大值，说明图像k属于第m类模型。具体的识别流程如图4-41所示。

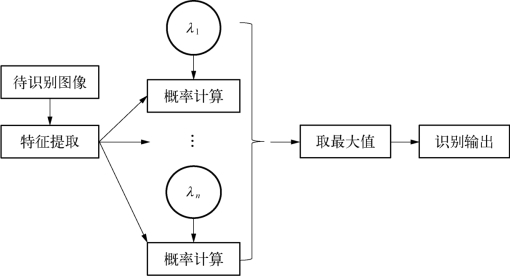
图4-41　HMM模型人脸识别流程

1）人脸采集与处理

用采样窗对被识别图像进行采样，待采样的图像如图4-42所示。

图4-42　正面人脸图像

2）奇异值向量分解

在模式识别中，特征抽取是一项至关重要的技术。特征抽取的目的是为了得到特征数量较少或特征维数较低而分类错误概率较小的特征向量。由于在实际问题中最重要的特征往往不容易找到，或是无法测量，因此如何提取简单而有效的特征成为模式识别系统一个十分重要的问题。

用于图像识别的特征可以分为直观性特征、灰度统计特征、变换系数特征以及代数特征。

（1）直观性特征。直观性特征的物理意义明确，如图像的边沿、轮廓、纹理、区域等，可以针对具体的问题设计相应的提取算法。

（2）灰度统计特征。灰度统计特征将图像看作二维随机过程，用统计意义上的各阶矩来描述图像特征，如7个矩不变量等。

（3）变换系数特征。变换系数特征对图像进行各种数学变换，用变换得到的系数来表示图像的特征，如傅里叶变换、哈夫变换、哈达玛变换等。

（4）代数特征。代数特征反映了图像的内在属性，并且具有不变性，将图像作为矩阵看待，可以进行各种矩阵分解或代数变换，如变换和主分量分析等。

目前较为常用的特征提取方法主要是代数特征提取，因为代数特征反映了图像各像素之间的统计规律。将灰度图像看作由各像素点上的灰度值构成的矩阵，可以对其进行各种矩阵分解或代数变换。

由于矩阵的特征向量反映了矩阵的代数属性，并且具有稳定性和不变性，因此可以作为表征图像的一种特征引入识别系统进行识别。

对矩阵进行奇异值分解是一种有效的代数特征提取方法。这种方法的优点在于，奇异值具有良好的稳定性，算法比较稳定和简单，奇异值具有代数和几何上的不变性，对光照、表情、姿态的变化具有一定的鲁棒性，因此在图像识别领域中应用广泛。奇异值分解在信号处理和模式识别领域中是一种求解最小二乘问题的有效工具。

任何一个实对称方阵都可经正交变换转化为对角阵，若一幅图像用实矩阵表示，则可用奇异值分解，将其转化为

其中，U、V是两个单位正交矩阵，Σ为对角阵

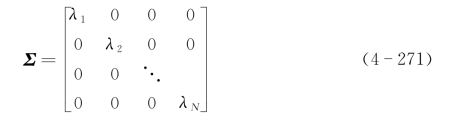
如果A只有k个非零奇异值，那么

其中，ui、vi分别是U和V的各个列元素。

取Sn×1=［λ1λ2…λN0 0 0］T为矩阵A的奇异值向量。由奇异值分解的定义可知，对任意一个实矩阵A，它的奇异值分解是唯一的。λ按序排列成λ时，图像A经过奇异值分解所得到的特征向量也应该是唯一的。因此，奇异值向量就可以作为表征灰度值矩阵的数值特征。奇异值向量具有稳定性、转置不变性、位移不变性、旋转不变性、镜像变换不变性、奇异值向量与对应图像亮度成比例变化等特性。

3）特征提取

在人脸识别特征提取过程中，最常用的是五个状态的左右型隐马尔可夫人脸模型。该模型将正面人脸图像分为头发、额头、眼睛、鼻子和嘴巴五个显著的特征区域，无论何种人脸，受到何种干扰，这五个区域均保持从上到下的次序是不变的，可以认为每个显著的特征区域中都隐含着一个人脸的状态。因此可以说，这五个隐藏的状态可以产生一个观察序列，通过该观察序列就可以估计到这五个状态，其状态结构如图4-43所示。

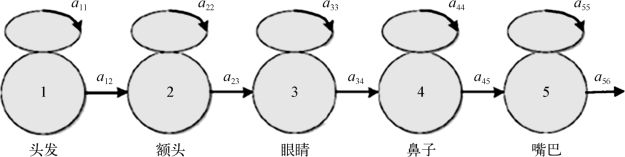
图4-43　五个状态的左右型HMM模型

图4-43中，a11、a12为转移矩阵A=｛aij｝中头发的状态转移概率分布值，即头发可观测值矩阵元素和不可观测状态概率分布值元素；a22、a23为转移矩阵A=｛aij｝中额头的状态转移概率分布值；a33、a34为转移矩阵A=｛aij｝中眼睛的状态转移概率分布值；a44、a45为转移矩阵A=｛aij｝中鼻子的状态转移概率分布值；a55、a56为转移矩A=｛aij｝中嘴巴的状态转移概率分布值。

设人脸图像尺寸为M×H，采样窗的尺寸为M×L，对图像进行从上到下的采样，两个相邻的采样窗之间重叠的部分高度为P，则采样数为

在实际中，参数L和P的取值在很大程度上影响识别率。一般情况下，P越大，采样数越多，观察序列也就更长，模型的训练次数也就越多，参数更加准确，识别率也就越高。在P足够大的情况下（P≤L-1），L对于系统识别率的影响就基本可以忽略不计了。

由于奇异值向量的稳定性及转置不变性等特性，相对于直接采用灰度值或二维离散余弦变换系数，奇异值向量作为观察向量可以得到更高的识别率。因为人脸识别中的一个难点问题是，同一个人的不同照片往往是有些差别的，光照强度、角度甚至面部表情变化都可能引起识别率的剧烈变化。灰度值作为观察向量的缺点在于，灰度值不代表稳健的图像特征，对噪声、光照、旋转十分敏感，另外大尺寸的观察向量也会增加计算的复杂度，增加系统训练和反应的时间。

4）匹配结果

图4-44所示为同一个人在不同角度下拍摄的人脸图像。为了降低由于拍摄条件变化导致的隐马尔可夫模型参数变化，也为了消除人脸隐状态（即五官）内部像素的像素值突变造成的状态转移参数变化，在建立人脸图像的隐马尔可夫模型之前，可以引入人脸图像预处理操作。即利用中值滤波器对人脸图像进行预处理之后，将预处理结果作为观察值估算隐马尔可夫模型参数。

经过中值滤波器后的人脸隐状态内部图像的像素值会趋于一致，同时人脸角度变化在人脸图像中所造成的阴影和五官变形也在一定程度被均值滤波器抵消了。因此，在隐马尔可夫模型建立之前，对人脸图像的均值滤波处理能够提升人脸模型的精度。

在人脸图像预处理后，还需要获取人脸图像的观察值序列，才能够实现隐马尔可夫模型参数的估算。为了能够在降低观察值序列维数的同时获取更高的识别精度，可以采取奇异值分解的方法获取观察值序列。比如，使用宽度为W像素，高度为L像素的滑动窗自上而下遍历整个人脸图像，相邻两个滑动窗之间重叠高度为P像素，如图4-45所示。

图4-44　不同视角下的人脸图像

图4-45　滑动窗示意图

对每个滑动窗区域的图像进行奇异值分解，分解后得到多个矩阵作为该滑动窗区域图像的观察值，所有滑动窗经过的图像部分的观察值为组成该幅人脸图像的观察值蓄序列。

上述计算过程完成后即可建立人脸隐马尔可夫模型，即通过数据库中的人脸图像获取该人脸的隐马尔可夫模型参数。

人脸隐马尔可夫模型的识别过程为计算其属于每个人脸隐马尔可夫模型的概率，概率最大的隐马尔可夫模型为识别结果。具体过程如下：①对滤波后图像进行滑动窗分割，并计算每个窗口的观察值；②用获取的观察值计算与每一个隐马尔可夫模型的匹配程度；③选取概率最大的隐马尔可夫模型作为识别结果。

如图4-46所示为同一个人在不同角度且在不同时段所拍摄的人脸图像，采用HMM模型识别取得准确的识别样本。

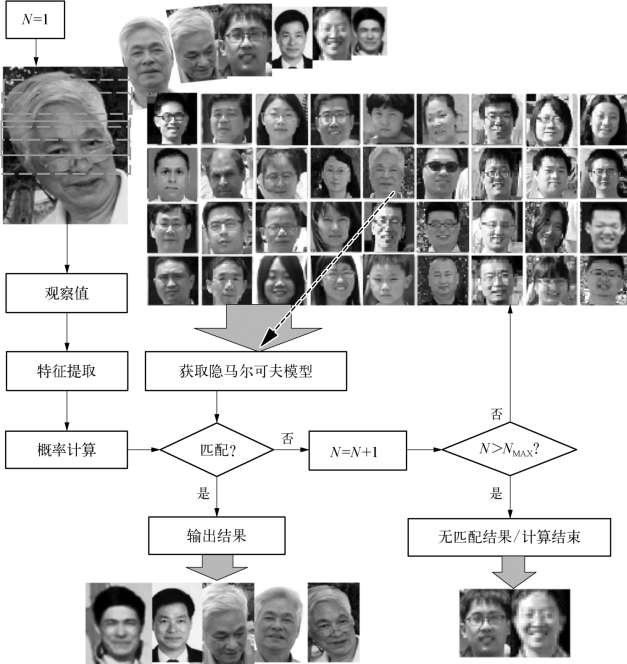
图4-46　基于隐马尔可夫模型的识别示意图