支持向量机（SVM）以统计学习理论为坚实基础，由于其优越性，自提出来后受到了各个领域的关注和研究。目前针对SVM的研究主要集中在本身性质的理论研究、大型问题的有效算法以及应用领域的推广等。其中，应用研究方面已经取得了大量的研究成果，除了上述“二分类支持向量机”运用于列车动力系统及其传动装置状态识别之外，还将“多分类支持向量机”应用于人脸检测和识别、网络入侵检测、手写体文字识别等技术领域［24］。在人脸识别应用中，首先利用主成分分析（PCA）减少直方图的维数，再使用支持向量机进行分类，因而能够提高识别速率。该识别系统的基本流程如图4-37所示。

图4-37　SVM人脸识别流程图

1.多分类支持向量机

非线性支持向量机通过建立非线性变换将样本从所在输入空间映射到一个特征空间，使得原有超曲面模型对应于特征空间的超平面模型，实现在高维特征空间中样本的线性可分。其拓扑结构如图4-38所示。

给定训练集

其中，xl∈Rn，yl∈Y=｛1，2，…，M｝，i=1，2，…，l。据此寻找空间Rn上的一个决策函数f（x）：Rn→Y，用以推断任意输入x对应的输出值y。

上述多分类问题即M分类问题。多分类问题可以通过转化而成一系列二分类问题来解决，转化建立起来的这一系列二分类问题的两类支持向量机，针对输入x，根据这些两类支持向量机判定的结果来综合判断x的类别。不同的二分类构造对应不同的分类方法［54］。

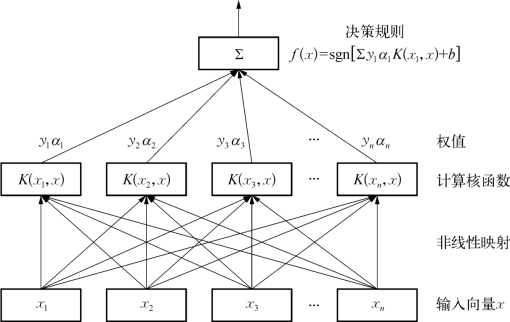
图4-38　非线性支持向量机拓扑结构

1）“一对多”分类法

“一对多”算法即第M个分类器的解是由第M类样本集合和剩下的M-1类样本集合的全体构成两类问题而得到。这样就需要构造M个分类器，然后对一个测试样本进行分类识别。

该算法的数学模型为

得到的决策函数为

式中，ω代表超平面的法向量；b代表超平面的偏置量；ξ表示松弛变量，能够降低最优分类超平面的要求；C表示惩罚因子，当C＞0时，表示对错误分类的惩罚力度。

在求解非线性问题时，对于构建的支持向量机，就是要构建从低维空间到高维空间的非线性映射，φ（xj）就是从二维空间到高维空间的一种映射，φ（xj）：R2→Rn。

2）“一对一”分类法

“一对一”分类法即将每一类和其余的M-1类中的每一类构成两类，这样可以得到个分类面，即需要构造个二类分类器把当前需要判断的这类与另一类划分开。然后根据该类与余下的各类分别建立的M-1个二类别分类器综合判断某一个输入x所归属的类别。

该算法的数学描述为

得到的决策函数为

在判定某一个输入样本的类别时，需要用上述个分类器对当前样本进行分类，若一个分类器判断此样本属于某一类，则该样本在这一类别上就获得一票，最后，获得票数最多的类别即为输入样本的所属类别。(www.daowen.com)

2.核函数与特征选择

1）核函数的选择

对于函数∫f2（x）dx＜0且f（x）≠0都能够使决策函数

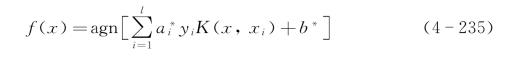
成立，则K（x，xi）便是能够将其描述为某个特征空间中的一个内积运算的核函数，K（x，xi）=φT（x）φ（xi）。式中，agn（·）是符号函数，a*是最优的拉格朗日系数，b*为阈值，i为支持向量的数目。

常见的核函数有如下几种形式：

（1）线性核函数

（2）多项式核函数

其中，向量x=［x］，xi=［xi］，d为齐次多项式核函数给定的正整数。

（3）径向基核函数

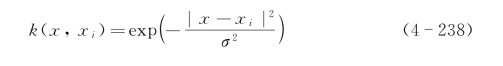
（4）Sigmoid核函数

其中，待定参数v→0且γ取很小的值是最优选择，一般情况下，v=0.000 1，γ=0。

在解决实际问题时，选取核函数的原则是将误差最小的核函数作为最优核函数。

2）特征选取方法

假设对于选择出的特征能够完全将训练样本集正确分类，即对于训练样本集，每次得到的最优超平面的经验风险相同，在此基础上，将此次所得到的最优超平面与前面所有试验所得最优超平面对于测试样本集的经验风险相比较，进而判断是否将某特征剔除。

此种假设满足序列极小化方法的基本原理，即在保持不增加经验风险的前提下，最大限度地减少特征数。在实际应用中，将样本集分为两部分，一部分用于特征选择，另一部分用于检测特征选择的效果。前者称为特征选择训练样本集，后者称为特征选择测试样本集。

特征选择极小化序列方法：①对原始的训练样本集，选择高斯径向基核函数，确定合适的参数σ，构造并求解最优化问题。②去掉原始训练样本集的第i个特征，再重复步骤①，构造出决策函数f（x），并计算与测试样本集相对应的经验风险Remp（）。③如果Remp（）≤Remp（f），则剔除第i个特征，且令f（x）=（x），Remp（）=Remp（f）；否则，第i个特征被标记。④选择新的特征，重复步骤②和步骤③，如果所有特征已被标记，停止计算［55］。

3.建立分类与匹配

也就是说，要么采用“一对多”算法，第M个分类器的解是由第M类样本集合和剩下的M-1类样本集合的全体构成两类问题而得到。然后，对于一个测试样本进行分类识别。要么采用“一对一”分类法，将每一类和其余的M-1类中的每一类构成两类，这样可以得到个分类面。然后，根据该类与余下的各类分别建立的M-1个二类别分类器综合判断某一个输入x所归属的类别［56］。

采用图4-34的人脸库数据作为算例的学习样本。将采集到的一幅动态人脸进行数据标准化，即使输入的人脸图像的范围达到预定的误差标准，因此可以消除初始权重的比例依赖问题，并提高训练速度，减少陷入局部最优状态的可能性。同时，通过标准化输入可以更方便地进行权重衰减和贝叶斯估计。数据标准化应根据实验数据的情况来选择标准化的范围，一般默认数据标准化的范围为［-1，1］。将一幅人脸图像对人脸数据库进行识别匹配，这是典型的“一对多”分类法运算。为了检测SVM分类器对人脸分类识别的实际应用效果，将分类模型对人脸图像进行分类测试。整个匹配过程可以如图4-39所示。

图4-39　“一对多”人脸库分类及匹配结果图例