基于特征脸的方法是利用主分量分析（principal component analysis，PCA）方法将人脸图像映射到低维空间来实现识别结果。该方法既能提高算法准确率，又能降低运算复杂度［24］。PCA是一种基于目标统计特性的最佳正交变换。该变换算法能够使变换后产生的新分量正交或不相关，以部分新分量表示原向量均方误差最小，具有使变换向量更趋稳定、能量更趋集中等特点，因此使得它在特征提取方面有极为重要的应用。主分量分析是多变量分析的经典技术，于1901年由Pearson引入生物理论研究，Karhunen在1974年用概率论形式来进行表示，Loéve随后发展和完善了这一理论，所以PCA有时又称为K-L变换（Karhunen-Loéve transformation）。由于该变换计算量小，能很好地用于实时处理。因此，采用PCA进行特征提取是降维处理的一种良好方案［49］。

1.主分量分析原理

众所周知，数据集所包含的属性可以从十几个到上百个不等，随着信息收集手段的发展，高达上千个属性的数据集早已司空见惯。虽然数据集的每个属性都提供了一定的信息，但其提供信息量的多少及重要性是有差异的，而且在许多情况下，属性间存在着不同程度的相关性，导致这些属性所提供的信息必然有一定的重叠。换句话说，经统计发现，异常行为往往只集中在少部分属性上，如果将算法应用在全部的属性上，不仅会耗费时间，增加计算的复杂性，还会影响数据分类的正确性。因此人们希望从数据属性中提取出主要属性，用较少的互不相关的新变量来分析问题。主分量分析正好能满足这一要求，它能够很好地处理高维数据，使得低维数据能够在二乘误差最小的意义下描述高维原始数据。

1）K-L变换

K-L变换为

反K-L变换表达为

其中，n×n变换矩阵A=［a1a2…an］，满足如下条件：

（1）ATA=AAT=I为正交矩阵，其中I为单位矩阵；列向量ai满足标准正交性，即

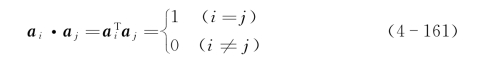
（2）ATΣxA=Λ，其中，Λ=diag［λ1λ2…λn］，λ1≥λ2≥…≥λn为Σx的特征值，且从大到小排列。

列向量ai为Σx的特征向量，即

其中，下标i表示对于x向量的统计特征量。

容易求得变换后y的均值向量和协方差矩阵为

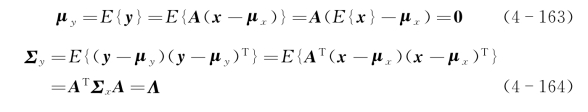
2）K-L变换性质

（1）降维估计的二乘误差最小化。

用式（4-159）的分量yi=ai·（x-μx）=（x-μx）（i=1，2，…，n）恢复x

保留1≤i≤m的yi分量，而用一些常数分量ui替代yi在m＜i≤n中的项来估计x，则估计为

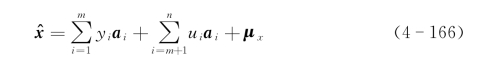
产生的误差为

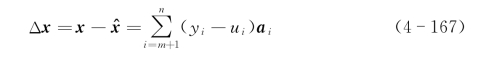
求二乘误差

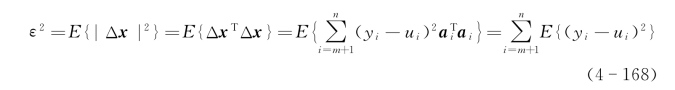
将此误差最小化

由于E｛yi｝=0，所以ui=0，估计式（4-45）简化为

其中，y1，y2，…，ym称为主分量，而被舍弃的ym+1，ym+2，…，yn称为非主分量。

将ui=0代入二乘误差式（4-168）得

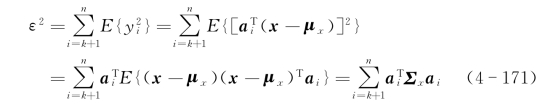
设λ1≥λ2≥…≥λn为Σx的特征值，在|a|=1的约束下，由二次型最优化可知，使aTΣxa最小化的a为最小的特征值λn对应的特征向量an，满足Σxan=λnan。

如果还要进一步降维，则舍弃第n-1个分量。以此类推，舍弃的n-m个分量对应的基向量就是较小的n-m个特征值对应的特征向量。此时

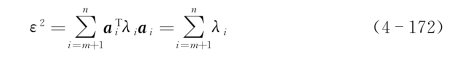
取到最小值。

由此可见，K-L变换后舍弃小特征值对应分量，估计恢复的数据在二乘误差意义下最优，其二乘误差为舍弃的特征值之和。根据这个原则建立的降维子空间，尽管去掉了一些分量，但是仍然可以用剩余的特征恢复出原有信息，保持最优的二乘误差水平。

（2）分量方差极大化。

考虑将向量x和均值μx的偏差投影到某个轴上去，轴的方向用向量a表示，其分量为

我们希望这个投影后的新分量应该尽可能多地反映原有的信息，即y的变化范围要尽可能地大，用y的方差来反映变化范围

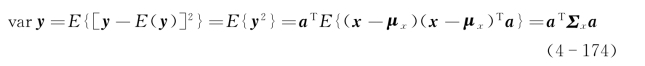
依然设λ1≥λ2≥…≥λn为Σx的特征值。

在|a|=1的约束下，由二次型最优化可知，使aTΣxa最大化的a=a1为特征值λ1对应的特征向量，满足Σxa1=λ1a1。

将x投影到垂直于a1的n-1维子空间上，可以得到n-1维的类似问题，方差最大的投影方向应该是a=a2。如果还要进一步投影，依此类推，直到投影了m次，也能够得出相同的K-L变换定义。可见，K-L变换能够最好地反映高维原始信息的降维信息，投影到主分量的降维空间上，使得各个分量的方差达到最大。

2.核主分量分析

上述PCA仅涉及在输入（数据）空间上的计算。当我们考虑另一种形式的PCA，即计算在特征空间上进行，而且它和输入空间是非线性的关系，称为线性不可分问题。这时就要运用到核主分量分析方法。尽管输入空间和特征空间存在非线性关系，即核PCA是非线性的，然而，它并不像其他形式的非线性PCA，核PCA的实现仍然可以依赖线性代数。因此我们可以将核PCA看作是一般PCA的自然扩展。

核主分量分析是引入核函数将PCA推广为核PCA（kernel principal component analysis，KPCA），首先将输入空间影射到高维特征空间，再在特征空间进行主分量分析。KPCA的内积核函数依据Mercer定理，所使用的特征空间是在该内积核定义的特征空间。KPCA直接起源于PCA，唯一的区别是在于应用空间不同。

1）核函数

核函数是在研究从一个空间向高维空间进行非线性映射φ过程中被引入的一个满足某一个特定条件的函数K（x，y）。其中，x、y为原始特征空间D中的向量。而且可以证明，存在某一空间E，K（x，y）∈E，K（x，y）就是φ（x）与φ（y）的点积（内积）。核函数也是一个对称函数。

此处所说的某一个特定条件指的是Mercer定理条件，当被引入的核函数满足Mercer定理条件时，上述结论自然成立。

Mercer定理：能够保证对称函数K（u，v）在某个特征空间中的一种内积描述，即以正的系数αk＞0展开成K（u，v）=（u）φk（v）的充分且必要条件是使得的所有g≠0，在条件

下成立。

采用不同的函数作为核函数K（u，v），可以构造实现输入空间中不同类型的非线性决策面的学习机器。

2）核函数类型

核函数包括三种类型，即多项式核函数、径向基函数和Sigmoid函数。

【类型一】多项式核函数

由

得到一个q阶多项式分类函数。式中，C为待定参数。

【类型二】径向基函数

由

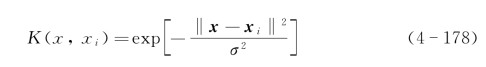
确定一个径向基函数。

由式（4-178）所得分类函数与传统径向基函数的重要区别是，这里每个基函数中心对应一个支持向量，支持向量及输出权值都是由算法自动确定的。

【类型三】Sigmoid函数

Sigmoid函数在数学上又称为双曲正切函数（hyperbolic tangent function），这是一类神经元的非线性作用函数。由

作为核函数，式中，γ、η为待定参数；tanh为双曲正切函数。

这是人工神经网络的学习算法（BP算法）。神经网络的学习是基于一组样本进行的，它包括输入和输出（可以用期望输出表示），输入和输出有多少个分量就有多少个输入和输出神经元与之对应。最初的神经网络权值（weight）和阈值（threshold）是任意给定的，学习就是逐渐调整权值和阈值使得网络的实际输出和期望输出一致。

3）核主分量

令向量φ（xi）表示输入向量xi在非线性映射φ下，将xi∈RN空间变换到高维空间RM（φ：RN→RM）特征空间中导出的像，其中，N、M分别代表原始空间RN与经过非线性映射后的高维空间RM的维数。

给定一组样本，我们有一组相应的特征向量，因此我们可以在特征空间中定义一个M×M相关矩阵，且

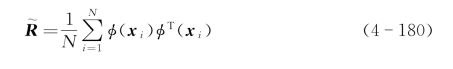
如同普通的PCA，首先要做的就是确保特征向量集合具有零均值，即

假设特征向量已经聚集于中心，则有关系

其中，为的特征值；为其对应的特征向量。

由于在≠0的情况下，满足式（4-182）的所有特征向量均落在特征向量集合｛φ（xi）生成的空间中，因此存在一组相应的系数，用它们可以写成

将式（4-180）与式（4-183）代入式（4-182）得

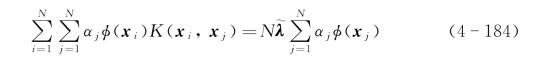(www.daowen.com)

其中，K（xi，xj）是内积核，通过特征向量由下式定义

在式（4-184）等号的两边左乘转置向量φT（xk）得

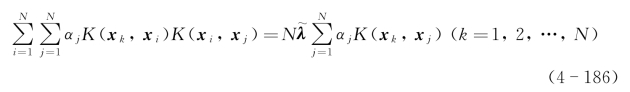
其中，K（xk，xi）=φT（xk）φ（xi）；K（xk，xj）=φT（xk）φ（xj）。

引入两个矩阵定义：

①定义N×N矩阵K为核矩阵，其第ij个元素为K（xi，xj）；②定义N×1向量α，其第j个元素为αj。

因此，可以将式（4-186）写成紧凑的矩阵形式

其中，矩阵的平方K2表示K的自身相乘。

因为式（4-187）两端均有K，围绕特征值问题的全部解同样可用更为简单的特征值问题表示为

令λ1≥λ2≥…≥λN表示核矩阵K的特征值，即

其中，是相关矩阵的第j个特征值。

从而式（4-188）变成标准形式

其中，系数向量α起到核矩阵K特征值λ对应特征向量的作用。系数向量α是归一化的，因为已经要求将相关矩阵的特征向量归一化为单位长度，即

其中，k=1，2，…，p，并假定特征值为降序排列，λp为核矩阵K的特征值的最小非零值。

利用式（4-183）和式（4-190）可以得到与式（4-191）等价的归一化条件

为了抽出主分量，需要计算特征向量在特征空间上的投影

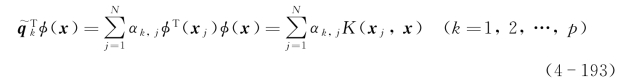
其中，向量x是“测试点”，即待测目标向量；αk，j是矩阵K第k个特征值对应的特征向量αk的第j个系数。式（4-193）的投影定义在M维特征空间RM中的非线性主分量上。

核主分量及其分析的思想如图4-29所示，其中特征空间经过变换为φ（x）与输入空间是非线性相关的。图4-29（a）和（b）所示坐标平面分别称为输入空间坐标平面和特征空间坐标平面。图4-29（a）显示输入空间上对应于特征空间线性等值线的非线性等值线簇。图4-29（b）中均匀排列的虚线表示在主特征向量上的投影为一簇常数线性等值线，特征向量用虚线箭头表示；同时显示，变换φ（x）所采用的方式为在特征空间中数据点诱导的像聚集在特征向量沿线。必须指出，此处没有在输入空间上画出特征向量的原像，这是因为它有可能不存在。

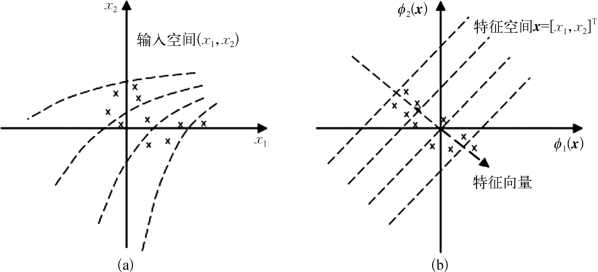
图4-29　核主分量非线性映射几何意义示意图

（a）输入空间坐标平面；（b）特征空间坐标平面

3.基于主分量分析的人脸识别

利用主分量分析原理及其方法实施对图像的识别过程大体上可以包含导入系统训练样本集、进行训练样本特征值和特征向量的计算、导入测试样本集、计算待测试图像特征向量以及分类识别等步骤。

以人脸识别为例，其本质是三维塑性物体二维投影图像的匹配问题。它的难度如下：①人脸塑性变形（如表情等）的不确定性；②人脸模式的多样性（如胡须、发型、眼镜、化妆等）；③图像获取过程中的不确定性（如光照的强度、光源方向等）。

识别人脸主要依据人脸上的特征，也就是说依据那些在不同个体之间存在的较大差异特征，而对于同一个人则存在相对比较稳定特征的度量。由于人脸变化复杂，一般来说，其特征描述和特征提取较为困难。识别过程可以分如下若干步骤。

（1）人脸图像预处理。

在对人脸图像进行特征提取和分类之前一般需要做几何归一化和灰度归一化处理。几何归一化是指根据人脸定位结果将图像中人脸变换到同一位置和同样大小。灰度归一化是指对图像进行光照补偿等处理，光照补偿能够一定程度地克服光照变化的影响而提高识别率。

（2）导入人脸训练样本。

导入人脸训练样本即读入每一个二维的人脸图像数据并转化为一维的向量，对于不同表情的人脸图像，选择一定数量的图像构成训练集。假定图像的大小是u×v（u和v分别为图像的行和列像素数），用于训练的人脸样数是n，令m=u×v，则训练集是一个m×n的矩阵。

举例来说，如取ORL人脸库（系英国剑桥大学建立的开放使用人脸数据库）中的两类图例。其中，图4-30（a）为第1类训练样本；图4-30（b）为第2类测试样本。每类均取9幅图像，每幅原始图像均具有256个灰度级［23］。

图4-30中的第l类人脸第i图像可以表示为一维向量

式中，l=1，2，3，…，c，c为人脸类数；i=1，2，3，…，nl，nl为第l类的人脸样本数；j=1，2，3，…，m，m为每个样本图像所取像素数。就ORL人脸库来说，共有40人，即c=40；每类人脸训练样本取9张照片，即i=1，2，…，9。

所谓人脸样本，即特定类（人）每幅图像能够包含表情、姿态和尺度的变化，而且姿态微变、尺度变化在20%以内等属性的图像。当每幅图像的u=112、v=92时，则m=10 304，表示第l类人脸第i图像的一维向量为

图4-30　ORL人脸库图例

（3）训练样本特征值及特征向量计算。

计算第l类的均值，即

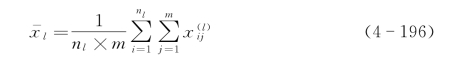
式中，表示第l类第i个样本第j个像素灰度值；由此求得的均值为平

均脸。

对第l类训练样本进行规范化后可以表达为

由训练样本组成的第l类规范化向量vl，即

此时，有第l类协方差矩阵为

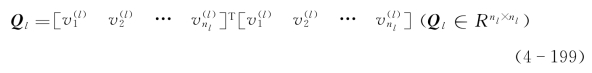
计算总均值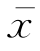，在每类样本数相等的情况下，有

称总均值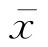为混合平均脸。

由混合平均脸进行类间规范化得类间规范化向量v，则有

其中，v（l）=（l=1，2，…，c）；由此又可获得类间协方差矩阵为

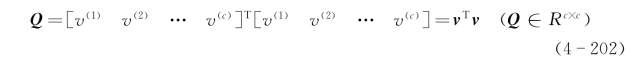
利用式（4-201）求取Q的特征值λll及其特征向量，并将其从大到小重新排列后生成特征向量

其中，λ1≥λ2≥λ3≥…，并形成一个c×c特征空间阵P，即

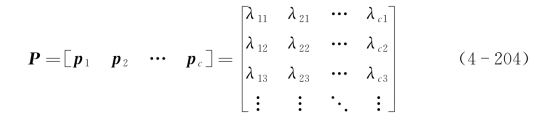
且PTP=I。

（4）对训练样本进行线性变换后投影到特征空间。

由于较大的特征值对应的特征向量包含了较多的人脸特征信息，因此可以选取前sl个较大的特征值所对应的特征向量，构成的向量空间就可以近似地表示人脸图像的主要信息。对于图像库中的nl个图像（i=1，2，…，nl）都可以向此特征空间投影，得到投影向量。

从vl=中选取前sl个较大的特征值所对应的规范化值构成新的规范化向量

及所对应的nl×c特征空间，即

所以有

因此，可以用来代表第l类人脸。

（5）导入测试样本。

假定用于测试的某人脸样本数为n，则测试集是m×n的矩阵。图4-31为取自ORL人脸库的测试样本图例，此处对某两人的人脸测试样本各取一个［23］。

（6）计算待测试样本图像特征向量。

图4-31　人脸测试样本

按照上述（3）与（4）步骤对测试样本进行测试样本图像特征值及其特征向量的计算。将测试样本投影到式（4-207）所表达的特征子空间中，此时每一幅人脸图像投影到特征子空间以后，就对应子空间中的一个点。同样，子空间中的任一点也对应一幅人脸图像。

（7）人脸识别。

把投影到子空间中的所有测试图像和训练图像一一进行比较，确定待识别样本的所属类别。如采用最近邻距离分类函数进行识别

此处的Ω即代表测试样本特征子空间，通过式（4-208）可确认测试样本中的任意一个人脸各自属于哪一类。如图4-31中的（a）和（b）所示为测试样本分别被识别为图4-30所示训练样本中的第1、2类人脸。不过，该方法对人脸图像光照和角度变化的鲁棒性较差［50］。