特征提取涉及的面很广，它和识别物体的各种物理、形态性能有很大关系，因而有各种各样的特征提取方法。图像特征可以从全局着眼，也可以从局部提取。着眼于图像局部特征的目的在于大幅度地减少识别过程的运算量，这种识别基本思想特别适用于飞行器对目标物体进行识别的快速运算。特征提取是一种基于特征量的统计模式识别方法，主要包括两大步骤：一是提取可表示模式的特征量；二是在特定的分类准则下，确定待识别目标物体所属的类。

1.决策理论方法

无论是从全局还是从局部提取特征，其统计模式识别方法最终都要归结到分类问题上来实施决策与判断。假如已经从图像中抽取出N个特征，而图像可以分为C类。那么就可以对图像的N个特征进行归类，从而决定待测目标属于C类中的哪—类。

一般把等待识别的对象称为模式，又称为测试样本，由模式（测试样本）构成N维空间中的向量x，即

令由C个模式类别ω1，ω2，…，ωc构成类别集合Ω=｛ωj｝，j=1，2，…，c；Nj表示第j个类别的匹配特征数。

物体图像识别就是要判断x是否属于Ω=｛ωj｝，以及属于Ω=｛ωj｝中的哪一类。在这个过程中要解决两个问题：一是如何抽取特征，要求特征数Nj尽可能小而且对分类判断有效；二是假设已有了代表模式的向量，如何确定它属于哪一类，这就需要依靠判别函数来实现。对于模式类别集合Ω=｛ωj｝，应有D1（x），D2（x），…，Dc（x）共c个判别函数与之相对应。图像特征识别与匹配的主程序流程如图4-16所示。

图4-16　图像特征识别主程序流程

1）线性判别函数

线性判别函数是指判别函数系由图像所有特征向量线性组合而成，即

式中，Dj（x）代表第j个类别的判别函数，βji表示第j个类别第i个特征的系数或权重，βj0为第j个类别的常数（或称为阈值）。

在两类之间的判别界处有关系

线性判别函数又称为线性分类器。任何C类别问题都可以分解为c-1个二类别识别问题。方法是先把模式空间分为一类和其他类，如此进行下去即可。当C类中的每两类别单独设计其线性判别函数时，将总共通过c（c-1）个线性判别函数实现全部的分类。多类别问题分解成c-1个二类别识别问题时的过程如图4-17所示。

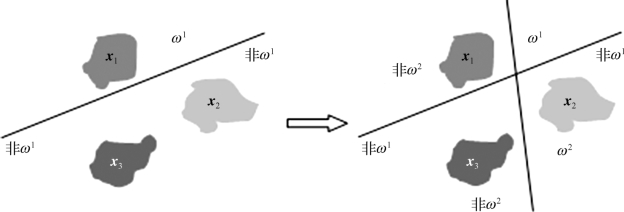
图4-17　多类问题分解成c－1个二类别问题过程示意图

该方程在二维空间R2中是直线，在三维空间R3中是平面，在n维空间Rn中则是超平面。

一般情况下，Dk（x）-Dl（x）写成如下形式：

如果Dk（x）-Dl（x）＞0，则x∈ωk；如果Dk（x）-Dl（x）＜0，则x∈ωl。

由上述可见，二类线性分类器是最简单和最基本的分解方法。分离二类的判决界由D1（x）-D2（x）=0表示。对于任何特定的输入图像模式必须判定D1（x）与D2（x）的大小。若考虑某个函数D（x）=D1（x）-D2（x），则对于一类模式D（x）为正，对于二类模式D（x）则为负，于是，只要处理与D（x）相应的一组权输入模式并判断输出符号即可进行分类。执行这种运算的分类器原理如图4-18所示。

图4-18　分类器运算原理框图

为了在线性分类器中找到合适的系数，以便使分类尽可能不出差错，基本的办法是试验法。在试验中，可以先设所有的系数为1，送进每一个模式，如果分类出错就调整系数，这个过程称为线性分类器的训练或学习。如把N维特征x和1放在一起构成y，即

令组合系数为

则线性判别函数可以改写为

考虑特征向量分别属于两个不同模式类时，存在两个训练集T1和T2。两个训练集合线性可分时，意味着测试向量y与加权向量β的内积有两种状态

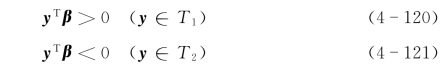
在训练过程，当分类器的输出不能满足式（4-8）与式（4-9）的条件时，可以通过“误差校正”的训练对系数进行调整。假定第一类模式yTβ不大于零，则说明系数不够大，可用加大系数的方法进行误差修正，即

对于y∈T1，若yTβ≤0，则

同理，对于y∈T2，若yTβ＞0，则

通常使用的误差修正方法有固定增量、绝对修正和部分修正规则。

（1）固定增量规则：选择α为一个因定的非负数。

（2）绝对修正规则：取α为一最小整数，它可使yTβ的值刚好大于零，即

（3）部分修正规则：

2）最小距离分类函数

在线性分类器中，有一种重要的类是把各类别样本（输入模式与特征空间）的均值向量作为各类的代表点（prototype），根据待识别样本到各类别代表点的最小距离来判别其类别。所谓最小距离分类函数，即最小距离分类器，对于c类模板将未知类别图像与其中某一类的距离最近作为判别准则。决策面是两类别均值连线的垂直平分面。

假定图像有c类，分别为ω1，ω2，…，ωc，即Ω=｛ωj｝，j=1，2，…，c；并有c个参考向量（即训练样本向量）R1，R2，…，Rc，Rj（j=1，2，…，c）与模式类ωj相联系。对于Rj最小距离分类就是把输入的新模式x分为ωj类，其分类准则就是比较x与参考模型R1，R2，…，Rc之间的距离，x与哪一个Rj最近就属于哪一类。x与Rj间的距离可表示为

由此得

由此可见，xT x与Rj无关，因此，此时的判别函数又可以表达为

可见，最小化距离|x-Rj|等价于最大化Dj（x）。换句话说，只要x∈ωj，Dj（x）即取得最大。显然Dj（x）也是一个线性函数，因此最小距离分类器也是一个线性分类器。必须指出，在最小距离分类中，遇到在决策边界上的点与相邻两类都是等距离时，这种情况分类就难以解决。此时，必须寻找新的特征，重新分类。最小距离分类函数还可以用决策区域来表示。假定有二类问题ω1和ω2，其参考向量分别对应R1和R2。

当

或

式中，r1i∈R1，即R1=［r11r12…r1N1］T；r2i∈R2，即R2=［r21　r22　…　r2N2］T。此时x∈ω1；否则，x∈ω2。

对参考向量R1与R2的样本均值连线作平分线，平分线的左、右两边分别为R1决策区域和R2决策区域，称中间为决策线（面）。对于两类情况，决策区域界为线，决策区域为两平面。对于三类情况，决策界面为超平面，决策区为半空间。对二类问题ω1和ω2分类过程的几何意义如图4-19所示。图中的μ1、μ2分别为参考向量R1与R2的样本均值。

图4-19　二类问题分类过程几何意义示意图

3）最近邻域分类函数

最近邻域分类函数法（简称最近邻域分类法）是图像识别中应用较多的一种方法，也是最重要的分类方法之一。在最小距离分类法中，是取一个标准的向量为代表。将这类问题稍微扩张一下，一类不能只取一个代表，把最小距离的概念从一个点和一个点之间的距离扩充到一个点和一组点之间的距离。这就是最近邻域分类法的基本思路。

令，c个参考向量R1，R2，…，Rc（Rj；j=1，2，…，c）分别是与类ω1，ω2，…，ωc（ωj；j=1，2，…，c）相对应的参考向量集合，即参考向量集合R为

每一个类组成的参考向量子集Rj为

则，输入特征向量x与参考特征向量Rj之间的距离可以表示为

这就是说，x与Rj之间的距离是x与参考向量子集合Rj中每一个向量的距离最小者。空间点之间距离的求取方法与最小距离分类方法中的距离求取法相同。

采用这种判别函数的图像识别，决策边界将是分段线性的。其几何意义如图4-20所示。图4-20中（a）和（b）是两种不同的分段分类顺序，（a）的决策边界要比（b）短而简捷，前者总运算时间要比后者少得多。从图4-20中可以看出，分段线性的概念较为简单，而且分段线性边界可以代表很复杂的曲线，即使本来可能是非线性边界，采用这种方法可用分段线性来近似代替。当然，如何分段及其分段顺序的选择会直接关系到分类的效果与运算时间，但是，在缺乏先验知识的前提下，测试样本的特征及其分布规律往往是未知的，因此分类过程一般是在探索中进行。

图4-20　分段线性分类几何意义示意图(www.daowen.com)

（a）分段分类顺序1；（b）分段分类顺序2

在两类判别中，ω2，当有一模式x输入识别系统时，就要分别计算其与每个类的每个点之间的距离。如图4-21所示，由于分别在k=1和k=2的情况下获得最小值，而且mink||，因此可以判定x∈。

图4-21　两类判别中未知模式判别图

4）非线性判别函数

采用线性判别函数是模式识别的基本方法，这种方法的突出优点是计算简单。但是，当两类样本分布具有多峰性质并互相交错时，简单的线性判别函数往往会带来较大的分类错误。这时需要另寻其他的解决办法。

解决上述问题存在诸多办法，其中之一就是采用分段线性判别函数法，它确定的超平面是由若干个超平面段组成的。由于它的基本组成仍然是由超平面组成的，因此，与一般超曲线（如贝叶斯决策面）相比，仍然是简单的。又由于它是由多段超平面组成的，所以它能逼近各种形状的超曲面，具有很强的适应能力。

如图4-22所示，针对三个样本分布ω1、ω2、ω3，分别给出了采用线性判别函数、分段线性判别函数和二次非线性判别函数所得到的分界面。其中，H1、H2、H3分别为线性、分段线性和二次非线性判别生成的决策面。从图中不难看出，分段线性判别函数比一般的线性判别函数错误率要小，又比一般的非线性判别函数错误率大。

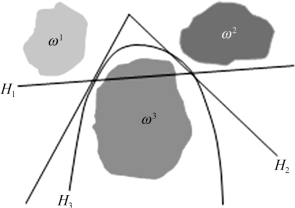
图4-22　三种判别效果示意图

根据问题的复杂性，可将判别函数从线性推广到非线性。非线性判别函数（以二次判别函数为例）可写成下列形式：

这是一个二次判别函数，通常二次判别函数的决策边界是一个超二次曲面。

为确定判别函数D（x），需要确定M个系数，则有

这是一个非常复杂的计算过程。二次判别函数的决策面包括超球面、超椭球面、超双曲面等。

对于一类（设ω1类）样本分布比较紧致成团，而另一类样本均匀地散布在其周围的两类问题，我们可用下述方法构造一个二次判别函数：

计算ω1类样本均值阵μ1和样本协方差阵Σ1

式中，N1为参考ω1类样本记录总数。

定义二次判别函数

决策规则：D（x）＞0，x∈ω1；D（x）＜0，x∈ω2。

D（x）=0在x空间确定了一个超椭球面，它的大小由式（4-138）中的K来控制，K越大，则落入超椭球外面的第一类样本点越少，因此第一类错分为第二类的概率越小，但第二类错分为第一类的概率将增大。当然还有其他多种非线性判别函数，此处不再赘述。

2.统计分类法

基于决策理论的分类方法是在没有噪声干扰的情况下进行的，此时测得的特征的确能代表模式。如果在抽取特征时存在噪声，那么被抽取的特征就有可能代表不了模式（图像），这时就要用统计法进行分类。

用统计方法对图像进行特征提取、学习和分类是研究图像识别的主要方法之一。统计方法的最基本内容之一是贝叶斯分析，其中包括贝叶斯决策方法、贝叶斯分类函数、贝叶斯估计理论、贝叶斯学习方法、贝叶斯距离等。以下重点阐述贝叶斯法则、最小错误率的贝叶斯分类法和最小风险的贝叶斯分类法。

1）贝叶斯法则

在经典概率中，贝叶斯定理已为大家所熟悉：

式中，B1，B2，…，Bn是n个互不相容的事件；P（Bi）是事件Bi的先验概率；P（A|Bi）是A在Bi已发生条件下的条件概率。贝叶斯定理说明在给定了随机事件B1，B2，…，Bn的各先验概率P（Bi）以及条件概率P（A|Bi）时，可计算出当事件A出现时，确定事件Bi出现的后验概率为P（Bi|A）。

贝叶斯公式常被运用于分类问题中。假如设x表示事件的状态或特征的随机变量，它可以表示图像的灰度或形状等，设ωi表示事件类别的离散随机变量。根据特征x对图像进行分类，就可以用如下的公式：

式中，P（ωi）是事件ωi的先验概率，它表示事件属于ωi的预先粗略了解；P（x|ωi）表示事件属于ωi类而具有x状态的条件概率；P（ωi|x）称为x条件下ωi的后验概率，它表示对事件x的状态做观察后判断属于ωi类的可能性。由式（4-140）可见，只要类别的先验概率及x的条件概率为已知，就可以得到类别的后验概率，再加上最小误差概率或最小风险法则，就可以进行统计判决分类。

2）最小错误率的贝叶斯分类法

假设有两个类别，每类有两种统计参数代表，即

ω1：P（ω1），P（x|ω1）

ω2：P（ω2），P（x|ω2）

其中，P（ω1）、P（ω2）是先验概率；P（x|ω1）、P（x|ω2）是条件概率密度函数。在噪声干扰的影响下，每个模式只能得到某一类模式的概率分布。

利用贝叶斯法则分类：若P（ω1）P（x|ω1）＞P（ω2）P（x|ω2），则分类x∈ω1；反之，P（ω1）P（x|ω1）＜P（ω2）P（x|ω2），则分类x∈ω2。在上述分类法则中，乘积P（ωi）P（x|ωi）起到了判别函数的作用。为了方便起见，在应用中，通常取乘积的对数形式

或者

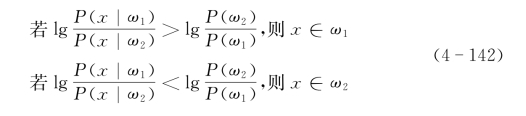
对于两类的分类问题，分界面为

设事件特征向量x的均值向量为μi，协方差矩阵为Σi，i=1，2，若P（x|ωi）是正态分布，即P（x|ωi）～N（μi，Σi），可得到其决策分界面为

式中，N为协方差矩阵Σi的行（列）数，即Σi为N×N的方阵。

如果x∈ω1，则由式（4-142）和式（4-144）得

此时两类间的决策边界是二次的。

若两个协方差矩阵相同，即Σ1=Σ2=Σ：

边界决策成为线性的，也就是说，此时最小错误率的贝叶斯分类函数就是线性判别函数。当Σ=I时，最小错误率的贝叶斯分类函数就是最小距离分类函数。

所以求两类的分类问题，若每类都是正态分布，但协方差矩阵不同，则分界就是二次函数；若N很大，求很麻烦，仍旧假设Σ1=Σ2=Σ，那将会出错，例如在图像形状识别中，就可能把球形滚珠的问题变为平面的问题，这种情况下，就要再寻求其他有效的方法予以解决。

3）最小风险的贝叶斯分类法

设x=｛x1，x2，…，xN｝=［x1x2…xN］T是随机变量，并且共有c类，即ω1，ω2，…，ωc，对于每一类模式ωi，其P（x|ωi）及P（ωi）都是已知的。以P（x|ωi）及P（ωi）为基础，一个分类器的成功条件是要在错判概率最小的条件下来完成分类任务。

定义一个决策函数D（x），当D（x）=di，表示假设x∈ωi被接受。引入损失函数L（dj，ωi），将来自ωi的输入模式x分类到ωj（做出的决策是dj）所产生的损失。

由于引入了“损失”的概念，在考虑错判所造成的损失时，就不能只根据后验概率的大小来进行分类，而必须考虑分类的结果是否使损失最小。在决策di情况下的条件期望损失为

R（di|x）也称为条件风险。

定义期望风险R为

式中，dx是特征空间中的体积元，积分在整个特征空间进行。

选择适当的决策D（x）=di（i=1，2，…，c），以使期望风险R取最小值。如果在采取每一个决策时，都使条件风险最小，则对所有的x做出决策时，其期望风险也必然最小。这种决策称为最小风险贝叶斯决策，即如果R（dk|x）=｛R（di|x）｝，则D（x）=dk（x∈ωk）。

3.图像识别过程特征分类判别相似度

有了特征向量后，就可以通过建立已知训练样本特征向量与测试目标（样本）特征向量之间的相似度来实现对测试目标的识别。如何建立特征向量相似度就是所谓的分类原则。分类原则可以根据先验知识或者事先的多次实验和现场观测来确定。

以最近邻域法为例，在众多的分类准则中，这是非参数分类的最重要方法之一。令判别相似度的类别集合为Ω=｛ωj｝，j=1，2，…，c；Nj为表明第j个类别的匹配样本数。则可以规定最近邻域类ωj的判别函数为

式中，x、y分别为训练样本与测试目标样本。

若y在第k个样本下，Gj（x，y）取到最小值，则表明此刻测试目标的测试特征向量最接近类ωj时的训练样本特征向量，即样本集合y中的某一时刻目标y∈ωj；或者说，此刻待测目标被准确识别的置信度达到最高。