所谓学习，就是利用智能识别动力与传动系统异常现象的装置对列车动力及传动系统在正常工作状态下的音响信号进行采样学习，企图建立列车动力及传动系统正常音响情况下的特征空间。对列车动力及传动系统音响信号进行采样、特征转换、建立特征空间的过程就称为对列车动力及传动系统音响信息的学习过程。学习过程在机车试验台上进行，具体步骤如下。

1.音响信号采集

由第一、第二拾音器分别采集列车动力及传动机构所发生的声音信号。这些声音信号包括启动、提速、不同转速、不同车速、减速和刹车等工况下的声音信号。拾音器通过事先设定的不同工况下的采样周期对代表不同工况的声音信号进行采集，并送入信号处理器。

2.模数转换

在信号处理器中，将声音的模拟信号转换为数字信号，交由运算模块进行处理。

3.时变信号的傅里叶变换

对声音数字信号x（t）首先进行傅里叶变换

式中，ω=2πf，单位为rad/s，将X（jω）表示成|X（jω）|ejφ（ω）的形式，即可得到|X（jω）|和φ（ω）随ω变化的曲线，分别称为x（t）的幅频特性和相频特性。式（3-111）能够获知声音信号中的频率分布信息。

4.构建列车动力机构两类训练样本

（1）对列车动力机构在多种不同工况下所发出的音响信号建立训练样本向量

式中，x1、x2分别为列车动力机构在正常工况下的幅频特性向量（1类）和列车动力机构非正常工况下的幅频特性向量（2类）训练样本向量；两类训练样本向量中的每个训练样本对应工况的采样点信息。根据这些样本可以构造出训练样本矩阵及其对应的类别样本矩阵。类别样本矩阵中的值为样本的分类类别，仅有两类，即正常工况下的音响信息和非正常工况下的音响信息，结果类别样本矩阵中的值为1或-1。

由1类和2类训练样本构成的训练样本矩阵X=［x1 x2］，与其对应的类别样本矩阵为。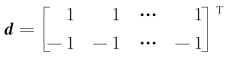

（2）求解拉格朗日乘子αi。利用公式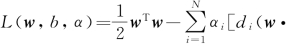xi+b）-1］，根据SVM算法和核函数中的径向基函数

进行计算。式中，σ为均方差；这里每个基函数中心对应一个支持向量，支持向量及输出值都是由算法自动确定的。

因此能够求解拉格朗日乘子αi，i=1，2，…，N与每个训练样本相对应，而且其中大部分为零，只有少数不为零的αi才对应支持向量。(www.daowen.com)

（3）求取偏置b0。利用拉格朗日乘子αi、训练样本矩阵和对应的类别样本矩阵，通过式

αi［di（w·xi+b）-1］=0　（i=1，2，…，N）

求取偏置b0。在线性可分情况下，接着可以根据公式求得w0。这样便可以得到最终分类决策函数的具体表达式。

5.构建列车传动两类训练样本

（1）对列车传动机构在多种不同工况下所发出的音响信号建立训练样本向量

式中，y1、y2分别为机车传动在正常工况下的幅频特性向量（1类）和机车传动在非正常工况下的幅频特性向量（2类）训练样本向量；两类训练样本向量中的每个训练样本对应工况的采样点信息。根据这些样本可以构造出训练样本矩阵及其对应的类别样本矩阵。类别样本矩阵中的值为样本的分类类别，因为仅有两类：正常工况下的音响信息和非正常工况下的音响信息，结果类别样本矩阵中的值为1或-1。

由1类和2类训练样本构成的训练样本矩阵为Y=［y1 y2］，与其对应的类别样本矩阵为d=。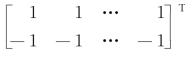

（2）求解拉格朗日乘子αi。利用公式L（w，b，α）=（w·yi+b）-1］，根据SVM算法和核函数径向基函数

式中，σ为均方差；这里每个基函数中心对应一个支持向量，支持向量及输出权值都是由算法自动确定的。

因此能够求解拉格朗日乘子αi，i=1，2，…，N与每个训练样本相对应，而且其中大部分为零，只有少数不为零的αi才对应支持向量。

（3）求取偏置b0。利用拉格朗日乘子αi、训练样本矩阵和对应的类别样本矩阵通过式

αi［di（w·yi+b）-1］=0　（i=1，2，…，N）

求取偏置b0。在线性可分情况下，接着可以根据公式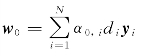求得w0。这样便可以得到最终分类决策函数的具体表达式。