早期统计学习理论所提出的VC（Vapnik-Cervonenkis）维理论为衡量预测模型的复杂度提供了有效的理论框架。但是，早期的VC维理论仅仅是建立在经验风险最小化原则基础之上，即以训练的平均误差为最小的模型作为期望的最终模型。所以，早期的统计学习理论一直停留在抽象理论和概念的探索之中。直到20世纪90年代中期，才有学者提出了基于VC维理论的支持向量机（support vector machines，SVM）算法，进一步丰富和发展了统计学习理论，使它不仅是一种理论分析工具，还是一种能够构造具有多维预测功能的预测学习算法工具，使抽象的学习理论能够转化为通用的实际预测算法。

在统计学习理论基础之上发展起来的SVM算法是一种专门研究有限样本预测的学习方法。与传统统计学相比，SVM算法并没有以传统的经验风险最小化原则作为基础，而是建立在结构风险最小化（structural rask minimization，SRM）原理基础之上，发展成为一种新型的结构化学习方法。它能很好地解决有限数量样本高维模型的构造问题，而且所构造的模型具有很好的预测性能。作为SVM算法基础的VC维理论和结构最小化原则也为进一步完善传统的统计预测方法和经验非线性预测方法提供了理论基础和统一的理论框架。

1.边界理论与VC维原理

边界理论主要包含两部分内容：一是非构造性边界理论，它可以通过基于增长函数的概念获得；二是构造性边界，它的主要问题是运用构造性概念来估计这些函数。后者的研究内容包括VC维刻画给定函数可以打散的类别数目，以及一致收敛的泛化边界。

根据样本的分布是否独立，可以分别获得具有不同性质的学习函数，可以控制学习机器之推广能力的构造性边界。

VC维描述了组成学习模型的函数集合容量，也就是说，刻画了此函数集合的学习能力。VC维越大，函数集合越大，其相应的学习能力就越强。

例如，对于二分类问题而言，令n为运用学习机器函数集合将点集以2n种方法划分为两类的最大点数目，即对于每个可能的划分，在此函数集合中均存在一个函数fα，使得此函数对其中一个类取1，而对另外一个类取-1。如图3-11所示，取二维实平面R2上的3个点，三点的名称分别为e、f、g。

设函数集合｛f（x，a）｝为一组“有向线集合”，显然，3个点e、f、g最多可以存在23种划分：（eg，f）、（ef，g）、（gf，e）、（egf，φ）、（f，eg）、（g，ef）、（e，gf）、（φ，efg）（见图3-11中从左至右、从上到下排列）。其中，二元组的第一项指示的是+1类，二元组的第二项指示的是-1类，φ表示点空集。对于任意一个划分，我们均可以在函数集合中发现一个有向线与之对应，有向线方向所指示的是+1类，反向所指示的是-1类。此时，函数集合的VC维等于3。

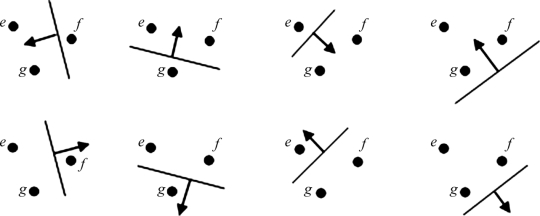
图3-11　二维平面中被有向线打散的三个点

2.推广能力边界

通过控制学习机器的推广能力能够构造适应小样本学习的归纳学习过程。由统计学习理论可知，对于任意w∈A（A是抽象参数集合），估计真实风险R（w）以至少1-η的概率满足不等式

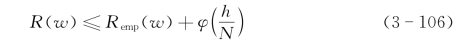
式中，Remp（w）为经验风险；）为置信风险，且

式中，N是样本个数；参数h为一个函数集合的VC维，对于线性分类器，满足

(www.daowen.com)

式中，W为训练样本向量；R为包络训练数据的最小球半径。

结构风险最小化准则的基本思想：机器为学习过程不仅要使经验风险最小，还要使VC维尽量小，这样对未来样本才会有较好的推广能力。

3.结构风险最小化归纳原理

结构风险最小化（SRM）归纳原理：不等式（3-106）中的R（w）与Remp（w）两项相互权衡，共同趋于极小，方能确保风险最小；同时，在获得学习模型经验风险最小的情况下，在VC维h值尽可能小（即置信风险尽可能小）时，学习模型的推广能力才可能大。

根据风险估计式（3-106），当训练样本数目N固定时，用以控制风险R（w）的参量有两个：经验风险Remp（w）与VC维数h。其中，经验风险Remp（w）依赖于学习机器所选定的函数f（x，w），可以通过控制w来控制经验风险；VC维数h依赖于学习机器所工作的函数集合｛f（x，w）｝，为了获得对h的控制，可以将函数集合结构化，建立h与各函数子结构之间的关系，通过对函数结构的选择来达到控制VC维h的目的。

令Sk=｛f（x，w）|w∈Ak；k=1，2，…，∞｝，且

这就是由函数嵌套子集所决定的函数集合，如图3-12所示。

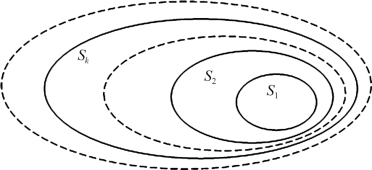
图3-12　由函数嵌套子集所决定的函数集合示意图

对｛f（x，w）｝结构化后，结构S^中的任何元素Sk拥有一个有限的VC维hk，且

所谓结构风险最小化归纳原理，就是针对给定的一组样本（x1，w1），（x2，w2），…，（xN，wN），在函数子集Sk中选择一个函数f［x，w（k）］来最小化经验风险Remp（w），同时Sk还要确保置信风险（即VC维数h）最小。

结构风险最小化归纳原理所显示出的风险与VC维数之间的统计规律如图3-

13所示。从图3-13可以看出，经验风险Remp（w）随着VC维数h的增加而递减；置信风险随着VC维数h的增加而递增；而且由VC维数h的上、下某两个参数值能够确定学习机器的欠学习和过学习区域，即h＜h-所确定的R（·）区域为欠学习区域，h＞h+所确定的R（·）区域为过学习区域。在图3-13中，真实风险边界线即为R（w）的真实曲线。

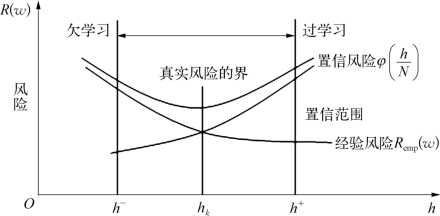
图3-13　结构风险最小化归纳原理示意图