SVM的特点如下：①支持向量是与超平面最近的样本；②支持向量尽管数量少，但却包含了分类所需的信息；③大部分训练样本不是支持向量，因此移去或减少这些样本对分类器没有影响。正是由于SVM的这些特性，针对SVM方法的理论基础及其应用已经产生了许多相关计算方法。

1.处理大数据集的SVM训练算法

与分类支持向量机相关的优化问题可以写为

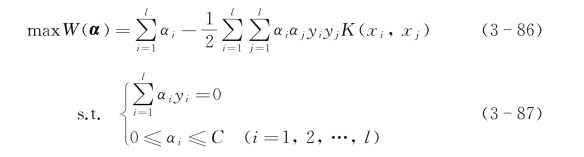
对于回归问题，线性ε-不敏感损失的问题是

SVM问题可以归结为一个二次型方程的求解。对于这种二次规划问题，经典的解法有积极方集法、对偶方法和内积算法等。当训练样本增多时，这些算法便会面临维数灾难，或者由于计算机内存的限制导致无法进行样本训练。因为，计算过程中需要计算和存储核函数矩阵，当样本点数目较大时，需要很大的内存。例如，当样本点数目超过4 000时，存储核函数矩阵需要多达128 MB的内存；其次，支持向量机在二次型寻优过程中要进行大量的矩阵运算，多数情况下，寻优算法是占用算法时间的主要部分。

针对传统求解二次规划问题速度慢等问题，目前支持向量机的训练算法一般采用循环迭代解决对偶寻优问题，即将原问题分解成为若干子问题，按照某种迭代策略，通过反复求解子问题，最终使结果收敛到原问题的最优解。根据子问题的划分和迭代策略的不同，SVM训练算法大致可分为块算法和分解法两类。

1）块算法（chunking algorithm）

在支持向量机分类算法中，由支持向量机方法得到的决策函数只与支持向量有关，与其他样本数据无关，也就是说，如果只取支持向量作为训练样本，得到的决策函数与所有样本作为训练样本得到的决策函数是一致的。因此如果事先知道哪些是支持向量，就可以仅保留与它们相对应的样本点，而从训练集中删除其他样本点。用剩下的训练集求解对偶问题就可以得到同样的决策函数。这一事实对求解大规模问题非常重要，因为支持向量数量一般很少。块模型（chunking method）就是基于这种思想而提出的用于求解海量样本数据的优化模型，即将海量样本数据集分成若干个小规模的样本集。按顺序逐个对各样本子集进行训练学习。在对每个样本子集学习时，只需要根据上个样本子集得到的支持向量以及当前的样本子集进行新的最优化计算。但我们事先并不知道究竟哪些是支持向量，通常的方法是采用启发式算法进行寻找。

换句话说，考虑到去掉拉格朗日乘子等于零的训练样本不会影响原问题的解，采用选择一部分样本构成工作样本集进行训练，剔除其中的非支持向量，并用训练结果对剩余样本进行检验，将不符合KKT条件的样本与本次结果的支持向量合并成一个新的工作样本集，然后重新训练。如此重复下去直到获得最优结果。必须指出，分块法求解规模随着支持向量数量的增加而增加，因此在支持向量数目非常大时，优化计算仍难以实现。

所谓KKT（Karush-Kuhn-Tucker）条件，即对于非线性规划的数学模型

minf（x）

s.t.　gi（x）≥0　（i=1，2，…，m）

hj（x）=0　（j=1，2，…，l）

式中，x=（x1，x2，…，xn）T∈Rn是n维向量，f、gi、hj都是Rn→Rl的映射（即自变量是n维向量，因变量是实数的函数关系），且其中至少存在一个非线性映射。

与线性规划类似，把满足约束条件的解称为可行解。若记

χ=｛x|gi（x）≥0，i=1，2，…，m，hj（x）=0，j=1，2，…，l｝则称χ为可行域。因此上述非线性规划模型可简记为

minf（x）

s.t.　x∈χ

KKT最优化条件，就是指上式的最小点x*必须满足条件

2）分解法（decomposition method）

分解法也是将大规模的二次规划问题转化成一系列小规模的二次规划求解。分解法是选择q个拉格朗日乘子αi作为优化变量（q＜N，q固定），而其他αi的值固定不变，因此分解法的子问题求解不像分块法那样，求解规模会随着支持向量数量的增加而增加，而是固定不变的。分解的基本思想是将样本数据的序号集｛1，2，…，N｝分为工作集B和非工作集B-，工作集B的大小为q，这样将大规模的二次规划问题转化成只有q个优化变量、2q个线性不等式约束、N个等式约束的小规模二次规划问题。

分解法的关键在于每次迭代过程中如何选择工作集B以及算法的收敛性问题。正因为分解法将大规模的二次规划问题转化成工作集B的大小固定为q的一系列小规模的二次规划求解，因此也称为固定工作样本集算法。必须指出，工作样本集的大小，固定在算法速度可以容忍的限度内，迭代过程选择一种合适的换入换出策略，将剩余样本中的一部分与工作样本集中的样本进行等量交换，即使支持向量的个数超过工作样本集的大小，也不改变工作样本集的规模，而只对支持向量中的一部分进行优化。

2.序贯最小优化算法

序贯最小优化算法（sequential minimal optimization，SMO）实际上是分解算法的一种特例，该算法能够避免多样本情况下的数值解不稳定和耗时长问题，同时也不需要大的矩阵存储空间，特别适用于稀疏样本，运算速度非常快。

序贯最小优化算法将分解算法推向极致，每次迭代仅优化两个点的最小子集（工作集B中只有两个样本）。该算法的优点在于两个数据点的优化问题可以获得解析解，从而不要将二次规划优化算法作为算法的一部分。它的工作集选择不是传统的最陡下降法，而是采用启发式，通过两个嵌套的循环来寻找优化的样本变量。在外循环寻找违背KKT条件的样本，然后在内循环再选择另一个样本，进行一次优化，然后再循环进行下一次优化，直到全部样本都满足优化条件为止。

具体地说，对条件=0需要在迭代中实现，意味着每步能优化的乘子最小个数为2，无论何时，一个乘子被更新，至少需要调整另一个乘子来保持条件成立。

每步SMO选择两个元素αi和αj共同优化，在其他参数固定的情况下，找到这两个元素αi和αj的最优值，并更新相应的α向量。这两个点的选择是启发式的，对这两个点的乘子的优化可以获得解析解。在求解过程，尽管需要更多的迭代才收敛，但是每次迭代仅需要很少的操作，因此算法速度得到了数量级的提高，包括收敛时间在内；同时，算法中的其他特征没有矩阵操作，不需要在内存中存储矩阵，而且容易实现。

1）两点解析解

假设选择的两个变量为α1和α2，因为α3，α4，…，αl是固定不变的，因此，式（3-

86）的优化问题等价于下面的优化问题

假设该优化问题的初始值为和，记最优解为和。可以看出，为了不违背线性约束=0，乘子的新值必须在一条直线上，即

这条线在（α1，α2）的空间，并处在0≤α1≤C、0≤α2≤C的约束中。约束目标函数到一条直线上所得到的一维问题有解析解。

用该算法首先计算，然后利用它计算。根据不等式约束0≤α1≤C、0≤α2≤C和线性约束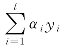=0，在的可行值上提供了一个更为严格的约束

(www.daowen.com)

如果y1≠y2，则

如果y1=y2，则

使用f（x）表示在学习的特定阶段值α和b所决定的当前假设，即

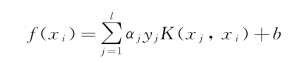
并令

这是对训练点x1或x2上的函数的目标分类的差别值，即使训练点能够被正确分类，这个值Ei仍有可能很大。另一个量是目标函数在对角线上的二次导数，可表示为k，则有

式中，Φ（·）表示原始空间到特征空间的映射。

定理：当α1和α2允许改变时，式（3-90）目标函数的最大值可以通过计算下面的量得到

剪辑它来实现约束U≤αnew2≤V

式中，E1、E2由式（3-98）给出，k由式（3-97）给出，U、V由式（3-94）或式（3-95）给出。进一步，可以从得到，则有

因此，（）是式（3-90）的最优解。

2）启发式选择算法

为了提高收敛速度，可以根据点在求解过程中的贡献来选择其中两个点作为子集优化目标函数。如果实现选择策略所需要的计算量小于节省下来的迭代所需的计算量，就表明在收敛过程中获得收益。选择的停止条件能指示出哪些点更易于对收敛做出更大贡献。

SMO使用两个条件来选择两个活动点，确保目标函数在优化过程中有更大的增长。用两个单独的启发式算法来选择第一个点和第二个点。

（1）第一个选择的启发式算法。

第一个点x1从最违反KKT条件的那些点中选取。算法的外循环浏览数据集寻找违反KKT条件的点，并使用任意一个点来更新。当这样的点找到时，用第二个选择的启发式方式选择第二个点，更新各自乘子的值。然后，外循环重新寻找违反KKT条件的点。为了提高寻找违反KKT条件的点的机会，外循环浏览那些对应参数满足0＜αi＜C的点，这意味着它的值不在可行区域的边界上，只有当这些点在特定的容忍等级满足KKT条件，在整个数据集上的完整循环运算才算结束，然后进入下一个数据集。

（2）第二个选择的启发式算法。

第二个点x2的选择要按这样的方式：在α1、α2上的更新引起更大的变化，使得对偶目标产生大的增长。为了不必进行过多的计算就能找到一个好的点，一种快速的启发式方法是选择最大化量|E1-E2|的点为x2。如果E1是正的，则SMO选择一个具有最小误差E2的样例x2；如果E1是负的，则SMO选择一个具有最大误差E2的样例x2。内存保留数据集中每个不在边界上的点的误差，可以减少计算量。如果这个选择没有在对偶目标上产生大的增长，SMO则会轮流尝试每个非边界点。从各自列表的随机位置开始遍历每个非边界点和整个数据集的循环，这样就不会在两者中任何一个开始的时候就引入偏置。

对于回归，SMO算法可以从式（3-90）给出的优化问题再次更新α1和α2。四个独立问题的编程与两个参数的符号有关。α2的区间由下式给出：

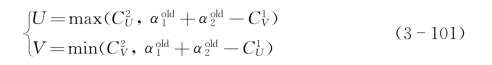
这里四个问题的参数有不同的设置，如表3-1所示。

表3-1　参数设置

使用f（x）表示在学习的特定阶段，α和b所决定的当前假设，并令

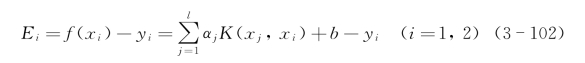
Ei是训练点x1或x2上的函数输出值与目标值的差别。

定理：当α1和α2在包含两个值的特定象限中允许改变时，优化式（3-86）目标函数的最大值，可以通过计算下面的量得到

剪辑它来实现约束U≤≤V，则有

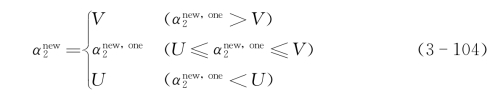
这里符号函数sgn（·）的值由选择的象限决定。E1、E2由式（3-102）给出，k由式（3-97）给出，U、V由式（3-101）给出。进一步，可以从得到，则有