通常情况下，设计工程师都是以选择等厚度钢板为基本元素进行零部件或是整体结构设计的。而在利用安全系数来评估一个结构的设计优劣时，往往根据结构中的最大应力值是否大于设计需要的安全应力值为标准。如果降低结构中的某个零件的应力值，除了在结构上采取一些措施进行局部加强外，最直接的办法是将该零件的厚度加大。这种办法可以将该零件中的应力值降低，但是增加的厚度只有很小部分对降低应力起到了作用，所增加厚度的大部分都是对结构强度没有贡献的和无用的，这无形中增大了机构的重量。因此，最优化的设计是使结构各个零件的每一部分都发挥其最大的效能，这也将是结构轻量化的极限目标。变厚度钢板技术的发展和应用正是利用了这一原理，根据零件对整体结构的强度、刚度以及安全的贡献和需要来确定其尺寸。

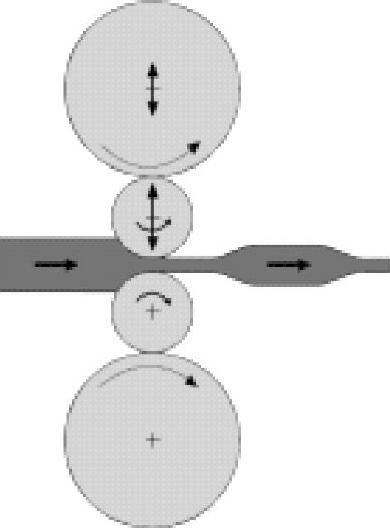
图11-172 TRB轧制原理

1.等强度原理

零部件在机构中承受载荷时，在机构中的应力场往往是连续而不均匀。如何使结构内部应力场分布达到均衡，从而实现结构的最佳设计才是所要追求的目标。可以从一个简单截面简支梁的受力分析来理解受力件的等强度应力状态与其断面尺寸的关系。

如图11-173所示悬臂梁，若梁的截面采用高度为H，宽度为B的矩形截面，按强度条件

式中M（X）——弯曲力矩（N·M），且

M（X）＝F·X （11-8）

F——悬臂梁所施加载荷（N）；

W——抗弯截面模量（MM³），且

B——梁的截面宽度（MM）；

H——梁的截面高度（MM）。

[σ]——梁的许用应力（N／MM²）。(www.daowen.com)

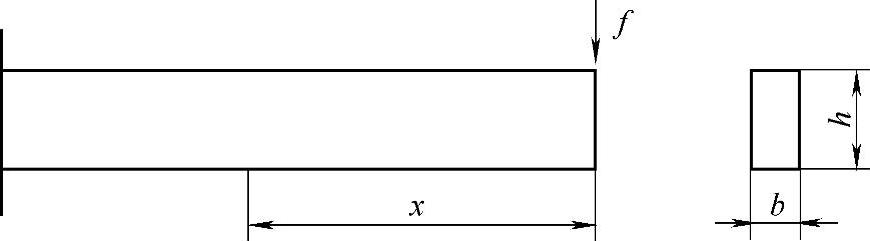
图11-173 简单断面悬臂梁受力图示

如果认为梁的宽度是不变的，将式（11-7）和式（11-8）代入式（11-9）并简化，可得悬臂梁在等强度条件下，梁的截面高度沿长度方向的函数关系

式中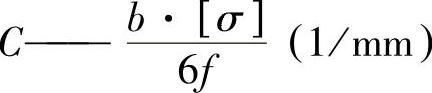，为常数。

式（11-10）说明，如果保持悬臂梁在每一个截面上的最大应力为恒值，且不考虑悬臂梁在结构宽度的变化，梁的高度在长度方向上应为2次曲线关系，如图11-174所示。这一理论描述为汽车车身等结构件的设计提供了依据，尽管大部分的结构件宽度是变化的，但至少说明在零件的长度方向材料厚度的连续变化是实施结构轻量化的最佳设计，这也直观地说明变厚度钢板的利用将比拼焊板更能使结构轻量的原因。

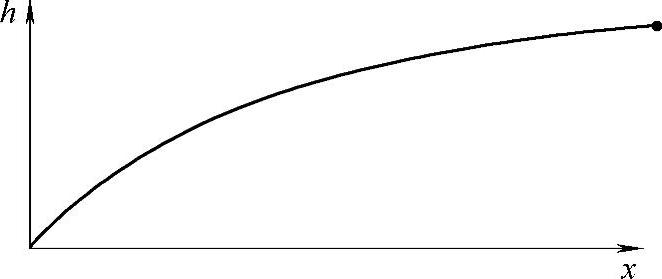
图11-174 等强度时悬臂梁截面高度沿长度方向的变化

2.过渡曲线的设计

汽车车身零件的形状直接与其承担载荷和性能贡献相关。变厚度钢板的过渡区设计既要体现该零件的载荷及性能承担，又要兼顾轧机压下系统的调节能力，同时也影响到冲压生产线和模具设计。在分析用轧制方法获得过渡区特点的基础上，提出以下4种类型的过渡区曲线，如图11-175所示，其中图A所示为双弧主导型过渡曲线；图B所示为直线主导型过渡曲线；图C所示为凹弧主导型过渡曲线；图D所示为幂函数主导型过渡曲线，考虑等强度的原理二次幂函数曲线。图A和图C适应于较短的过渡区，而图B和图D适应于较长的过渡区。

选取过渡曲线要考虑轧制、冲压、产品服役条件等多方面因素，尺寸较长且变化均匀和缓的过渡区，有利于均匀承载和冲压成形，钢板的表面几乎看不到厚度变化的痕迹。尺寸较短、厚度变化剧烈的过渡区可以节省更多的金属，适用于产品服役中受到载荷有急剧变化的场合，过渡区太短则轧制和冲压成形的难度都加大，其过渡区长度的最小极限值与轧辊直径有关。

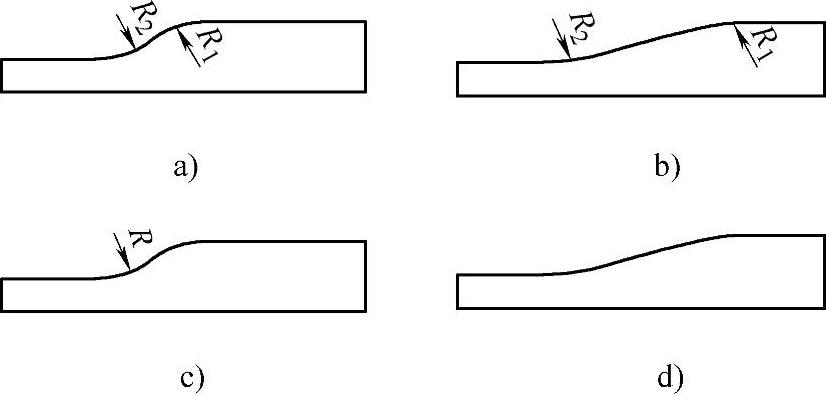
图11-175 变厚度钢板的过渡区

A）双弧主导型 B）直线主导型 C）凹弧主导型 D）幂函数主导型