1.曲率回弹量
设加载时和加载后工件中性层弯曲半径分别为R1和R2,曲率回弹量ΔK与加载弯矩M的关系为

式中I——工件型材截面惯性矩;
E——工件材料弹性模量。
拉弯时为使截面内应力尽量均匀一致,最小拉伸应变量应为

则距离中性层Y处的切向总应变为

在塑性范围内,应力应变关系为

将式(10-58)代入式(10-59),得

式中REL——工件材料的下屈服强度;
D——工件材料应变刚模量,应为应变函数,近似取为常数。
等效截面和截面应力,如图10-49所示。加载弯矩M为:
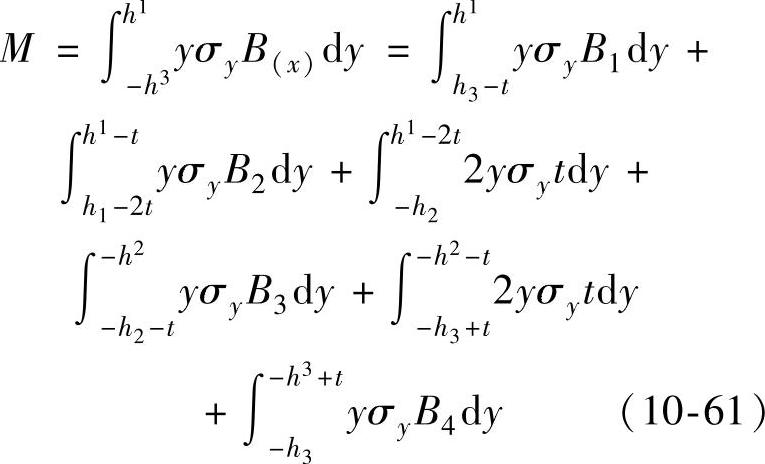
化简式(10-61),得。
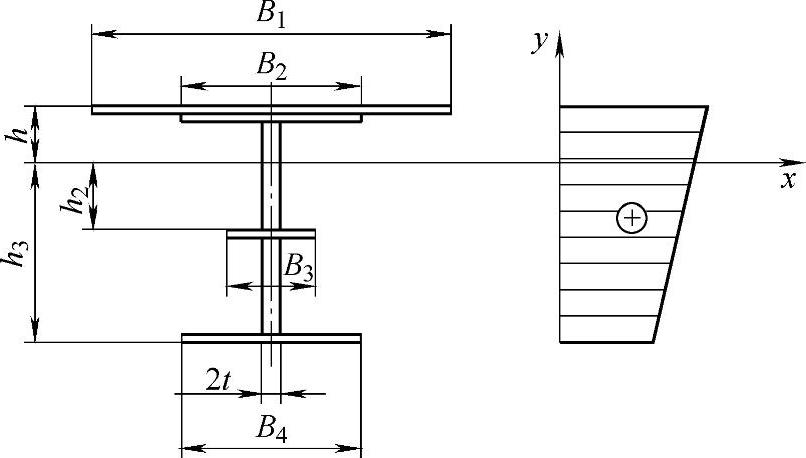
图10-49 等效截面及截面应力

式中U、V——型材截面尺寸系数。
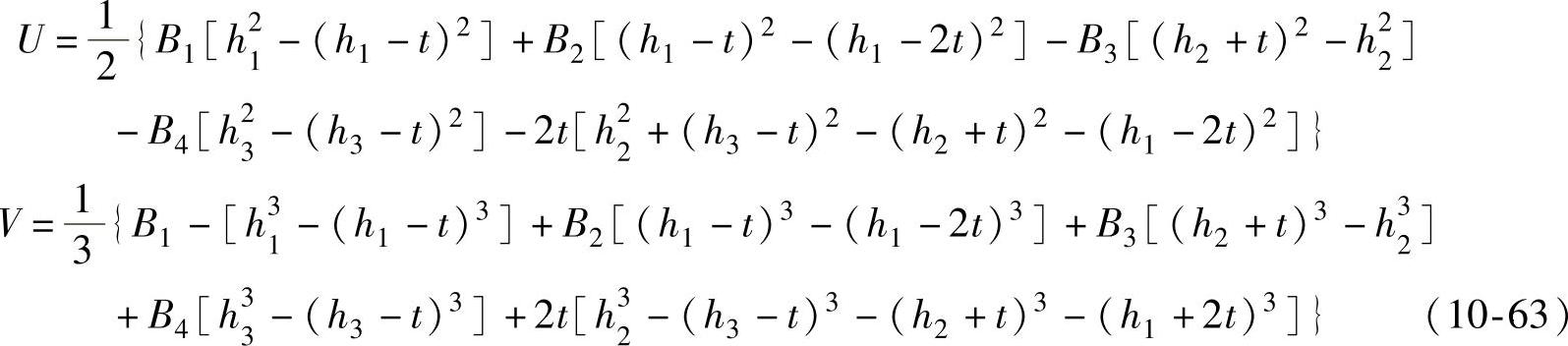
得到曲率回弹量

它与制件的材料性能、截面形状及弯曲半径都有关。(www.daowen.com)
因曲率回弹量也可表达为如下形式

故将式(10-64)代入式(10-65),整理得
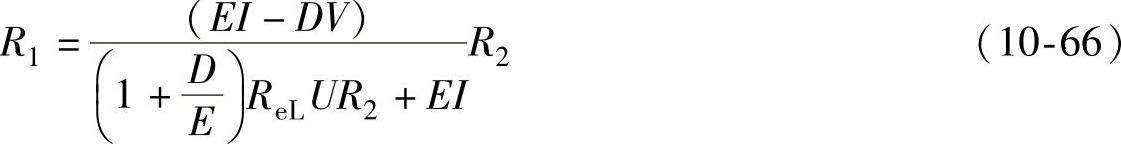
2.角度回弹量
拉弯时角度的回弹量包括两部分:弯矩卸去后产生的角回弹ΔαW和拉力卸去后产生的角回弹ΔαL,即,
Δα=ΔαW+ΔαL(10-67)
(1)卸弯矩后的角度回弹量 设R1和R2分别为加载时和加载后工件中性层弯曲半径,设α1和α2分别为弯矩加载和卸载时的中性层弯曲角度,因加卸载弯矩前后中性层长度不变,所以有
R1·α1=R2·α2 (10-68)
由式(10-65)得

将式(10-69)代入式(10-68),得

则弯矩卸去后产生的角回弹为
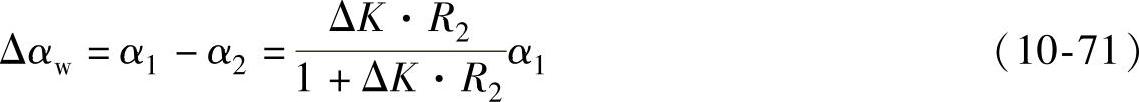
(2)卸拉力后的角度回弹量 当拉力卸去后,型材截面各层纤维绕曲率中心成比例缩短,中性层处缩短量引起的角度变化即为拉力卸去后产生的角回弹。
由式(10-60)得中性层处的拉应力

因为

则有拉力卸去后产生的角回弹为

将式(10-71)和式(10-74)代入式(10-67),得总的角度回弹量
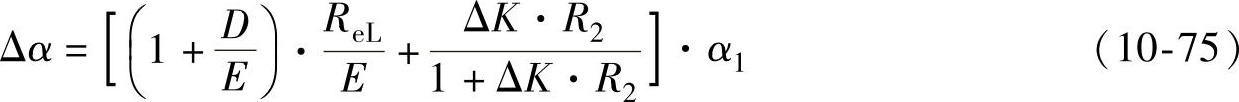
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







