型材因其良好的机械性能在航空及汽车工业上应用广泛。型材拉弯是指在型材预拉伸至材料屈服极限时,加载弯曲并同时保持一定的轴向拉力,使之进入模具型槽内而成形的弯曲过程。在弯曲的同时施加轴向拉力以克服内侧的起皱及改善截面内的应力分布,减少回弹,提高其外形精度。
型材拉弯回弹量的控制是型材拉弯要解决的主要问题之一。在拉弯零件生产过程中,拉弯模外形是依据拉弯零件的形状设计得到的。即使在技术规范所允许的残余应变规定下尽量增大轴向拉力,但由于型材零件的相对弯曲半径较大,仍存在一定的回弹量。拉弯成形后的曲率仍偏小,因而拉弯后仍需要进行校形。
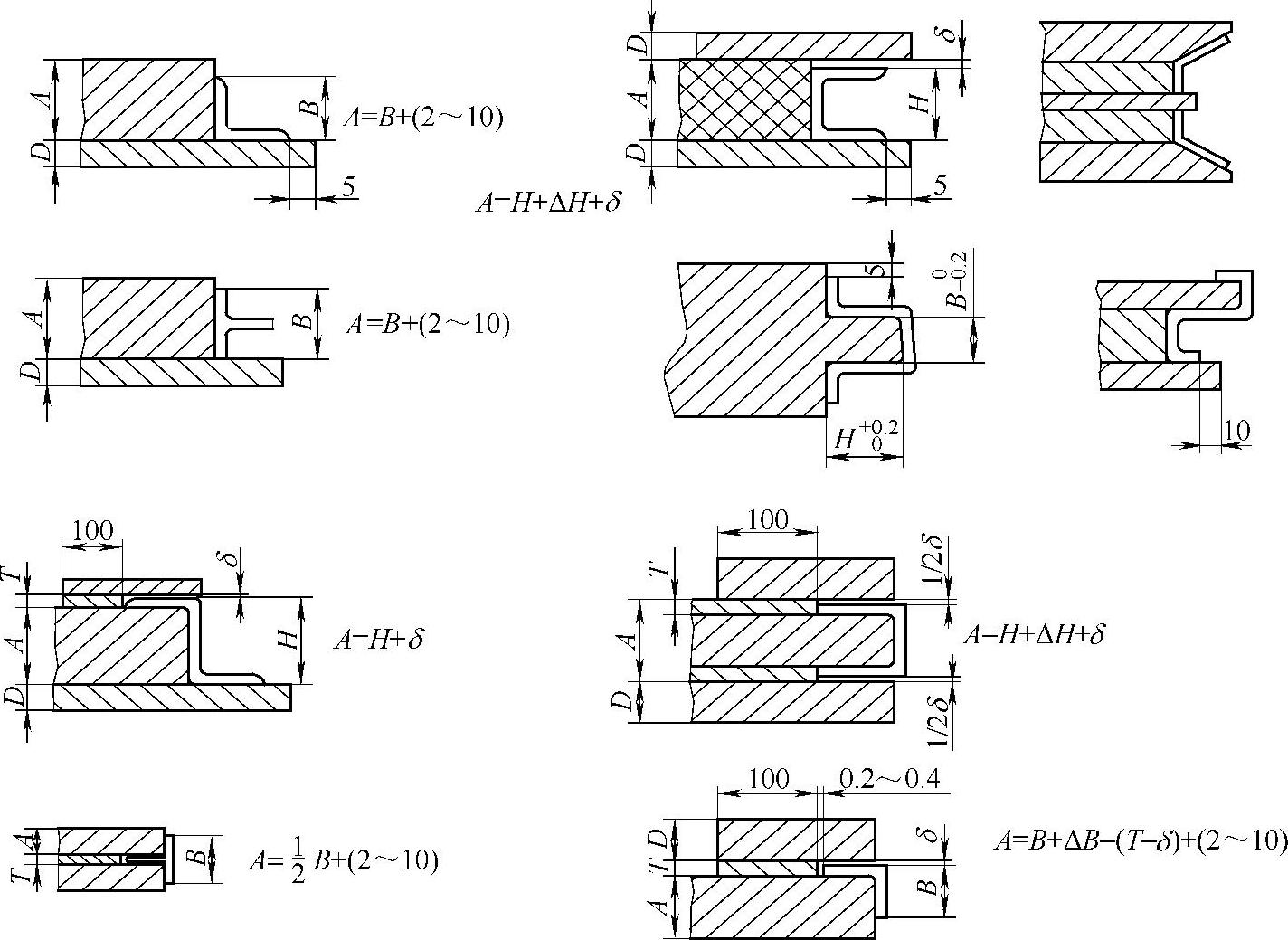
图10-34 拉弯模剖面形状
因此设计拉弯模时,应在依据10.4.1节分析的基础上对拉弯件轮廓形状进行修正得到拉弯模轮廓形状,以保证型材在卸载后具有更合理的轮廓形状和校形余量。
拉弯模型面修正具体算法如下。
1)根据拉弯件的数学模型抽取出轮廓曲线,按照等参数方式在提取出的轮廓曲线上布点I=0,1,2,…,N。计算拉弯件轮廓曲线上点P处的曲率半径。
而在UG中,有5种点的分布方式,即等弧长、等参数、几何级数、弦公差、弧长增量。
等弧长方式即是在指定的曲线上按等弧长的方式分布点,不能突显曲率的变化对点的分布密度的影响。
等参数方式即是在指定的曲线上基于曲线的特征或参数的分布点,在这种方式下,曲线曲率大的地方点的分布密,曲率小的地方点的分布稀。
几何级数方式即是在指定的曲线上基于几何比例参数来控制点的分布。
弦公差方式是在指定的曲线上基于弦公差基数值来控制点的分布,这种方式不能事先指定分布点的具体个数,点的数目完全由输入的基数值来决定。
弧长增量方式是在指定的曲线上按照等增量的情况,在曲线上顺序生成相应的点。点的数目由增量设定,增量越大点的数目越多,反之越少,并且生成的点不能完全覆盖曲线。
由于在UG中曲率梳的密度是按照等参数的方式设定的,因此通过曲率梳得到的曲率值反映的是相应等参数点处的曲率。同时这种方式也能反映曲线不同曲率处的点的稀疏,综合考虑上述情况,在截面曲线上采用等参数的方式布点。
2)修正各点的曲率半径的计算。由(10-45)式计算点PI处曲率修正量(www.daowen.com)
ΔRI=KRI (10-49)
则修正后拉弯模在点PI的曲率半径为
RI′=RI-ΔRI (10-50)
3)模具型面逐点修正计算。这里采用圆弧样条来表示模具轮廓形状,是由于圆弧样条具有几何不变性。所谓几何不变性,就是图形不随座标选择而变化。圆弧样条采用了局部坐标系,每段圆弧的圆心和半径是几何不变量,故其图形不随坐标系的选择而变化。而三次样条函数虽然方法简单易行,拟合效果好,而且可保证二阶连续,但它存在一个根本的问题,就是其图形不具有几何不变性。通常三次样条函数是几何可变的,它的图形会随着坐标的选择而变化。因此,改变了坐标系,就相当于在新的坐标系下重新给出了一组新的型值点,因而生成的样条曲线与原来的样条曲线不完全重合(虽然在型值点处是重合的)。这样,就有可能产生不协调。此外,圆弧样条还可以克服大挠度问题,并且圆弧样条的计算比其他样条曲线简单、准确。选取轮廓曲线的起始点矢量→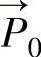 ,计算该点的法矢量→N
,计算该点的法矢量→N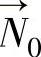 ,设修正后模具轮廓上对应点矢量为
,设修正后模具轮廓上对应点矢量为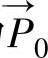 (如图10-35所示),曲率中心矢量为→O
(如图10-35所示),曲率中心矢量为→O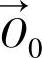 。则有
。则有
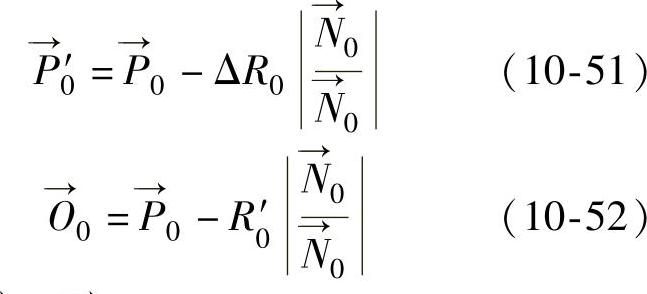
当已知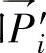 和
和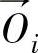 (I=0,1,2.…N),并当点足够密时,
(I=0,1,2.…N),并当点足够密时,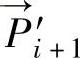 可近似通过等式
可近似通过等式
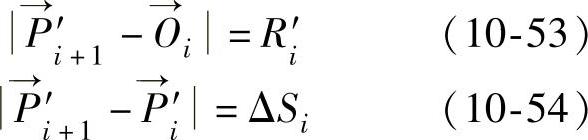
求出(见图10-36)。其中,ΔSI为→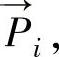
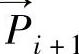 两点之间的弧长。
两点之间的弧长。
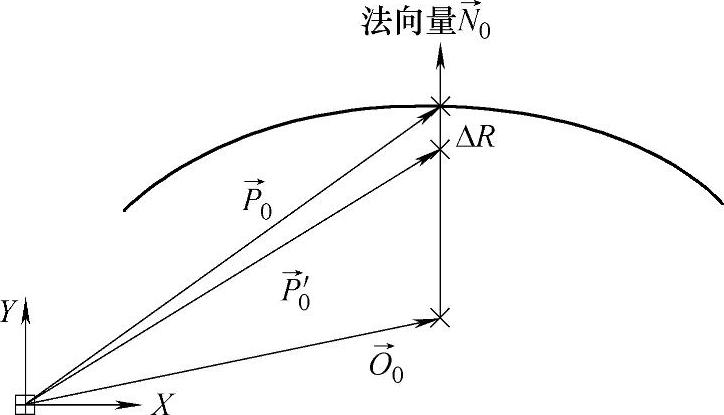
图10-35 模具初始修正点计算示意图
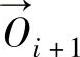 的计算方法为
的计算方法为
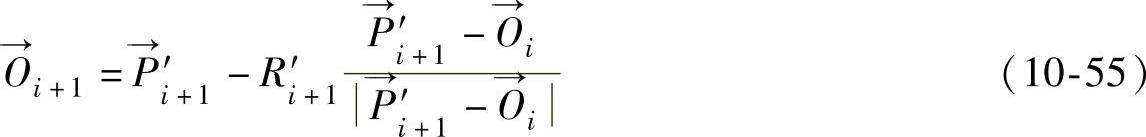
该算法得到的模具轮廓曲线都是连续的,在点PI处可保证切线连续,曲率为分段常数。可通过拉弯件轮廓曲线上布点的密度来控制模具轮廓曲线上曲率分段的多少。点分布的越密,模具轮廓曲线上曲率分段越多,其拟合出的曲线的误差就越小。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





