1.纯弯曲回弹机理

（1）弯曲阶段 板料在弯曲过程中，随着外加弯矩的逐步增大，弯曲变形程度随之增大。从弹性弯曲变形到塑性弯曲变形的过程可以分为两个阶段。

1）弹性弯曲阶段。板料在弯曲过程中，外层的材料受到拉伸变形，内层的材料受到压缩变形。沿板料厚度以应力中性层（应力为零的层次）为界将板料划分为拉伸变形区和压缩变形区，如图10-7A所示。板料中任意一点可以近似认为处于线性应力状态。应力沿板料厚度呈线性分布。

图10-7 弹性弯曲和弹塑性弯曲时的应力分布

板料外层（或内层）材料的应变ε_W。（或ε_N。）仅为自变量即相对弯曲半径R／T的函数：

一般采用相对弯曲半径（R／T）表示弯曲过程的变形程度。相对弯曲至越小，弯曲变形程度则越大。弹性弯曲阶段的特点是：相对弯曲半径很大，当外加弯矩卸掉后，毛料立即恢复原来的平直状态。

2）弹塑性弯曲阶段 随着弯矩的继续增大，外层与内层材料首先进入塑性变形状态，而后塑性变形区逐步往应力中性层扩展，沿板料厚度以应力达到条件屈服强度σ₀.2的层次为界线划分为弹性变形区与塑性变形区（见图10-7B），板料中任意一点仍近似认为处于线性应力状态。采用折线型近似实际应力曲线时，沿板料厚度应力呈折线分布。

弹塑性弯曲阶段的特点是：当外加弯矩卸掉之后，塑性变形区的材料会保存残余变形（见图10-8），但是由于弹性变形区材料的弹性恢复以及塑性变形区材料弹性变形部分的弹性恢复，而引起较大的回弹现象，这就是生产中产生回弹现象的内因。

（2）板料弯曲回弹半径的一般表达式 弯曲零件在弯曲过程中，其横剖面上不但存在塑性变形区，而且还存在弹性变形区，如图10-9所示。此外，塑性变形区内材料的塑性变形中还包含着弹性变形。因此，当弯矩卸掉之后，零件的弯曲半径比卸载前增大，而弯角减小，这就是回弹现象。

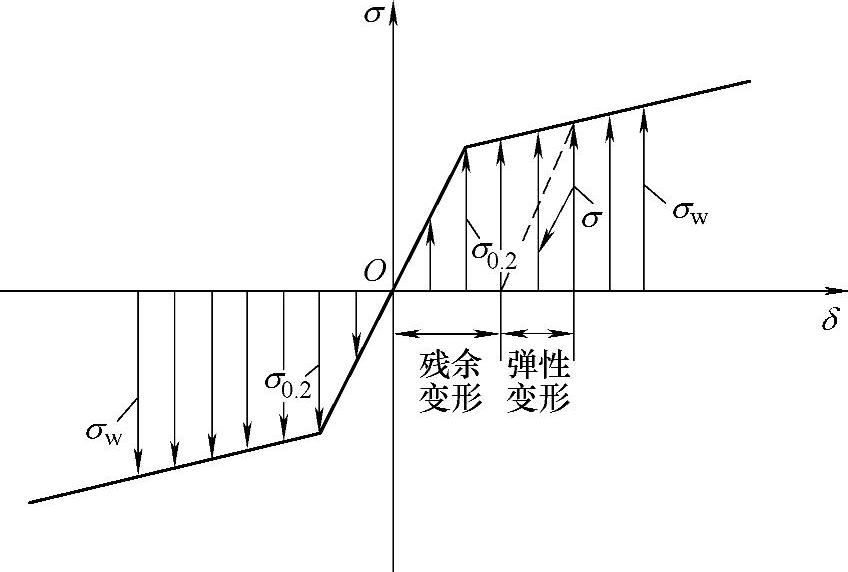
图10-8 卸载

设图10-9所示是从板料弯曲零件中取的一段.回弹前弯角为α_Q，回弹后减少为α_K，内层材料的弯曲半径在回弹前为R_NQ，回弹后增大为R_NH，回弹前内层材料的长度为L_N，外层材料长度为L_W。内外层材料原来受压缩，卸载后伸长。对于相对弯曲半径较大的零件，伸长应变δ_N≈ε_N，故伸长量为δ_N L_N。外层材料原来受拉伸，卸载后收缩应变δ_W≈ε_W，故收缩量为δ_WL_W，板料的厚度仍为T。

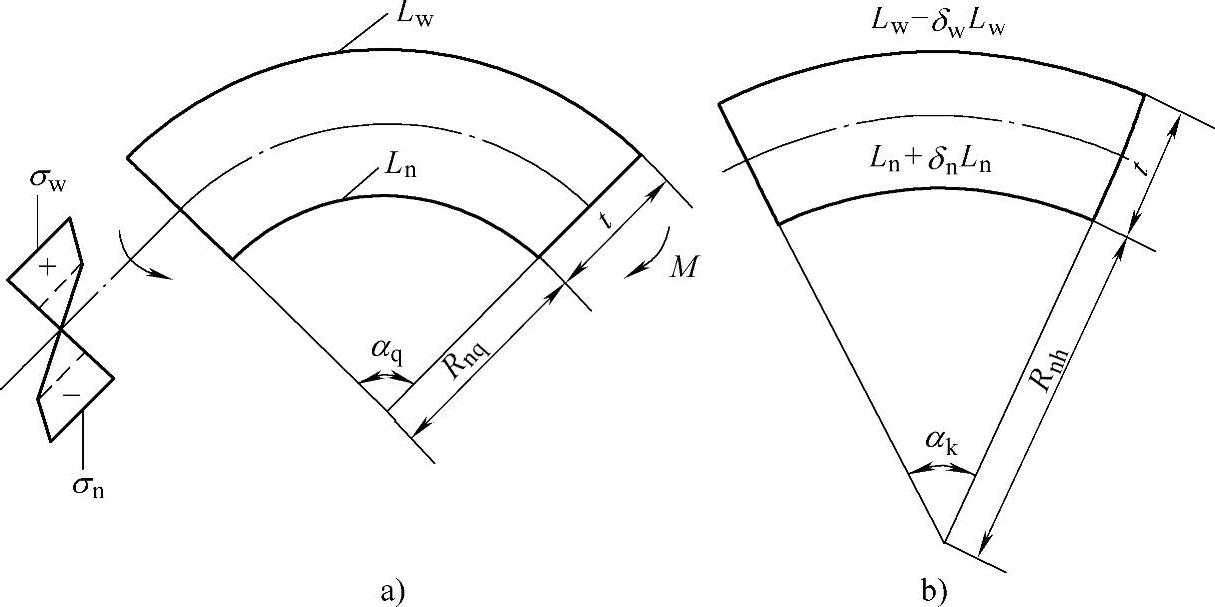
图10-9 板料回弹前与回弹后几何尺寸比较

A）回弹前 B）回弹后

在推导回弹半径与回弹角的表达式之前，为简化数学上的运算（在保证必要的准确度前提下）与分析问题方便起见，作如下基本假设。

1）平截面假设。即沿纵向任意横截面在塑性弯曲前为平面，塑性弯曲后仍为平面。

2）零件的塑性弯曲属于纯弯曲。即不考虑剪力的影响。

由图10-9A所示可得外层材料与内层材料在回弹前的弧长分别为

L_W＝（R_NQ＋T）·A_Q （10-19）

L_N＝R_NQ·AQ （10-20）

两式相除得

由图10-9B所示可得外层材料与内层材料在回弹后的弧长分别为

L_W（1－ε_W）＝（R_NQ＋T）·A_H （10-22）

L_W（1＋ε_N）＝R_NQ·A_H （10-23）两式相除得：

L（R_NH＋T）（1＋ε_N）

令式（10-21）与式（10-24）相等，得

（R_NH＋T）（1＋ε_N）

即

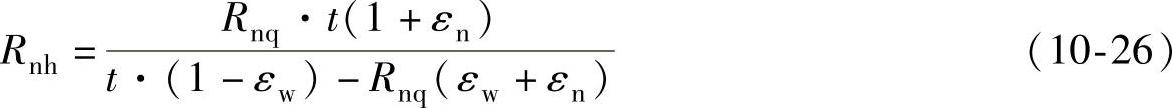
根据卸载定理，弹性收缩应变ε_W与弹性拉伸应变ε_N应和外层材料与内层材料所受的应力σ_W与σ_N成正比关系（见图10-10）。在不考虑残余应力的情况下，此关系式按胡克定律为

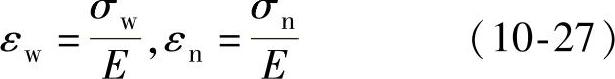
将上式代入式（10-26）可得

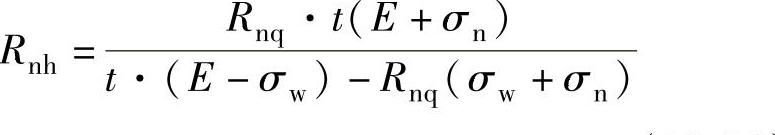
（10-28）

由于E≫σ_W，E≫σ_N，故式（10-28）中E^－σ_W≈E，E＋σ_N≈E。式（10-28）经简化换算可得内层材料回弹后的曲率半径R_NH为

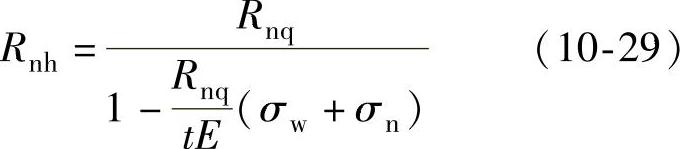
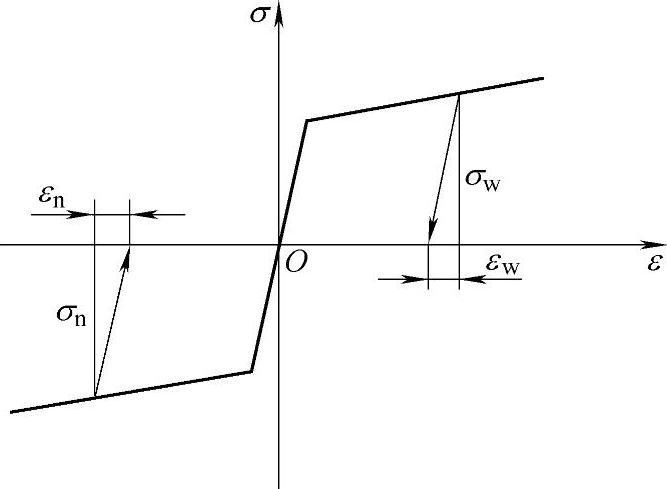
图10-10 卸载时应力与回弹应变的关系

以上经换算可得回弹半径ΔR的表达式为

式中E——板料的弹性模量。

由式（10-30）可见：

1）相对弯曲半径越大，回弹半径越大，这是由于弹性变形区所占的范围增大所致。

2）回弹半径尚决定于材料的机械性能，而材料的机械性能由材料的种类与供应状态而定。

3）在一定的相对弯曲半径情况下，弯角的变化与回弹半径无关。这是由于前者代表弯曲变形区域的大小，而后者代表一定的弯曲变形程度。

上述虽然给出了计算板料回弹量的公式，但实际运用时会存在一定的误差，主要原因是：在其他条件不变的前提下，回弹量与板料厚度成反比。而在上述分析过程中，我们假定板料的厚度是不变的。但在弯曲成形过程中，板料的厚度会发生变化，即中性层以外的厚度由于弯曲拉应力减少，而中性层以内的厚度却由于弯曲压应力增加。由于弯曲变形时中性层有内移的趋势，厚度减小区大于厚度增加区，从而导致板料的总厚度减少，因此运用时会有一定的误差。(www.daowen.com)

2.型材拉弯回弹分析

型材拉弯与板料压弯过程中应力分布不同。在板料压弯过程中，压缩变形区的内层材料应力为压应力（见图10-11）。在型材拉弯过程中，由于轴向拉力的作用，使压缩变形区的压应力改变为拉应力（见图10-12）。

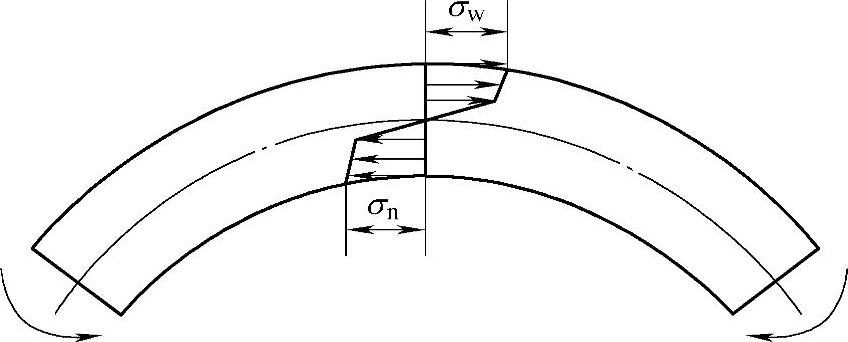
图10-11 板料弯曲时的应力分布

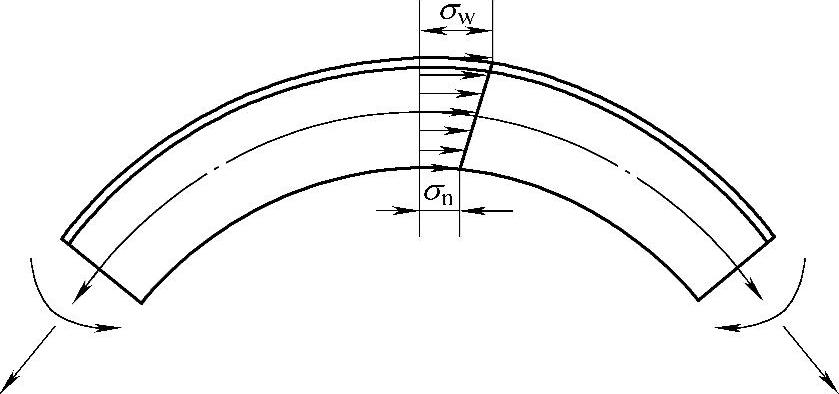
图10-12 型材拉弯时的应力分布

则拉弯型材回弹半径由板料压弯回弹半径式（10-30）变换得

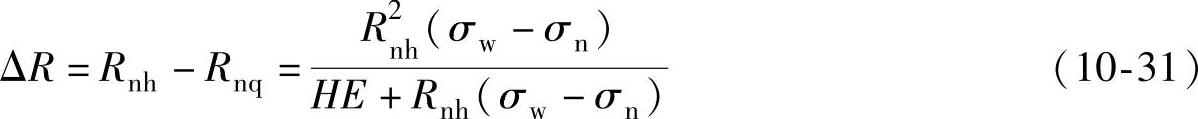
由式（10-31）可见，影响拉弯型材回弹半径率的主要因素是材料的机械性能E、剖面尺寸H、曲率半径R_NH以及内外层材料的应力差σ_W－σ_N。前两个与选定的型材有关。因此生产中影响回弹半径的主要因素是R_NH与σ_W－σ_N，其中内层材料回弹后的曲率半径R_NH决定于拉弯零件的外形，应力差σ_W－σ_N则决定于型材两端的轴向拉力与弯矩的加载方式和轴向拉力的大小。

综上所述，如果在选择合适的加载方式与轴向拉力的同时，拉弯模的外形又考虑了回弹量，则可控制拉弯零件在拉弯成形后具有合理的校形余量。

为进一步简化回弹半径计算式，使理论公式应用于生产成为可能性，作以下假设。

1）平截面假设——认为型材的任意截面在拉弯前是平面，拉弯后仍为平面。

2）型材的弯曲属于纯弯曲，亦即不考虑剪力的影响。

3）采用折线型近似实际应力应变曲线，并认为在使用范围内拉伸曲线与压缩曲线相同。

现以等曲率收边拉弯角材为例，说明加载方式与加载过程以及回弹量与轴向拉力的解析计算方法。

目前生产中通常采用的一次拉弯的加载方式是先拉伸后弯曲再拉伸，其加载过程为：首先对其两端施加轴向预拉力，使横剖面上的应力达到屈服极限：而后在预拉力不变的条件下施加弯矩使之贴模，最后补加轴向拉力。总拉力的大小以使受摩擦影响最大的剖面（处于拉弯模对称中心线的横剖面）上其内层材料的应力达到拉伸屈服极限为准。在预拉力的作用下，既保证了沿型材轴向任何横截面上的应力呈线性分布，又同时减少了外层与内层材料的应力差，从而使沿型材轴向各段均减少了回弹量。

型材在预加轴向拉力作用下，剖面上的应力分布是均匀的，外层材料与内层材料的应力σ_W1与σ_N1为 （见图10-13B）

σ_W1＝σN1＝σ0.2（10-32）

弯曲之后，外层材料的拉应力σ_W1沿实际应力曲线增大为σ_W2，而内层材料的拉应力σ_N1却沿着实际应力曲线减少为σ_N2，即

σ_W2＞σ0.2；σN2＜σ0.2 （10-33）

补拉轴向拉力之后，外层材料的拉应力σ_W2仍沿实际应力曲线继续增大为σ_W3，而内层材料的应力σ_N2又沿实际应力曲线增大，至达到条件屈服强度σ₀.2为止，即

σ_W3＝σW，σN3＝σN＝σ0.2 （10-34）

型材在拉弯模对称中心线处的横剖面上，在补加轴向拉力之后的应力呈线性分布。设与应力中性层距离为Y的材料所受的应力为σ_Y（见图5-13A），则

σ_Y＝σ₀.2^＋ΔσY＝σ₀.2＋Δδ

≈σ₀.2^＋D（ε_Y^－ε0.2）（10-35）式中D——应变刚模量。

取一微段，其中性层长度为L₀，由几何关系（见图5-13C）可得距离中性层Y处材料的应变为

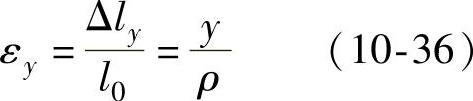
式中ρ——中性层曲率半径。

按照胡克定律

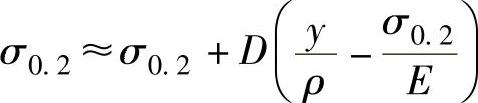
（10-37）

设应力中性层与内层材料的间距为A（见图5-13C），由几何关系

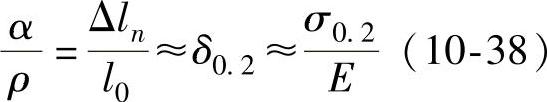
得：

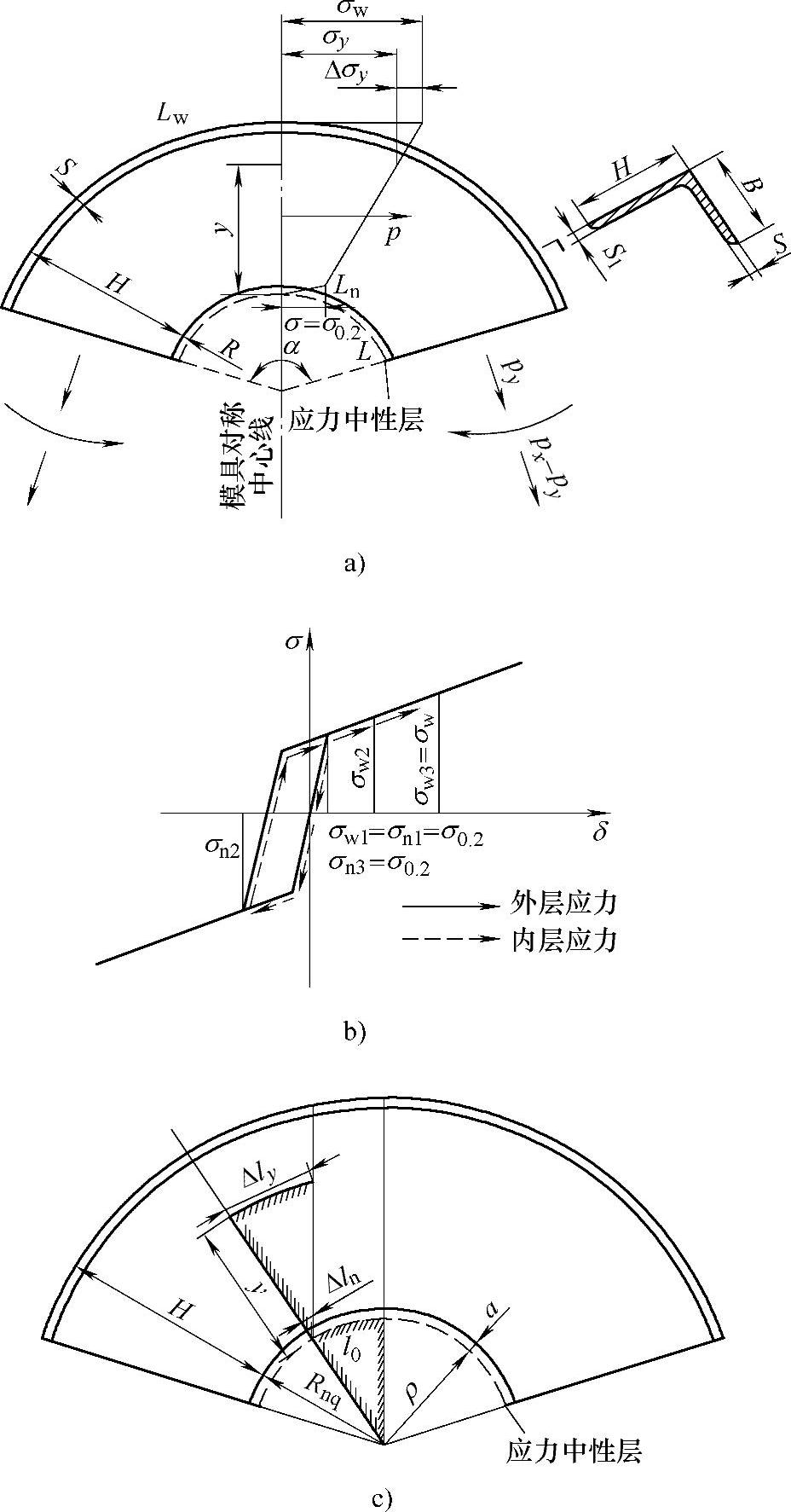
图10-13 等曲率收边角型材拉弯过程的应力与应变分布

由边界条件，当Y＝A时，σ_Y＝σ_N＝σ₀.2，可得

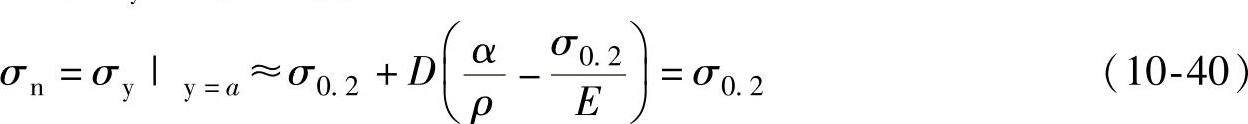
当Y＝A＋H时，σ_Y＝σ_W，可得

因此，外层材料与内层材料的应力差σ_W＝σ_N为

由几何关系可知（见图5-13C）

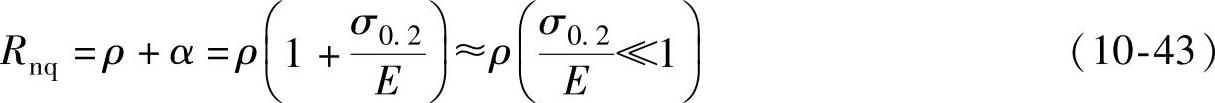
故得：

则可得：

式中K——回弹系数。

由式（10-45）可得，型材拉弯回弹系数K主要取决于材料的机械性能（D与E），也决定于材料的种类与供应状态。