1.开路电压法

开路电压法是最简单的测量方法，主要根据电池组开路电压判断SOC的大小。由电池的工作特性可知，电池组的开路电压和电池的剩余容量存在着一定的对应关系。某动力电池组的电压与容量的对应关系如图4-8所示。随着电池放电容量的增加，电池的开路电压降低。由此，可以根据一定的充放电倍率时电池组的开路电压和SOC的对应曲线，通过测量电池组开路电压的大小，采用插值法估算出电池SOC的值。

该方法简单易行，但由于不同充放电倍率时电池组的电压不一致，因此，在电流波动比较大的场合，这种方式的计量将失去意义。另外，不同应用工况下电池组的内阻大小不一样，导致了同样充放电倍率下不同时期的电池组的电压不一致，使得该测量方式的测量精度很低。同时，温度对电池组的放电平台影响也较大，因此，单靠电压来估算SOC的方法难以满足实际需求。

还有一种是在电池组充放电状态转换时通过电压对电池组的容量进行估算，根据经验模型，在充放电状态改变时用模型来估计容量。相当于引入电池的内阻进行校正，比普通的电压和容量相对应的方式精确度稍高一些。

开路电压法对单体电池的估计要优于电池组，当电池组中出现单体电池不均衡，会导致电池组的可用容量降低时电压仍很高，因此，该方法不适合个体差异大的电池组。

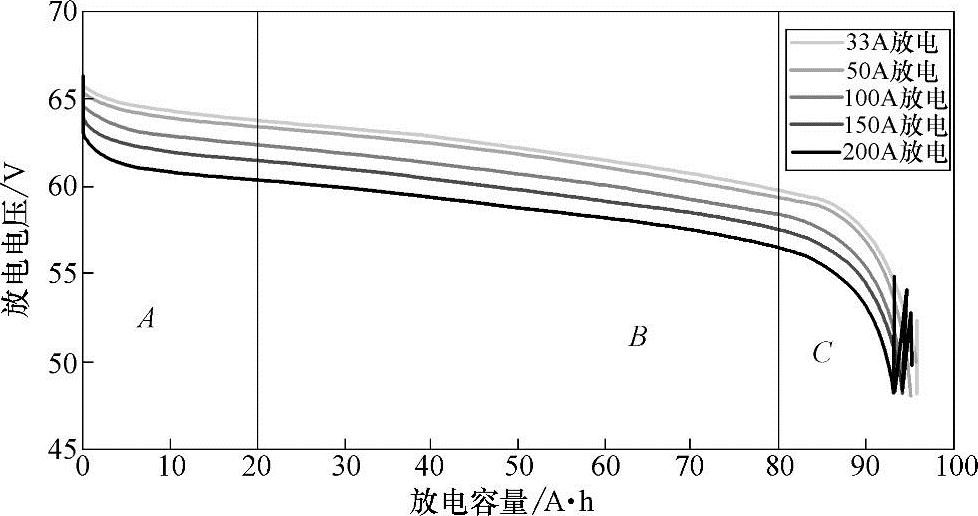
图4-8 某动力电池组电压与容量的对应关系

2.容量积分法

容量积分法（电流积分法）是通过对单位时间内，流入流出电池组的电流进行累积，从而获得电池组每一轮放电能够放出的电量，确定电池SOC的变化。

电流积分法存在着一定的误差，多次循环之后会出现一些误差积累，使该误差越来越大，因此需要校正。目前的方法大多利用电池组电压来校正因电流积分导致的累积误差。通过电池组放电到放电终止电压时，无论SOC值为多少都置为0，这样可以避免长时间积分的累积误差。有的在电池组静态时采用电压法来校正SOC，而在工作时采用电流积分的方法。然而由于电压和容量的对应关系，受到了温度、放电电流、电池组均衡性的影响，因此，仅仅通过电压法校正SOC的精度仍然较低，需要作进一步的改进。

3.电池内阻法

电池内阻有交流内阻（常称交流阻抗）和直流内阻之分，它们都与SOC有密切关系。电池交流阻抗为电池电压与电流之间的传递函数，是一个复数变量，表示电池对交流电的反抗能力，要用交流阻抗仪来测量。电池交流阻抗受温度影响大，是对电池处于静置后的开路状态，还是对电池在充放电过程中进行交流阻抗测量，存在争议，所以很少在实车测量中使用。

直流内阻表示电池对直流电的反抗能力，等于在同一很短的时间段内，电池电压变化量与电流变化量的比值。实际测量中，将电池从开路状态开始恒流充电或放电，相同时间里负载电压和开路电压的差值除以电流值就是直流内阻。直流内阻随SOC的变化规律如图4-9所示。(www.daowen.com)

直流内阻的大小受计算时间段影响，若时间段短于10ms，只有欧姆内阻能够检测到；若时间段较长，内阻将变得复杂。准确测量电池单体内阻比较困难，这是直流内阻法的缺点。在某些电池管理系统中，内阻法与容量积分法组合使用来提高SOC估算的精度。

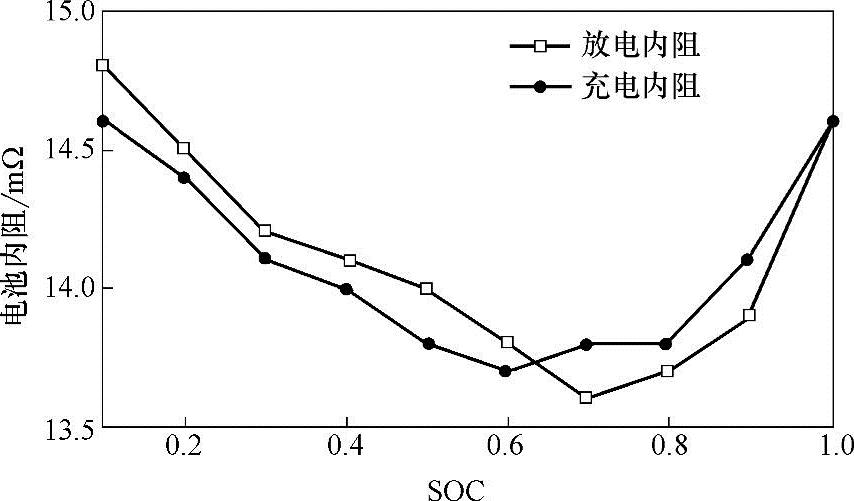
图4-9 某电池直流内阻随SOC的变化规律

4.模糊逻辑推理和神经网络法

模糊逻辑推理和神经网络是人工智能领域的两个分支，模糊逻辑接近人的形象思维方式，擅长定性分析和推理，具有较强的自然语言处理能力；神经网络采用分布式存储信息，具有很好的自组织、自学习能力。它们共同的特点是均采用并行处理结构，可从系统的输入、输出样本中获得系统输入、输出关系。电池是高度非线性的系统，可利用模糊推理和神经网络的并行结构和学习能力估算SOC。

采用神经网络预测SOC的典型结构如图4-10所示。网络结构为多输入单输出的三层前馈网络。输入量为电流、电压、温度、充放电容量、内阻等，输出量为SOC值。中间层神经元个数取决于问题的复杂程度及分析精度。神经网络输入变量的选择是否合适，变量数量是否恰当，直接影响模型的准确性和计算量。神经网络法适用于各种电池，其缺点是需要大量的参考数据进行训练，估计误差受训练数据和训练方法的影响很大。

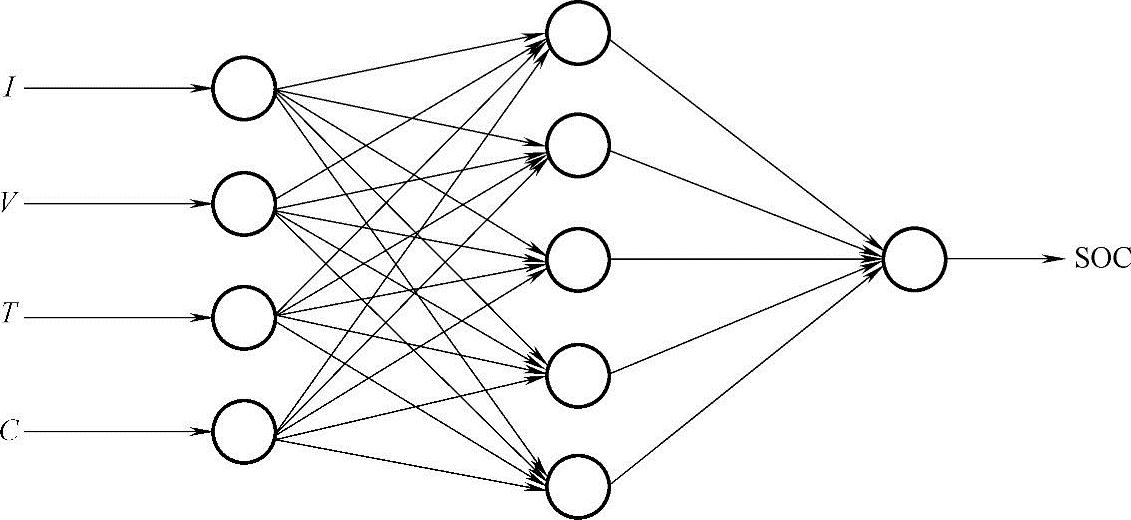
图4-10 估算SOC神经网络结构图

5.卡尔曼滤波法

卡尔曼滤波理论的核心思想是对动力系统的状态做出最小方差意义上的最优估算。卡尔曼滤波法应用于电池SOC估算，电池被称为动力系统，SOC是系统的一个内部状态。

卡尔曼滤波方法适用于各种电池，与其他方法相比，尤其适合于电流波动比较剧烈的混合动力汽车电池SOC的估计。该方法的缺点是要求电池SOC估计精度越高，电池模型越复杂，涉及矩阵运算的量越大，工程上越难以实现，且该方法对于温度、自放电率以及放电倍率对容量的影响考虑得不够全面。