简单来说，深隧是深埋地下的重力流排水管道，非满流状态下隧道内的空气流动以及与隧道内水流的关系与普通浅层排水管道一样。

重力流污水管通常设计为非满流，类似于明渠流，并且在充满度d／D（水流深度d与排水管道直径D 的比值）为0.5～0.75时设计最小速度超过0.75m／s。最小设计流速是防止固体从废水中沉积，并提高废水的新鲜空气夹带能力。充分混合的充氧废水可以保持比较高的溶解氧，可以阻止厌氧环境下硫化氢（H2S）的产生。但在湍流条件下，会促使废水中溶解态的H2S向污水管道顶部空间释放，在产硫酸菌的作用下生成硫酸，腐蚀管道内壁，或最终会泄漏到大气环境中，影响周边环境。

为排水管道，尤其是大尺寸干管，设置完善的通风系统，可以阻止H2S的产生，缓解管道内壁腐蚀现象，还可以避免臭气对周边环境的影响。通风量如何确定、通风设备如何选择以及除臭工艺如何选择等问题，都需要对排水管道内空气动力学及其影响因素有充分了解。

目前的研究成果表明，排水管道内由于水的流动而导致的空气流动受多种因素影响，包括被空气占据的管道上部空间、水的流速、水面宽度、排水系统内外温差、水深等，及其相互之间的作用。尽管对管道空气动力学有了诸多初步研究成果，水环境研究基金会（WERF）发布的报告指出：“虽然废水导致的臭味和腐蚀性非常重要，但废水收集系统通风设计仅仅在污水处理专业人员中被简单地理解。”排水管道内空气动力学研究成果仍有缺陷，需要继续做更多的研究工作来完善。

4.5.2.1　深隧系统空气流动影响因素

排水系统通风模型方面仍然有多个问题需要解决，目前还没有一套完整的、得到业内人士一致肯定的空气动力学理论供工程人员参考。下面对深隧内空气流动有影响的几种因素做一个概述，希望对深隧通风系统的设计工作有一定的引导。

（1）水流摩擦阻力的拖拽作用

圆形深隧内水流移动产生的摩擦拖拽力，视觉上可以使管道上部空间的空气向与水流相同流动的方向移动。在气—液界面处产生的摩擦力，气—液两相接触面积越大，摩擦力就越大。对于圆形深隧管道，半满流时产生的摩擦力最大。由摩擦力引起的诱导空气流量是在评估排水干管顶部空间内空气的自然流动建模时的主要参数。

当水从跌水竖井落下时，在跌落过程中形成液滴，增加气—液接触面积，因此，更多的空气被携带在下跌水流中，导致跌水竖井下游隧道上部空气压力的增加，以及增加臭味释放到系统外部周边大气的潜在可能性。

（2）水流速度和深度的变化

水深和水流速度的变化会产生不同的瞬时条件，比如进入大型深隧的水流的增加，将引起水位上升，原本被空气占据的空间被增加的水流替换，这部分置换空气将被来水“挤出”深隧系统，这个过程在缺乏通风系统的深隧中更加明显。在通风系统比较完善的深隧管道中，这种空气置换通常小于风机的排风量。相反，等深隧内水流减小时，水位将降低，需要额外的空气来置换水位下降而空余出来的空间，这就需要通风系统能及时补充足够的置换空气量。

（3）空气温度差及其引起的浮力

深隧深埋于地下，基本可以保持相对恒定的温度，比如13℃。在寒冷的季节，外部空气温度比较低，外部空气密度比深隧管道内的空气密度要大，如果深隧系统有显著的空气流通通道，在这个密度差形成的浮力作用下，深隧内比较轻的气体会外溢到周边空气，这种效应称为烟囱效应。

在最早期的一些排水设计中，有些研究建议使用可以产生诱导气流的烟囱作为通风系统的核心构筑物，来改善排水管道系统的自然通风特性。在排水管道内的空气和外部空气之间存在足够温差的情况下，大而高的烟囱可以产生足够优良的空气流通。然而，近年建造的深隧系统，往往接入深隧的浅层支管数量比较少，加上深隧系统各种人孔、检查孔等基本完全封闭，形成了“封闭”系统。因此，由于浮力和温差引起的深隧内空气流动，几乎无法泄漏到外界。不管怎样，由于深隧系统缺乏明显的泄漏点，这个封闭系统倾向于加重由气液界面摩擦力形成的诱导气流带来的系统内局部空气增压现象。

（4）风力传导

如果排水系统设有通风烟囱，烟囱口附近的风速比较大的时候，由于空气快速流动在烟囱口附近形成局部低压区，烟囱内外的气压差会造成排水管道内空气被“抽出”管道进入大气，这种现象称为风力传导。

为了防止隧道内臭气对大气的污染，现代排水隧道系统一般不会设置正面朝上的通风烟囱来专门将排水管道内空气排入大气。通风管会安装单向阀，仅允许新鲜空气进入排水管道，而阻止排水管道内臭气释放到大气中。

（5）通风瓶颈位

通风瓶颈主要由局部管道内水位升高或管道本身标高布置引起，比如倒虹吸管，局部瓶颈位会阻碍排水干管顶部空间的空气流通。这些瓶颈可以减小管道顶部空气流动断面面积，甚至在管道全断面完全阻塞管道内空气流动。由于瓶颈位的阻碍，上游水流带来的诱导空气在该处聚集，形成管道顶部气压升高，会导致臭气逸散进入周边大气。典型排水管道中瓶颈位附近的空气流通过程如图4-41所示。

（6）机械通风

排水隧道的机械通风可以通过风机来从隧道顶部空间抽取空气，目的是保持隧道顶部空间内相对大气环境而言有一个轻微的负压环境。机械通风技术手段可以有效地在局部空间受限或受控的“密闭”排水隧道系统中实现良好的通风环境。美国已在大管径污水干管上进行了抽气试验，表明：①使用风机可以在排水隧道顶部空间内产生负压；②负压力可能在干管内很长距离内得到保持，特别是在检查孔等密闭性相对较好，且没有主要的横向支管接入的情况下。

为了避免深隧内臭气对周边环境的影响，排水隧道通按照“密闭”系统设计，因此，系统内外温度温差、烟囱效应和风力传导等因素对空气流动的影响远远小于水流摩擦阻力和通风瓶颈位的影响。因此，对于“密闭”的非满流排水隧道或截污工况下运作的复合型隧道，各种影响因素对于新建深隧系统的通风设施设计的重要性，总结如下：

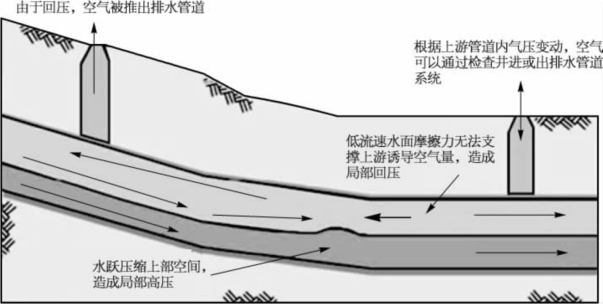
图4-41　典型污水系统空气流动示意图

①水流摩擦阻力的拖拽作用是设计的主要控制因素。

②污水流速和深度的变化不如摩擦阻力显著，不应该在通风设计中起主要作用。

③系统内外温差以及引起的烟囱效应可忽略不计，但该压力差可作为主隧内需要保持的最大负压（机械通风需要保持的系统内外气压）。

④风力引导对污水隧道通风影响不大。

⑤特定位置设置通风瓶颈位，比如主隧内设置风挡，以控制臭气在隧道内的运动方向。

对于复合型深隧或排涝深隧，暴雨期间入流量非常大，有可能形成严重浪涌现象。浪涌过程中，通风系统设计着重考虑瞬间水位升高导致的大量置换空气所需要的通风量，需要根据深隧断面尺寸、水位升高速率等因素，确认浪涌过程中深隧系统最大的排风量。一般需要设置专门的通风口来处理这种特殊工况下的巨大排放量需求。

4.5.2.2　排水管道空气动力学模型

排水管道中气体运动的最主要动力是在气液交界处水流与空气间的摩擦力。通常认为，在水面处的空气流速最大且接近水流速度，而距离水面越远，空气流速越小。排水管顶部空间的空气压力的变化主要受空气流速、空气量以及整个下水道的气密性的影响。当井盖有操作孔或有多条支管接入时，排水管道内的空气压力自然比较低。这种情况与带有孔洞的通风管中的气压变化相似。密封井盖或连接支管较少时，易导致压力增加，并使高压区在管道系统内扩展距离达数千米。

目前在北美，针对排水管道内空气流动的研究已经有了多个研究成果和计算流体动力模型，主流的动力学模型有三个：①1981年，Pescod和Price的经验推导模型。这个模型来自一个300mm 直径的实验室重力管试验结果。②2004年，Edwini-Bonsu和Steffler建立的计算流体动力模型（computational fluids dynamic，CFD）。该模型的建立基于二维的管道几何断面形状和废水流量的CFD分析结果。③1997年，Olson等人开发的热力学模型。这个模型以一个已完成的工业排水管道的气液两相研究成果为基础。

在2009年，在水环境研究基金会支持下，《排水系统通风研究报告》（以下简称《报告》）通过实测数据，对设计师广泛应用的以上三种模型做了比较和评价。《报告》认为没有一个模型与现场数据匹配得特别好，虽然经验推导模型倾向于高估排水管道内通风量，但是其计算结果是三个模型中最准确的，且使用起来非常方便。经验推导模型进行了相对小规模的实验，即在污水管道内用低流速诱导空气流动，缓慢移动的层流将在空气中产生最小的阻力并携带相对较小的空气，这种小规模实验在大型污水隧道中的应用具有一定的局限性。《报告》针对上述三个模型计算结果与实测数据做了对比，如图4-42所示。

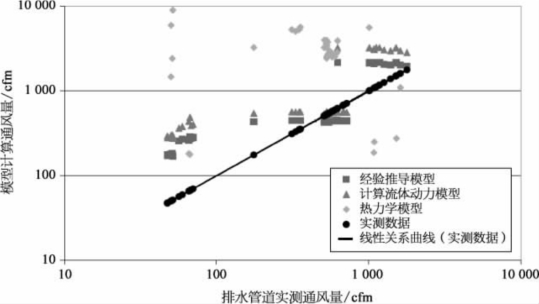
图4-42　不同排水管道空气动力学模型计算结果对比

（1）经验外推模型

Pescod和Price（1982）搭建了直径300mm 的实验室规模的重力管物理模型，测量各种水深、流速组合下的管道上部空间通风量。使用外推法，以300mm 管道的测量数据外推计算出重力流大管径的通风量，并应用于多个工程实践中。下式为Pescod和Price实验研究得到的重力流排水管道的通风-水力学能量关系式：(www.daowen.com)

式中 V——排水管道上部空间空气平均流速（m／s）；

　　 W——排水管道内水面宽度（m）；

　　 Vw——排水管道内水流平均速度（m／s）；

　　 Pair——排水管道干周，即管道断面周长减去湿周（m）。

根据《报告》实测通风量数据校核、验证，经验外推模型模拟结果与实测数据做比较，平均相对误差为103%，而且普遍比实测数据大，尤其在上下游通风受限的位置，误差最大。在每个测量点位置，经验模型模拟通风量数值变化不大。比如，在某些位置的实测通风量数值可能差4倍，但是经验模型模拟结果仅有5%的偏差。这是因为排水系统局部的水流流速变化比较小而导致的结果。

（2）计算流体动力学（CFD）模型

Edwini-Bonsu和Steffler（2004）开发了一个CFD模型，基于水面流速和水力几何学来估算排水管道上部通风量。对于层流和紊流两种气液条件，该CFD模型输出结果的适配关系式如下。

层流：

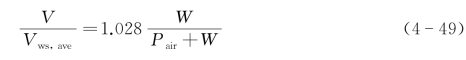
紊流：

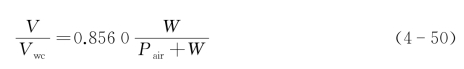
式中 Vws，ave——水流在气液交界面平均流速（m／s）；

　　 Vwc——水流在气液交界面中心线的流速（m／s）。

水流在水面中心线流速的计算，可以参考瓦诺尼法[Vanoni（1941）method]。该方法用来计算一条假设宽度无限的明渠在某个水深时的水流流速，如下式：

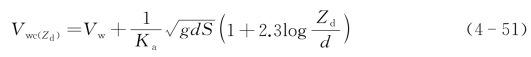
式中 ——明渠中心线处，距离渠底Zd处流速（m／s）；

　　 d——明渠中心线水深（m／s）；

　　 S——明渠坡度（m／s）；

　　 Kd——VonKarman常数，等于0.4。

等Zd等于d 时，中心线水面流速计算式如下：

参考Edwini-Bonsu和Steffler（2004）整合的关系式来计算水流的水面平均流速Vws，ave：

式中 y——距离水面中心线长度（m）。

这个CFD模型计算结果的准确度比经验外推模型更低，平均相对误差为173%，虽然计算结果与经验外推模型的计算结果在趋势上类似，但是在数值上更加过高估算通风量。这是因为，与经验外推模型一样，这个CFD模型也是基于管道几何结构和水流流速来预测管道上部通风量，并没有考虑其他干扰因素，比如温差引起的空气压力差、风速等。上述计算式会受到初始边界条件的限制，每根排水管道的边界条件都可能不同。为了得到更加准确的CFD模型模拟结果，需要对排水系统的每个独立组成部分分别建立、运行特定的模型。这样对于大多数工程项目来说，计算量将非常大。

（3）热力学模型

Olson等人（1997）为计算一个热动力系统的工艺输水管上部的空气流通而建立了一个数学模型，该输水管上部空间的空气，从输水管上游进入管道，从下游溢出管道。Olson模型有以下几个假设：①假设管道上下游各一个通风口，供空气进出；②调整对流热传递以适应埋地管道的实际情况；③工艺管道内的水自由流出管道系统，并假设为稳定流。

热力学模型如下式：

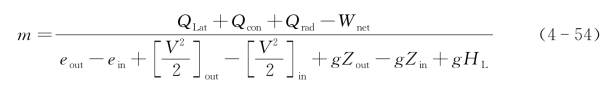
式中 m——空气流量（kg／s）；

　　 QLat、Qcon、Qrad——潜热传递、对流热传递和辐射热传递（J／s）；

　　 Wnet——气液界面间拖拽力、管道壁摩擦力对空气所做的功（J／s）；

　　 e——空气的比焓（J／kg）；

　　 Z——标高（m）；

　　 HL——空气流动过程中沿程水头损失（m）。

与《报告》实测通风量数据做比较，热力学模型计算结果的平均相对误差为3400%，很大程度是因为难以估算管道上部空气与土壤间的热传递。上式将各种机械能计算项（功、水头损失、动能、势能、重力流等）与热功相关的计算项（热传递、焓）混合到一起，意味着热工计算项将弱化机械能计算项；或者，如果热工计算项不显著，将导致计算结果出现渐进性偏差。