（1）深隧弗劳德数

在详细分析浪涌之前，可以通过深隧弗劳德系数的计算，对深隧是否产生显著浪涌现象进行初步评估：

式中 F——深隧弗劳德数；

　　 Q——峰值流量（m3／s）；

　　 g——重力加速度（m／s2）；

　　 D——深隧内径（m）。

根据Vasconcelos和Wright（2005）的计算，当深隧弗劳德系数小于0.3时，产生的浪涌有限。这个计算方法只是提供了一个初步的评判标准，因为深隧的系统配置影响因素较多，包括竖井的大小和形式、深隧的坡度、水流的分布、通风系统等，都可能产生浪涌。只有采用浪涌数学模型计算分析才可以充分论证是否会产生浪涌现象，上式计算得到的弗劳德数仅可作为初步参考。

（2）影响浪涌的关键要素

形成深隧浪涌的关键要素包括深隧内径、坡度、初始水位和进水流量，Karen E.Ridgway等人于2009年对影响深隧浪涌的各种因素做了尝试性研究。研究人员使用软件TAP（Transient Analysis Program），按照不同的管径、坡度、初始水位和进水流量建立了一系列数学模型，根据每个模型计算得到最高浪涌水位高度与管径、坡度、进水流量的对应关系，得出导致深隧浪涌进水流量拐点值的经验公式。

模型布局图如图4-35、图4-36所示。

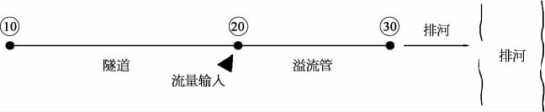
图4-35　浪涌研究TAP模型机理示意图

图4-36　研究模型纵断面示意图

随时间变化，水流从溢流竖井进入深隧，最高浪涌水位在水位抬升竖井内出现。进水流量在10s内由最小增加到最大，然后保持最大进水量直到模拟结束。溢流管非满流排入水体，管底标高可以决定深隧的初始水位，试验过程中，溢流管管底标高按照0.152m逐步降低，直到在水位抬升竖井内得到最高浪涌水位。同样，隧道内径、坡度也会做相应调整，以便得到不同内径、坡度的模拟结果。

研究结果表明，对于某一坡度、内径的深隧，有一个特定的进水量值。如果进水量大于这个数值，深隧会出现严重浪涌现象，这个特定进水量值称为拐点值。进水量拐点值与深隧内径呈线性关系，比如坡度为0.001的深隧，管径与进水流量拐点值的计算关系为：

式中 D——深隧管径（ft）；

　　 Q——进水流量拐点值（cfs）。

对于其他坡度的进水流量拐点值与管径的关系，参考图4-37。

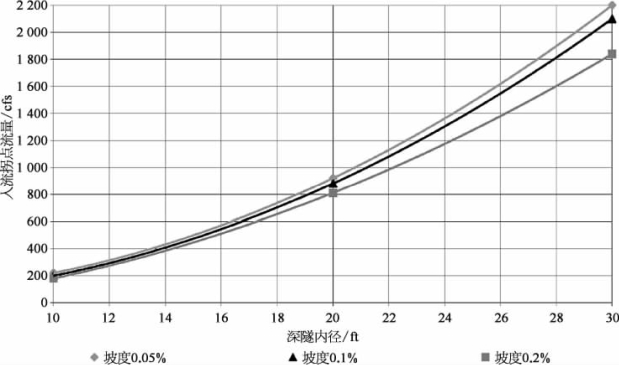
图4-37　深隧内径与入流拐点流量关系图

根据研究结果可知：①流量确定的情况下，隧道内径越小，越容易出现浪涌；②隧道坡度越大，越容易导致浪涌；③浪涌最高水位一般发生在深隧充满水的时候。同时，研究发现，隧道将要充满水时，浪涌导致的最高水位与深隧充满水时浪涌最高水位非常接近；④跌水竖井对浪涌有一定的缓冲能力，竖井内径越大，浪涌造成的水位波动幅度越小。

该研究成果仅仅采用了TAP软件的模拟结果，并未得到物理模型的验证，而且模型中隧道长度有限，对于大型深隧工程，该研究成果未必适用。但是，该研究可以让大家清楚地认识到深隧内径、坡度、进水流量、初始水位、竖井内径等对浪涌的影响，对深隧设计工作、水力模型专题研究工作等都具有指导性作用。

（3）浪涌分析数学模型

导致浪涌现象的因素很多，产生机理复杂。对浪涌现象做相对准确的分析，需要引入计算机数学模型技术。数学模型分析浪涌现象遇到的难题有三个：①浪涌现象为瞬时水压波动，数学模型需要有处理管道局部极短的时间步长的能力，使得计算更准确，同时使模型运行时间最小化；②气爆导致浪涌的出现与空气传输有关，如何处理气—液两相流也是目前浪涌分析软件仍未解决的问题；③明渠流与压力流流态不同，计算机理也不同，如何处理两种流态交接点的水力学计算，同样也是浪涌分析软件必须面对的问题。

美国在深隧浪涌分析研究方面处于世界领先水平，并经过了大量工程实践应用，包括浪涌分析数学模型研究和开发，比如应用科学有限公司（Applied Science，Inc）开发的数学模型软件TAP，在多个深隧工程项目中得到应用，包括深圳前海深隧项目。实践证明，该软件可以相对准确地分析深隧系统的浪涌现象，并得到多位深隧专家的认可。当然，其他一些软件在深隧项目中也有应用，比如ITM（Illinois Transient Model）、MXTRANS等。其中，ITM 软件是芝加哥TARP项目数学模型专题研究成果之一。

可以应用于深隧浪涌分析的典型计算机软件，通常会对传统流体动力学算法做改进并引入几个关键数学模型，从而解决以上三个问题。本文简单介绍TAP软件解决这些问题的方法和对策，对深隧浪涌分析工作中如何选择数学模型软件以及应用有方向性指导。

（4）求解圣维南方程

通常来说，对菱柱形明渠的非稳态模拟以圣维南方程组为基础，其由连续方程和运动方程组成[式（4-36）和式（4-37）]。方程假设流体不可压缩，不考虑水流沿长度方向的横向交换。

式中 A——断面面积；

　　 Q——流量；

　　 g——重力加速度；

　　 I——从自由液面至计算断面的惯性矩；

　　 S0——管段坡度；

　　 Sf——水力坡度。

由于式（4-36）和式（4-37）是一阶拟双曲型偏微分方程组，无法使用差分法来模拟测压管水头线的不连续性。举例来说，当使用特征线法（MOC），空间导数（∂／∂x）在x方向上非连续点无法求解。此外，另一个问题是明渠流动和满管流之间的转变需要特殊处理。因为圣维南方程不能直接应用于满管流（有压）条件，需要修正。

如下所述，针对这种明渠流动和满管流之间的转变过程中的测压管水头线的不连续问题，通常使用的计算方法有两种。其一为交界面跟踪程序（interface tracking programs），如MXTRANS软件；其二为震动追踪程序（shock-capturing programs），如TAP软件使用有限体积法。

两种类型的计算程序都做出了一些一般的假设，以避免出现空的干管。此外，大多数计算程序允许空气在从明渠流动和满管流之间的转变过程中能与大气完成充分的气体交换（后文简称“完美通风”）。(www.daowen.com)

（5）交界面追踪程序

交界面跟踪程序是在20世纪70年代和80年代开发的，应用特征线法模拟从明渠流动和满管流转变过程中的波阵面（wavefronts），并通过震动配符程序（shockfitting programs）追踪增压或减压波阵面在渠道或管道中的移动过程。

（6）震动追踪程序

震动追踪程序借助其非线性数值求解方法和有限体积法，应用愈发广泛。作为震动追踪程序的一种，TAP使用有限体积法来求解非线性圣维南方程组。对于每个时间步长，在每个网格单元计算网格中心点求解A 和Q。这些变量的更新取决于跨越单元格边界的通量的计算，使用近似黎曼求解器（Riemann solvers）计算。

冲击追踪程序通常使用Preissmann窄槽技术处理不同流态之间的转换。Preissmann窄槽概念允许将单个方程组同时应用于明渠和有压流的模拟计算中。

使用管道内有压流部分的水流速度来对应估算有气体部分的气体声波速度，再以此估算槽段的宽度。计算槽宽度以匹配导管系统的加压部分中的水的估计声波速度。对于每秒121.8～1218m 的声波速度，槽中部分可忽略不计。

Preissmann窄槽宽度以下列方式计算。

式中 Bslot——槽宽；

　　 Afull——管段横断面面积；

　　 g——重力加速度；

　　 a——声波速度。

Preissmann窄槽概念的一个缺点是，由于在整个管道系统中施加了完美通风，导致其无法描述满管的、流体压力低于大气压的流动状况。而TAP克服了该缺点。对某一网格单元，当相邻网格或网格连接面处的压力值为大气压强时，则该网格的流动状态恢复至明渠流态。当流体压力低于大气压，TAP假设槽宽（Bslot）延伸至管道顶部。通过在TAP中进行设定，空气可通过该槽进入计算域。

（7）罗伊一阶迎风格式（Roe's first order upwind scheme）

在TAP中，导管被分成小的、等间隔的网格单元，通过罗伊一阶迎风格式得到等距排布网格中心点的A和Q值。依据Jacobian矩阵局部线性排布，Riemann求解器求得每个时间步长的网格单元交界面处的通过流量通量。该值仅取决于相邻网格单元的求解条件，并且其线性排布应满足Rankine- Hugoniot假设，同时满足该处的函数不连续性。

其后，使用式（4-39）在网格单元i处更新速度矢量U=[A，Q]T：

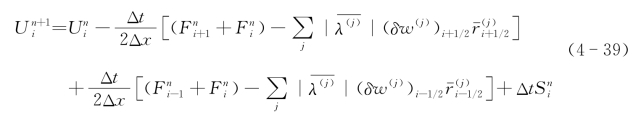
式中 n——时间步长指数；

　　 λ（j）——近似特征值，对应的特征向量为r（j），它的值首先需要计算网格单元连接面（i，i+1）处的Roe平均值。

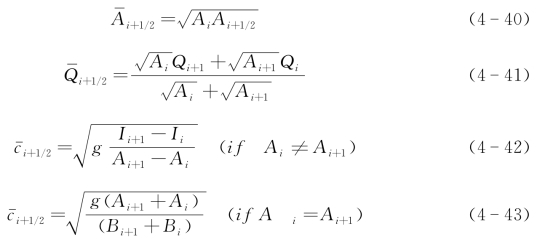
式中 B——网格单元中自由液面的顶宽。第一动量惯量Ii的值由Ii=Aihc，i 确定，其中，hc，i是流动横截面积的自由表面和质心之间的距离。通过计算Roe平均值，可以获得连接面（i，i+1）上的近似特征值λ（1），（2）和特征向量r（1），（2）。

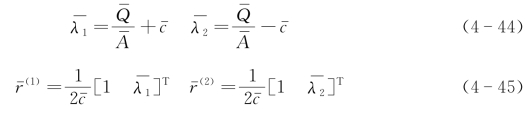
最后，穿过该网格单元的波强使用相界面处的变量δw 表示，其可通过式（4-46）计算得到。

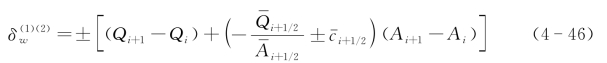
由于此数值离散求解方法为显式，该系统必须满足库朗法则。因此，需要在每个时间步长（dT）嵌入以下最大值限定：

式中 dX——计算网格单元长度；

　　 Cr——库朗常数，通常取0.9。

使用Roe一阶迎风差分格式时，由于明渠至满管区段内相界面处压力的升高，引起数值振荡。这些振荡可能相对较小，忽略声波速度的条件下，其值为每秒121.8m。

（8）局部时间步长（Local Time Stepping）

等TAP使用小的时间步长对每个小单元格进行详细计算时，模型运行时间成为关注点。可使用TAP内局部时间步进（Local Time Stepping）程序来保持数值稳定性，同时最小化模型运行时间。相对于整个系统调整时间步长，局部时间步进程序所需的总计算量会显著减少。

稳定计算的时间步长与式（4-47）给出的库朗法则有关。库朗法则指出，时间步长必须小于单元长度除以波速加上单元格中平均速度绝对值的总和。在明渠流动条件下，波速通常小于3.05m／s，但是在满管（加压）条件下，波速成为声波速度。对于管道内的水，声波速度通常为每秒121.8～1218m。这意味着，根据流量状态，模型中所需的时间步长可以在系统中的通道／导管之间变化1～2个数量级。

对于每个单元，计算波速和加速度的绝对值之和。对于每段管段，对这些最大值作加和，并用来计算满足库朗法则的前提下的最大时间步长，其中，Cr=0.9。

模型的时间步长被选择为管段最小允许时间步长。对于具有小于或等于模型时间步长的两倍的允许时间步长的管道，使用模型时间步长对这些管道进行计算。

模型时间步长不允许变化太快，否则会引起不稳定状态。在每个时间步长间，变化幅度不得大于10%。

模型每计算一次，时间步长的个数的设置不得小于25个。这为整个系统提供了一系列的条件，使模拟过程中出现不稳定中间结果时，模型可以反复迭代计算，用来保证系统稳定性。

综上所述，适合用来做深隧浪涌分析的软件，需要具备的功能包括：①处理明渠流和压力流交界面水力计算的能力；②自动调整局部管道运行时间步长的能力，并且能够模拟管道水压的瞬态变化过程；③至少在一定程度上可以模拟计算局部出现负压时系统压力变化的能力。目前，多个排水系统模拟软件在国内水务设计领域得到应用，但并不是所有软件都具备分析深隧浪涌现象的能力，比如Info Works、MIKE Urban、SWWM、Water Hammer等。不同软件对浪涌现象的模拟结果对比，本书不作细述。

深隧按照其使用功能有不同的类型，有些类型的深隧，由于流量相对稳定或进水量比较小，一般不会发生严重的浪涌现象，比如污水转输深隧、初雨调蓄深隧，在保障完善的通风系统的条件下，可以不必做浪涌分析。对于排涝深隧和复合型深隧，进水量变化大、峰值条件下流速大，更容易出现严重的浪涌现象，为了保障深隧将来的运行安全，必须做详细的浪涌分析，确保设计方案的安全性。

目前，国内对于深隧内水动力瞬态模型软件的研发和应用，还没有出现积极的成果。需要注意的是，美国开发出的数学模型仍具有诸多限制因素：①对于空气在深隧系统的传输，尤其是气穴引起的增压现象，数学模型无法模拟，一般都假设明渠流到有压流过渡过程中，气体可以完全排放；②当压力低于气化压强时，模型无法处理气化现象，仅可以处理压力低至气化压强时管道内压力情况；③对于大型深隧工程，数学模型计算结果对输入数据过于敏感；④模型模拟所涉及的改善措施需要与实际工程解决方案相结合。数学模型模拟始终与工程实际有出入。

空气传输会导致深隧数学模型建模、运行非常复杂，考虑到深隧两相动力流中水动力占主导地位，因此，目前广泛应用于深隧设计的数学模型往往会弱化空气动力学因素对浪涌现象的影响。实际设计工作中，对气相因素的处理办法为：①不明确模拟空气传输，但是数学模型需要输入大气边界条件，模拟结果可以预测高压空腔可能出现的位置和体积；②模型可以模拟出负压“空包”位置，在该“空包”消失后会导致类似水锤现象的瞬时水压波动。