2.1.2.1　城市化对地表径流的影响

与城市发展前的自然地表相比，城市不透水地面面积增加，排水管道覆盖率不断加大，排水速度也随之加快，使得雨水向排水管网中的输送更为迅速、汇流时间缩短，最终导致洪水流量增加，暴雨造成的危害也会加剧。在暴雨径流过程中，表现为流量过程曲线急升降、峰值增大、峰值出现时间提前，雨停之后，补给退水过程的水量少，整个洪水过程线底宽变窄，客观上增加了洪涝灾害发生的概率。城市发展引起的径流过程线的变化趋势，如图2-2、图2-3所示。

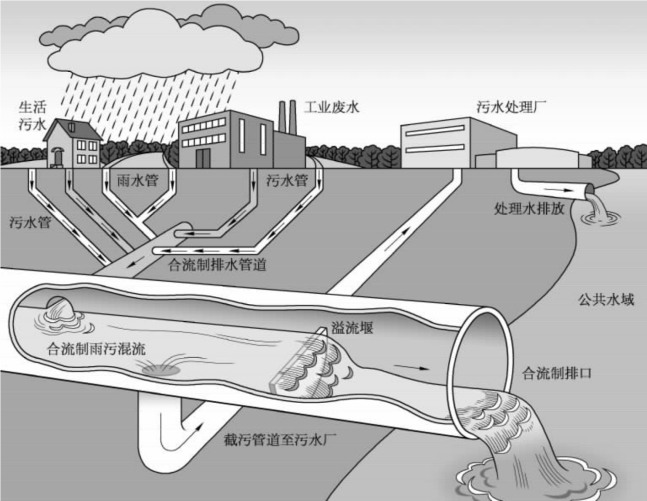
图2-1　城市河道面源污染产生过程示意图

2.1.2.2　城市径流量计算

深隧规模设计与暴雨强度、城市下垫面、浅层排水系统整体排水能力以及城市防涝标准有关系，涉及的数据量非常庞大，使用传统的排水管道设计方法来准确论证深隧设计规模，几乎是难以做到的事情，尤其对于计算城市内涝水深、退水时间等。因此，我们引进了排水系统专业软件，利用强大的计算机技术，输入城市下垫面、排水系统、降雨曲线等详细信息，综合论证深隧设计规模。

计算降雨-产流的方法很多，有经验公式，也有概念模型。目前，多款专业软件得到广泛应用，比如美国环保局的SWMM、DHI公司推出的MIKE Urban及原WallingFord公司推出的InfoWorksICM 等专业计算机模拟软件，用来模拟计算城市复杂的地表径流产流过程。每种软件都内置多种径流计算模型，每个径流模型在分析和计算暴雨径流方面都有自己的长处和局限性。合理选择径流模型来计算暴雨造成的径流强度，对提高城市雨水系统设计的科学性，优化城市排水、雨洪污染控制以及水资源利用，增强城市的防洪抗灾能力都具有重要意义。

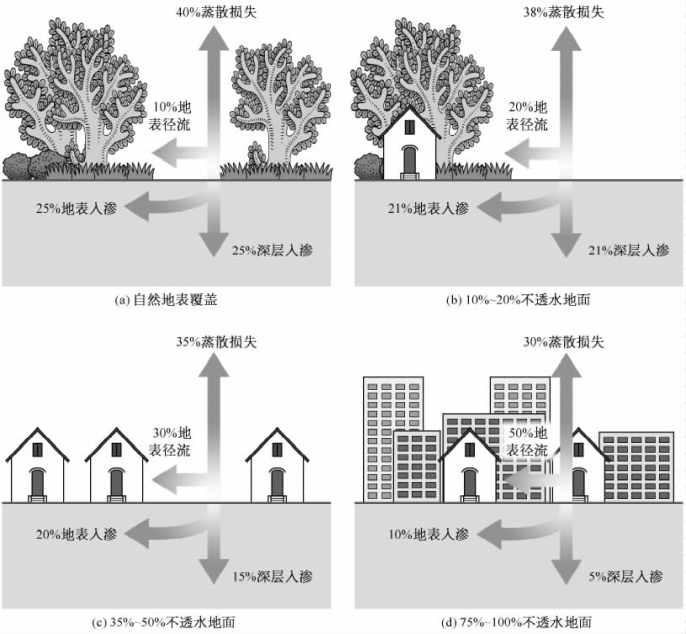
图2-2　不透水地面覆盖率与地表径流的关系

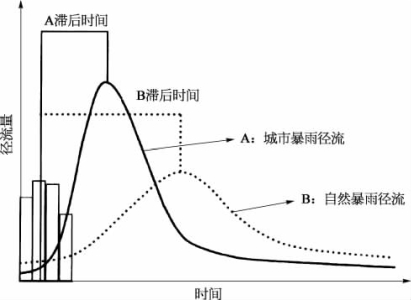
图2-3　城市发展引起的地表径流变化

我国幅员辽阔，东、西部城市水文地质条件差异明显，不可能采用统一的径流模型来模拟计算所有城市的径流过程。径流模型和各种模拟参数的选择，必须经过本地降雨、管道流量实测数据的严格校核，确保计算机模型符合当地实际水文特征，尤其对于地表产流受土壤先期含水率影响比较大的渗透地面，比如郊区、公园绿地、林地、山地等。本节介绍几种Info Works ICM 软件应用到的降雨-产流计算方法，让读者对计算机模拟软件的径流计算过程有所了解，并可以此类推到其他模拟软件的径流计算过程，进一步应用于城市排水系统规划、设计等实际工作中。

传统雨水管道设计中，径流过程线所表达的径流量-时间关系曲线，是由随径流时间而变化的暴雨强度公式来表达。区别于传统计算方法，计算机模拟软件所有应用到的径流模型都包含两个模型：径流量计算模型和径流过程分配模型。由此，可以仿真模拟计算真实降雨过程的产流过程，继而使用2D技术准确计算城市内涝分布和退水时间。

（1）径流系数模型法

径流系数模型法一般用来模拟城市密集建成区的非渗透地面或地表径流过程受土壤先行条件影响比较小的可渗透地面。对于受土壤先行条件影响比较大的汇水区域，建议使用其他径流模型，比如美国国家土壤保护局（Soil Conservation Service，SCS）径流模型。

降落到地面的雨水，一部分被植物和地面洼地截流，一部分渗入土壤成为地下水的一部分，其余部分雨水在地表产生径流，这部分雨水量称为径流量。

式中 R——径流深度（mm）；

　　 P——降雨深度（mm）；

　　 ψ——径流系数，径流量与降雨量的比值。

径流系数是一个统计性系数，用来计算一个区域在较长时间内的平均径流量。当一个区域内包含多种土地利用类型时，区域的径流系数由各种土地利用类型加权平均得到综合径流系数。参考《室外排水设计规范》（GB50014—2006）（2016版），各种下垫面的径流系数按表2-1取值。典型城市区域综合径流系数按表2-2取值。

表2-1　城市地表径流系数

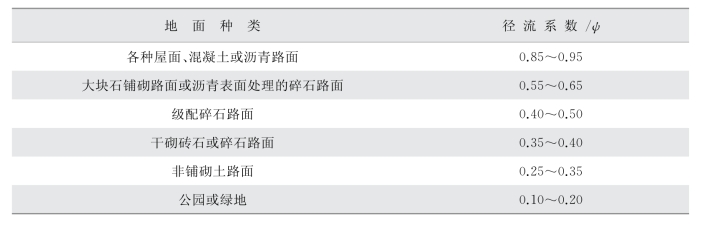
表2-2　综合径流系数

计算机软件内置的径流量模型使用降雨深度、汇水区域面积、径流系数等数值，可以计算出某个汇水区域在一定降雨深度情况下产生的径流量。对于计算出的径流量如何在时间上分配，则需要引进径流过程分配模型（Runoff Routing Model）。对于城市径流模型，Info Works ICM 内置了多种径流过程分配模型，其中双线性水塘模型（Double Linear Reservoir，DLR）用来模拟每个汇水面积内产流的时间分配，其蓄水-输出关系如图2-4所示。

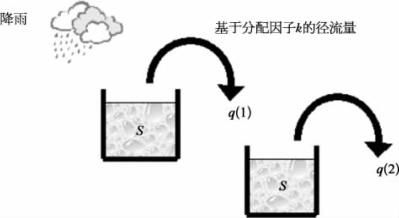
图2-4　双线性水塘蓄水-输出关系示意图

DLR模型涉及连续两次蓄水-输出量计算，S 用来模拟现实径流产生过程中的降雨量初损，计算出的q（2）进入排水管网。每个水塘的蓄水-输出关系如下：

式中 k——分配因子系数；

　　 q——输出流量。

式中 I*=0.5（1+I10），I10 为10min平均降雨深度。

式中 s——汇水区域内地面坡度；

　　 A——汇水区域面积（m2）。

Sarginson和Nussey第一次在英国使用了这种形式的径流分配模型，其中C 的取值经过了优化推算，式（2-2）的计算关系是经过在英国数十个小汇水区域实测流量数据的严格校核的结果。

DLR模型在运用的时候，需要注意Info Works ICM 有几点限制条件和假设：如果地面坡度s＜0.002，则s的取值为0.002；如果汇水区域面积A＜1000，则计算C 值的时候取值1000；如果汇水区域面积A＞10000，则计算C 值的时候取值10000。DLR径流分配模型仅适用于面积小于1hm2 的汇水区域，如果汇水区域面积大于1hm2，InfoWorks ICM 建议使用另外一个径流分配模型：大型汇水区域模型（Large Contributing Area Model，LCAM）。

LCAM 模型的计算模式与DLR模型相同，也是双线性水塘模型。为了更加准确地计算大汇水区域的峰值径流的滞后时间和峰值衰减量，引入了两个修正参数：分配因子乘数、滞后时间。LCAM 模型的分配因子乘数计算与DLR不同。

式中 A——汇水区域面积（m2）；

　　 s——汇水区域地面坡度，最小值不小于0.002；

　　 L——汇水区域最远点到集水口间的长度（m）。

其他等式参数取值为：Ck=0.03，k1=-0.022，k2=-0.228，k3=0.46。

峰值滞后时间计算如下：

式中等式参数取值为：Ct=4.334，t1=0.009，t2=-0.173，t3=0.462。

无论使用任何一款模拟软件、选择任何一个径流模型，使用者必须先弄清径流模型的工作原理和适用范围，比如DLR和LCAM 径流分配模型，其产生的依据为英国当地多个汇水区域的实测数据，是否适用于当地的排水工程项目，必须采用当地实测数据对模型进行校核和验证，必要的时候，模拟参数做调整。

（2）SCS径流模型法

径流系数模型法适用于非渗透地表或受土壤先期饱和率（Antecedent Moisture Conditions，AMC）影响比较小的渗透地表的产流计算，对于大面积公园绿地、郊区、山地等受土壤先期饱和率影响比较大的可渗透汇水区域，建议使用SCS或其他适合的径流模型。(www.daowen.com)

SCS径流模型发源于美国国家土壤保护局的径流计算模型，并经过了半个世纪的发展和修订。目前，该模型在美国、法国、德国、澳大利亚和非洲部分国家得到广泛应用。SCS径流模型详细资料可以参考美国SCS工程师手册第4部分。本章仅对其主要参数做简单介绍。

可渗透汇水区域的径流过程受土壤先期饱和率影响比较大，具体体现为径流量的衰减和径流峰值的滞后。对于一场特定降雨，如果前5天有过降雨，该场降雨前的土壤含水率比较饱和，则将产生比较大的径流。该模型为了模拟径流量的衰减和径流峰值的滞后，引入了三个基本概念：

①滞洪深度：极端降雨事件下，整个持续降雨过程中降雨量的损失量。

②汇水区域土壤饱和率指数：在土壤干燥或湿润情况下，用来修正蓄水深度。

③初始损失因数：用来确定降雨的初期损失量。

如表2-3所示汇水区域饱和率指数1、2、3分别代表三种土壤湿润状态：干燥、中度和潮湿。在模型中，与滞洪深度有关的计算数据（CN值）按照中度土壤湿润状态为准作为计算依据，然后按照饱和率指数做相应调整。

表2-3　蓄水深度调整系数表

①滞洪深度计算公式：

式中 S——滞洪深度（m）；

　　 CN——径流曲线数。

CN值是一个与径流量有关系的多个因素的综合径流因子，包括土壤类型、土地使用类型、植被覆盖、城市化程度以及土壤先期饱和率等。CN 值的取值为0～100，代表一个汇流区域的地表径流产流潜力，数值越高，产流潜力越大，0代表着没有径流的产生，100代表降雨量全部产生径流，与径流系数比较类似。

CN值的确定需要两部分地理信息：土地规划信息和土壤类型分布信息。径流曲线数CN值的取值，美国农业局建议数值见表2-4。农业局原建议CN值列表中包含各种农田、耕地、果园、森林、牧场、树林、城市等不同植被覆盖地表，在不同土壤类型和径流潜力条件下的CN值，这里不做赘述，仅列出与城市排水系统设计有关系的地表CN值，供参考。如果对其他地表CN值有兴趣，可以查阅相关资料。

表2-4　径流曲线表

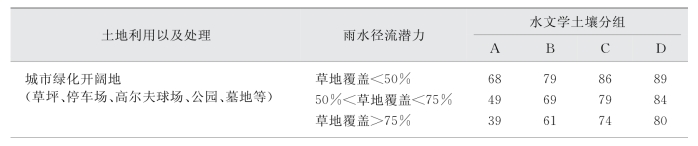
（续表）

②初期损失量计算公式：

式中 S——滞洪深度（m）；

　　 k——初期损失因数，0＜k≤0.2。

原SCS模型推荐k=0.2，后续的一些研究认为k=0.05～0.1更恰当，Info Works ICM 软件默认取k=0.1。当然，该软件允许用户直接定义某个汇水区域的Ia值，以此取代默认k 值计算出的Ia值，使模型更符合用户的要求。

③SCS径流模型计算径流量的基础为连续性方程：

式中 P——总降雨深度（mm）；

　　 Ia——初期损失（mm）；

　　 F——累积滞留损失（mm）；

　　 Q——径流深度（mm）。

降雨量、滞留量、径流量之间的关系：

由式（2-9）和（2-10）可以推导出SCS径流量计算公式：

④SCS单位过程线模型。明确SCS径流模型后，就需要将计算得到的径流量进行径流过程分配。SCS径流模型采用无量纲单位过程线模型进行径流量过程分配。

以大量汇水区域（美国境内）降雨、流量实测数据为依据，推导得出一个无量纲单位过程曲线，为无量纲时间（t／tp）-流量（q／qp）数值关系曲线（其中tp为径流峰值出现时间，qp为径流峰值），即为SCS单位过程曲线，如图2-5所示。

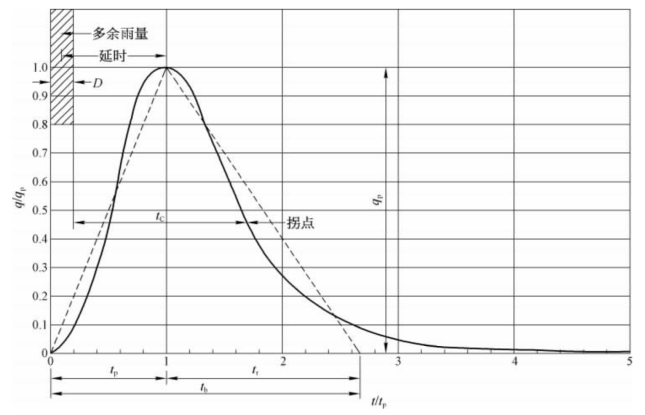
图2-5　SCS无量纲单位过程曲线

径流量分配计算过程中，涉及两个参数的计算：峰值时间tp和径流峰值qp。在使用单位过程曲线法时，峰值时间tp和径流分配过程总时间长度tb为：

式中 tc——汇水区域集水时间，即汇水区域最远点到管网收水点的流经时间（s）。

集水时间与地表性质、坡度、面积大小、径流长度等因素有关。目前，存在多种集水时间的计算方法，在此，仅介绍SCS针对郊区汇水区域集水时间的计算公式：

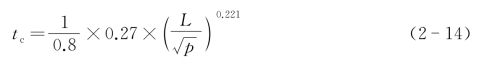
式中 L——汇水区域径流长度，即最远点到管网收水点长度（km）；

　　 p——汇水区域地面坡度（mm）。

径流峰值计算：

式中 A——汇水区域面积（km2）；

　　 Q——汇水区域径流深度（mm），见式（2-11）；

　　 tp——峰值时间（h）。

综上所述，可知：SCS径流模型包括SCS径流深度计算模型和SCS单位过程线模型；SCS径流模型推导依据为美国境内数十个汇水区域降雨、流量实测数据，是否适用于项目目标城市，采用的各个模拟参数、水力参数必须经过当地实测数据严格校核；按照式（2-11）计算径流深度；按照式（2-12）计算径流峰值时间；按照式（2-15）计算径流峰值。

工程师在实际设计工作中，可以将实际降雨曲线或设计降雨曲线按时间步长分段，比如时间步长5min。分别计算每个时间段降雨产生的径流深度、峰值时间、径流峰值，按照单位过程线分配径流量形成径流曲线，最后将每个时间段径流曲线叠加，形成整个降雨过程的径流曲线。