对于交通分配，国内外进行过较多的研究，数学规划方法、图论方法及计算机技术的发展，为合理的交通分配模型的研制及应用提供了坚实的基础。国际上通常将交通分配方法分为平衡模型和非平衡模型两大类，并以Wardrop第一、第二原理为划分依据。

非平衡模型具有结果简单、概念明确、计算简便等优点，因此在实际工程中得到了广泛应用。非平衡模型根据其分配手段可分为无迭代和有迭代两类，就其分配形态可分为单路径和多路径两类。非平衡模型分类如表7-16所示。

表7-16　非平衡模型分类

1. 最短路交通分配方法

最短路交通分配是一种静态的交通分配方法。在该分配方法中，取路权为常数，即假设车辆的平均行驶车速不受交通负荷的影响。每一OD点对的OD量被全部分配在连接该OD点对的最短线路上，其他道路上分配不到交通量。

这种分配方法的优点是计算相当简便，其致命缺点是出行量分布不均匀，出行量全部集中在最短路上。这种分配方法是其他各种交通分配方法的基础。

由于在最短分配过程中，每一OD点对的OD量被全部分配在连接该OD点对的最短路线上，因此通常采用最短路分配方法确定道路交通的主流向。

图7-5所示为最短路分配方法流程图。

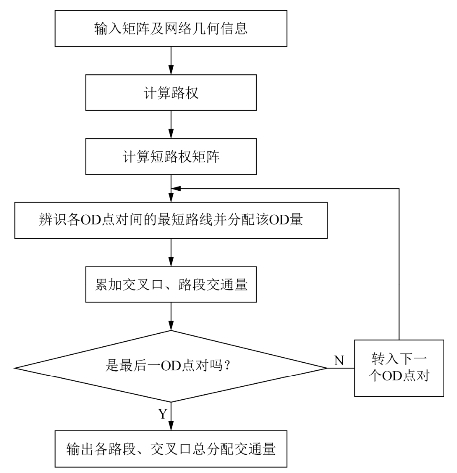
图7-5　最短路分配方法流程图

【例7-6】在图7-6所示的交通网络中，交通节点1、3、7、9分别为A、B、C、D四个交通区的作用点，四个交通区的出行OD矩阵如表7-17所示。试用最短路法分配该OD矩阵。

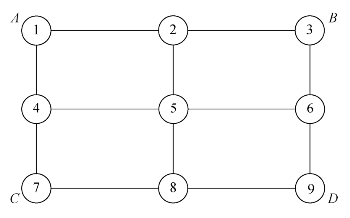
图7-6　交通分配网络

表7-17　OD矩阵　（单位为辆/h）

【解】（1）确定路段行驶时间。用最短路法分配交通量时，首先要确定路段行驶时间t(i,j)，在该法中取t(i,j)为常数。对于现状网络的交通分配，可根据现状网络的实测路段车速与路段长度确定；对于规划网络的交通分配，可根据路段设计车速确定行驶时间。在本例中确定的路段行驶时间t(i,j) 如图7-7所示。

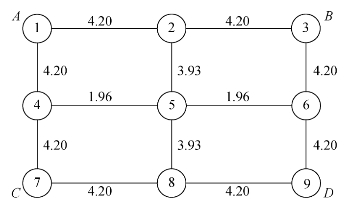
图7-7　路段行驶时间（单位为min）

（2）确定最短路线。各OD量作用点间的最短路线可用寻找最短路的各种方法确定，详见《道路交通工程系统分析方法》（王炜等，人民交通出版社，2004年）。在本例中，最短路线如表7-18所示。

表7-18　最短路线

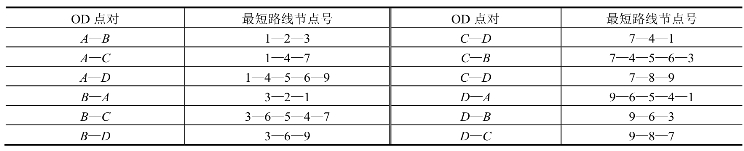
（3）分配OD量。将各OD点对的OD量分配到该OD点对相对应的最短路线上，并进行累加，得到图7-8所示的分配结果。

2. 容量限制交通分配方法(www.daowen.com)

容量限制交通分配是一种动态交通分配方法，它考虑了路权与交通负荷之间的关系，即考虑了道路通行能力的限制，比较符合实际情况，该方法在国际上比较通用。

采用容量限制分配模型分配出行量时，需先将OD表中的每一OD量分解成K部分，即将原OD表（n×n阶，n为出行发生、吸引点个数）分解成K个OD分表（n×n阶），然后分K次用最短路分配模型分配OD量，每次分配一个OD分表，并且每分配一次，路权修正一次，路权采用路阻函数修正，直到把K个OD分表全部分配在网络上。容量限制交通分配方法流程图如图7-9所示。

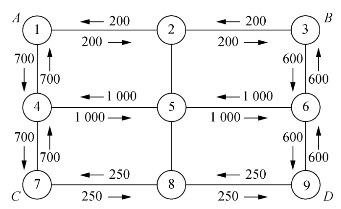
图7-8　分配交通量（单位为辆/h）

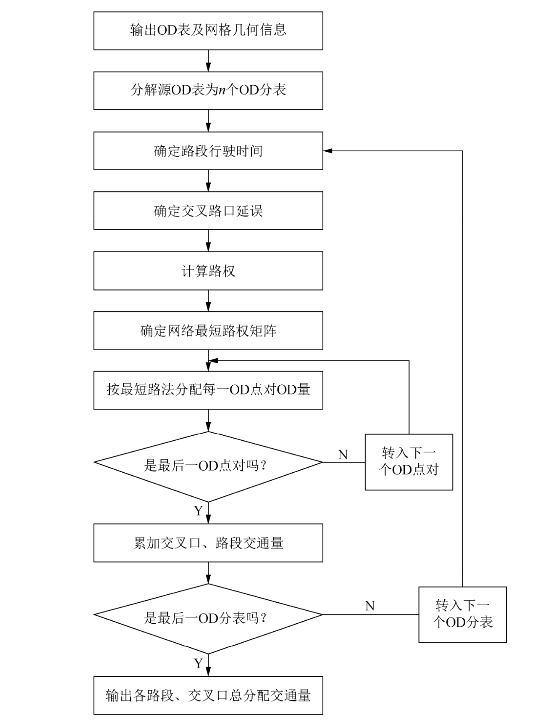
图7-9　容量限制交通分配方法流程图

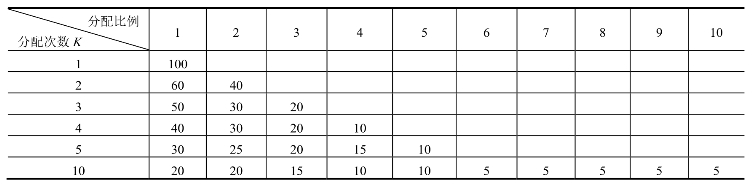
在具体应用时，视道路网络的大小，根据表7-19选取分配次数K及每次分配的OD量比例。

表7-19　分配次数K及每次分配的OD量分配率

【例7-7】 用容量限制分配方法求解例7-6所示的交通分配问题。其中，设主干线4——5——6，2——5——8的单向自行车交通量均为3 000辆/h，其他路段的单向自行车交通量均为2 000辆/h。

【解】本例采用五级分配制，第一次分配OD量的30%，第二次分配25%，第三次分配20%，第四次分配15%，第五次分配10%。

每次分配采用最短路分配模型，每分配一次，路权修正一次，采用美国联邦公路局路阻函数模型对路权进行修正。分配交通量如图7-10所示。

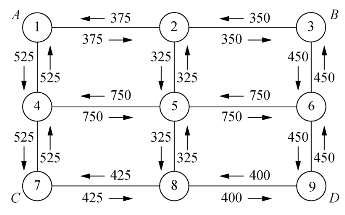
图7-10　分配交通量（单位辆/h）

3. 多路径交通分配方法

由出行者的路径选择特性可知，出行者总是希望选择最合适（最短、最快、最方便等）的路线出行，称为最短路因素。由于交通网络的复杂性及交通状况的随机性，出行者在选择出行路线时往往带有不确定性，称为随机因素。这两种因素存在于出行者的整个出行过程中，两种因素所处的主次地位取决于可供选择的出行路线的路权差（行驶时间差或费用差等）。因此，各出行路线被选用的概率可采用Logit型的路径选择模型计算，即

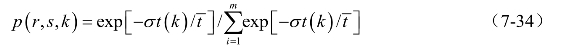
式中：p(r,s,k)——OD量T(r,s)在第k条出行路线上的分配率；

t(k)——第k条出行路线的路权（行驶时间）；

——各出行路线的平均路权（行驶时间）；

σ——分配参数；

m——有效出行路线条数。

本分配模型能较好地反映路径选择过程中的最短路因素及随机因素。实际上，若出行路线路权相同，则本模型称为随机分配模型，各路线被选用的概率相同。若某一路线的路权远远小于其他路线，则本模型称为最短路分配模型，它是一种改进型的多路径分配模型。改进的多路径分配模型虽然与Dial模型在形式上很类似，但新模型具有新含义与内容，特别是在参数σ的确定、路径的选取及算法上与Dial模型有本质的区别。