交通分布预测是交通规划四阶段预测模型的第二步，是指把交通的发生与吸引量预测获得的各小区的出行量转换为各小区之间的空间OD量，即OD矩阵。

图7-3所示为交通小区i和交通小区j之间的交通分布的示意图。Qij表示交通小区i到交通小区j的交通量，即分布交通量。同样，Qji表示由交通小区j到交通小区i的交通量。

图7-3　交通分布示意图

交通分布预测主要有增长系数法和重力模型法。

1. 增长系数法

在交通分布预测中，增长系数法的原理是假定在现状交通分布量给定的情况下，预测将来的交通分布量。

根据函数的种类不同，增长系数法可以分为常增长系数法（Unique Growth Factor Method）、平均增长系数法（Average Growth Factor Method）、底特律法（Detroit Method）和福莱特法（Fratar Method）等，下面分别讲述。

1）常增长系数法（Unique Growth Factor Method）

常增长系数法假定qij增长仅与i小区的发生量的增长率有关，或仅与j小区的吸引量增长率有关，或仅与生成量的增长率有关，是一个常量。

增长函数为

该方法只考虑将来的发生量或吸引量或生成量当中的某一个量的增长率对函数的影响，忽略其他变量对增长函数的影响。由于产生量与吸引量的不对称性，因此其预测精度不高，不需要迭代计算，是一种最简单的方法，但其有时不能保证交通分布的守恒约束条件。

【例7-4】 试利用例7-2中三个小区目标发生交通量预测值和基础年的出行分布矩阵（表7-5），求解目标年的出行分布矩阵。

表7-5　现状OD表和将来各小区的预测值　（单位：万次）

【解】（1）求各小区的发生增长系数：

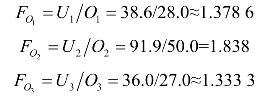
（2）以表7-5为基础矩阵，各项均乘以发生增长系数，得到表7-6。

表7-6　常增长系数法计算得到的OD表　（单位：万次）

此OD表满足出行发生的约束条件，故为所求的将来年分布矩阵。

2）平均增长系数法（Average Growth Factor Method）

平均增长系数法假定i，j小区之间的交通分布量qij的增长系数是小区i出行发生量增长系数和小区j出行吸引量增长系数的平均值，即

3）底特律法（Detroit Method）

底特律法假设，小区间交通分布量qij增长系数与小区i出行发生量和小区j出行吸引量增长系数之积成正比，与全规划区出行生成总量的增长系数成反比，即

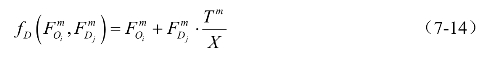
4）福莱特法（Fratar Method）

福莱特法假设i小区间分布交通量qij增长系数不仅与i小区的发生增长系数和j小区的吸引增长系数有关，还与整个规划区域的其他交通小区的增长系数有关。

模型公式为

式中：Li——i小区的位置系数；

Lj——j小区的位置系数。

2. 重力模型法

重力模型法是一种常用的方法，它根据牛顿的万有引力定律，即两个物体之间的引力与两个物体的质量之积成正比，而与它们之间距离的平方成反比类推而成。

重力模型法预测出行分布考虑了两个交通小区的吸引强度和它们之间的阻力，认为两个交通小区出行吸引与两个交通小区的出行发生量成正比，而与交通小区之间的交通阻抗成反比。在用重力模型进行出行分布预测时，可采用以下几种模型。

1）无约束重力模型

Casey在1995年提出如下重力模型，该模型又称最早出现的重力模型，即

式中：pi，pj——分别表示i小区和j小区的人口；

dij——i，j小区之间的距离；

α——系数。

此模型为无约束重力模型，模型本身不满足交通守恒约束条件中的任何一个，即

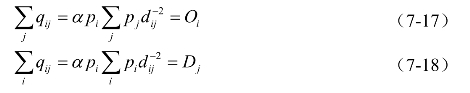
该模型简单地模仿牛顿的万有引力定律，后来人们对其进行改进，包括出行总数代替总人口数，将dij的幂扩展为参数γ（其值一般为0.6～3.5）。一般可以用出行费用函数f (cij)来表示，因此，重力模型可表示为

常见的交通阻抗函数有以下几种形式。

幂函数：

指数函数：

组合函数：

式中，κ，γ——参数。

待定系数κ、γ根据现状OD调查资料，利用最小二乘法确定。此时可将模型取对数，使之线性化来求得。

【例7-5】 现状OD表和将来各小区的预测值如表7-7所示，将来的发生与吸引交通量如表7-8所示，现状和将来行驶时间如表7-9和表7-10所示，试利用重力模型和平均增长系数法，求出将来OD表。设定收敛标准为ε=1%。

表7-7　现状OD表和将来各小区的预测值　（单位：万次）

表7-8　将来的发生与吸引交通量

表7-9　现状行驶时间

(www.daowen.com)

表7-10　将来行驶时间

【解】（1）用下面的无约束重力模型：

两边取对数，得

式中：qij，OiDj，cij——已知常数；

α，β，γ——待标定参数。

令y=ln(qij)，a0=lnα，a1=β，a2=-γ，x1=ln(OiDj)，x2=ln(cij)，则式（7-24）转换为

此方程为二元线性回归方程，a0，a1，a2为待标定系数，通过表7-7和表7-9获取九个样本数据，如表7-11所示。

表7-11　样本数据

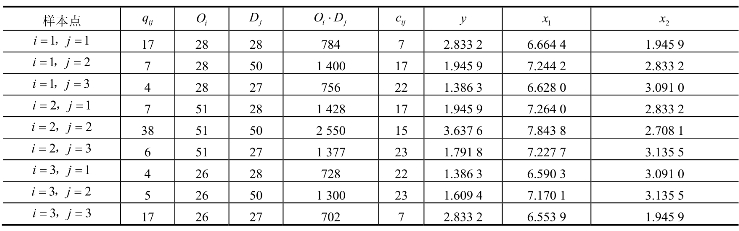
采用最小二乘法对九个样本数据进行标定，得出a0=-0.208 4，a1=1.173，a2=-1.455，则获得的二元线性回归方程为

y=-2.028+1.173x1-1.455x2

通过a0=lnα，a1=β，a2=-γ，可得α=0.124，β=1.173，γ=-1.455，即标定的重力模型为

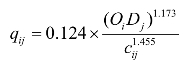
（2）利用已标定重力模型求解分布交通量：

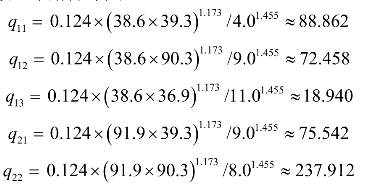
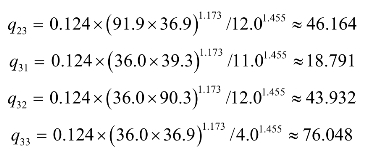
第一次计算得到的OD表如表7-12所示。

表7-12　第一次计算得到的OD表

（3）重新计算。

（4）通过无约束重力模型计算得到的OD表不满足出行分布的约束条件，因此还要用其他方法继续进行迭代，这里采用平均增长系数法进行迭代计算，计算结果如表7-13～表7-15所示。

表7-13　用平均增长系数法第一次迭代计算OD表

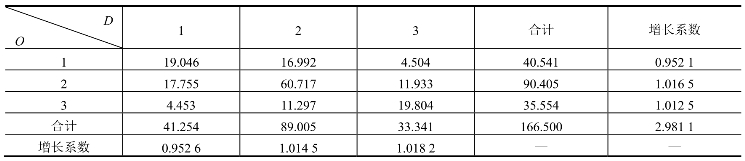
表7-14　用平均增长系数法第二次迭代计算OD表

表7-15　用平均增长系数法第三次迭代计算OD表

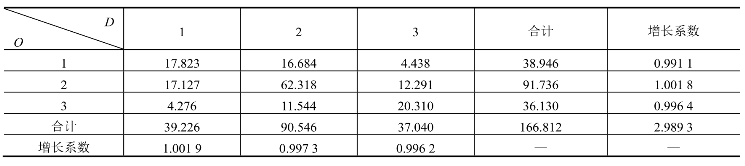
（5）第三次迭代之后，满足设定的收敛条件ε=1%，停止迭代，第三次迭代计算后得OD表，（表7-15）就为最终预测的OD表。

2）单约束重力模型

（1）乌尔希斯重力模型。此模型只满足式（7-26），即出行发生约束重力模型，其表达式为

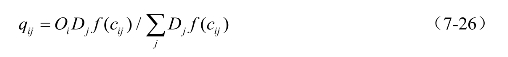
式中： f (cij)——交通阻抗函数，常用形式；

γ——待定系数。

以为例进行参数标定，待定系数γ根据现状OD调查资料拟合确定，一般可采用试算法等数值方式，以某一指标作为控制目标，通过用模型计算和实际调查所得指标的误差比较确定。其计算过程：先假定一个γ值，利用现状OD统计资料所得Oi、Dj及cij代入式（7-26）中进行计算，所得出的计算交通分布称为GM分布。GM分布的平均行程时间采用下式计算：

GM分布与现状分布的每次运行的平均行程时间之间的相对误差为。当交通按GM分布与按实际分布每次运行的平均相对误差不大于某一限定值（常用3%）时，计算即可结束。当误差超过限定值时需改动待定系数γ，进行下一轮计算。调整方法为如果GM分布的大于现状分布，可增大γ值；反之，则减小γ值。＇

（2）交通公路局重力模型（B.P.R模型）为

式中：kij——调整系数，其计算公式为

式中：λij——i小区到j小区的实际分布交通量与计算交通分布量之比；

Yij——i小区到j小区的实际分布交通量与i小区的出行发生量之比。

此模型与乌尔希斯重力模型相比，引进了交通调整系数kij。计算时，用于乌尔希斯重力模型相同的方法试算出待定系数γ，然后计算qij，最后计算kij。

这两种模型均满足，因此称为单约束重力模型。

用上述两种重力模型进行交通分布预测时，首先将预测的交通产生量和吸引量，以及将来的交通阻抗参数代入模型进行计算。通常计算出的交通吸引量与给定的交通吸引量并不相同，因此需要进行下一步迭代计算。

3）双约束重力模型

同时满足守恒条件的a是不存在的，因此，将重力模型修改为如下形式：

式中：。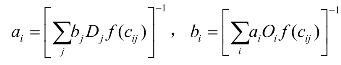

此模型为双约束重力模型。

下面以幂指数交通阻抗函数为例计算。

（1）令m=0，m为计算次数。

（2）给出γ（可以用最小二乘法求出）。

（3）令，求出。

（4）求出。

（5）收敛判定，若满足下式则计算结束；反之，令m+1=m。返回步骤（2）重新计算，公式为