交通生成（即发生与吸引预测）预测是交通需求四阶段预测中的第一阶段，是交通需求分析工作中最基本的部分之一，目标是求得各个对象地区的交通需求总量，即交通生成量（Trip Generation），进而在总量的约束下，求出各交通小区的发生交通量（Trip Productions）与吸引交通量（Trip Attraction）。出行的发生、吸引与土地利用的性质和设施规模有密切的关系。发生与吸引交通量预测精度将直接影响后续预测阶段乃至整个预测过程的精度。

图7-2所示为交通小区i的发生交通量和交通小区j的吸引交通量。Oi表示小区i的发生交通量（由小区i出发到各小区的交通量之和）；Dj表示小区j的吸引交通量（从各小区来小区j的交通量之和）。

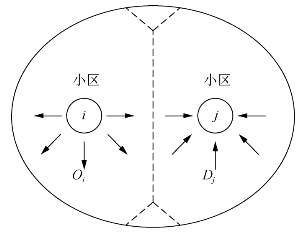
图7-2　交通小区出行的发生与吸引示意图

小区i的吸引交通量和小区j的发生交通量以此类推。发生与吸引交通量的预测方法分为原单位法、增长率法、函数法和交叉分类法。本节仅介绍前三种方法。

1. 原单位法

利用原单法预测发生和吸引交通量时，首先需要分别计算发生原单位和吸引原单位，然后根据发生原单位和吸引原单位与人口面积等属性的乘积预测发生与吸引交通量的值，可用式（7-1）表示：

式中：Oi——小区i的发生交通量；

b——某出行目的的原单位出行发生次数[次/(日·人)]；

x——常住人口、白天人口、从业人口、土地利用类别、面积等属性变量；

Dj——小区j的吸引交通量；

c——某出行目的的单位出行吸引次数[次/(日·人)]；

i，j——交通小区。

【例7-1】表7-1所示为各小区现在的出行发生量和吸引量。在常住人口原单位不变的情况下，采用原单位法预测其将来的出行生成量。

表7-1　各小区现在的出行发生量和吸引量 　（单位：万次/日）

【解】根据表7-1中的数据，可得

现状出行生成量T=28.0+51.0+26.0=105.0(万次/日)。

现状常住人口N=11.0+20.0+10.0=41.0(万人)。

将来常住人口M=15.0+36.0+14.0=65.0(万人)。

常住人口原单位T/N=105.0/41.0≈2.561[次/(日·人)]。

因此，将来的生成交通量。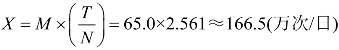

由于人们在对象区域内的出行不受区域内小区划分影响，因此交通生成量的原单位与发生、吸引的原单位比较，具有时间序列稳定的特点。

如上所述，将原单位视为不随时间变动的量，而直接使用居民出行调查结果。然而，原单位因交通参与者的个人属性（年龄、性别、职业、汽车拥有与否等）不同而变动。

一般来说，在交通需求预测时，要求各小区发生交通量之和与吸引交通量之和相等，并且各小区的发生交通量和吸引交通量之和均等于交通生成量。如果它们之间不满足上述关系，则可采用如下方法进行调整：

（1）总量控制法。在实际计算中，各个交通小区的推算量的误差是不可避免的，从而造成总量的误差，为此，应当根据区域的交通生成总量推算得到的各个小区的发生量进行校正。

假设交通生成总量T是由人口P与生成原单位p而得到的，则

如果交通生成总量T与总发生量有明显的误差，则可以将Oi修正为

保证T与总吸引交通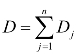也相等，才能使发生交通量之和、吸引交通量之和及交通生成总量三者全部相等，为此Dj修正为

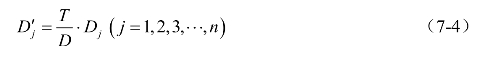
（2）调整系数法。在出行生成阶段，要求满足所有小区出行发生总量要等于出行生成总量。当上述条件不满足时，一般认为所有小区出行发生总量更可靠一些。从而，可将吸引总量乘以一个调整系数f，这样可以确保出行吸引总量等于出行发生总量。

【例7-2】 假设各小区的发生与吸引原单位不变，试用例7-1的数据求出将来的发生与吸引交通量。

【解】（1）求出现状发生与吸引量的原单位。

小区1的发生原单位：28.0/11.0=2.545次/(日·人)。

小区1的吸引原单位：28.0/11.0=2.545次/(日·人)。

同理，可以计算其他交通小区的原单位，结果如表7-2所示。

表7-2　现状各小区发生与吸引的原单位　（单位：万次/日）

（2）计算各交通小区将来的发生与吸引交通量。

小区1的发生交通量：15.0×2.545=38.175(万次/日)。

小区1的吸引交通量：15.0×2.545=38.175(万次/日)。

同理，小区2和小区3的发生与吸引交通量计算结果如表7-3所示。

表7-3　各小区未来的出行发生与吸引交通量　（单位：万次/日）(www.daowen.com)

调整计算。由上面结果可知，各小区发生交通量之和不等于其吸引交通量之和，所以，需要进行调整计算。调整的目标是使得上述两者相等，即满足：

调整方法可以采用总量控制法，即使各小区发生交通量之和等于其吸引交通量之和，且都等于将来的交通生成总量166.5万次/日。根据总量控制法的式（7-3）和式（7-4）可推导得

按上式计算后结果如下：

各区未来的发生与吸引交通量如表7-4所示。

表7-4　各区未来的发生与吸引交通量　（单位：万次/日）

由上述可以看出，调整以后，各小区的发生与吸引交通量之和相等，均等于交通生成总量166.5万次/日。

如前所述，在交通需求预测时，要求发生交通量与吸引交通量相等。对于例7-2，调整后的同一小区的发生与吸引交通量不相等的情况，还可以继续调整。调整方法是取同一小区发生与吸引交通量的平均值，这里省略此步骤。

2. 增长率法

增长率法考虑了原单位随时间变动的情况，它是用其他指标的增长率乘以原单位，求出将来生成交通量的方法，即

式中：Fi——发生和吸引交通量的增长率。

例如，Fi=αi⋅βi，其中，αi=目标年度小区i的预测人口/基准年度人口小区i的人口；βi=目标年度小区i的人均车辆拥有率/基准年度人口小区i的人均车辆拥有率。

增长率法的特点可以解决原单位法和函数法难以解决的问题，它通过设定交通小区的增长率，可以反映土地利用的变化引起的人们出行的变化，以及对象区域外交通小区的发生与吸引交通量。对于后者，由于原单位法和函数法都基于实际调查数据的方法，而对象区域外的交通小区没有实际测量数据和预测目标年度自变量数据，因此应选用增长率法。增长率法可以预测对象区域外小区的将来交通量，如可以设定：

式中：Fi——对象区域外交通小区i的发生、吸引交通量的增长率；

Ri——对象区域外交通小区i的常住人口增长率；

R——对象区域内全体的常住人口增长率。

【例7-3】 设某区域现在共有500户家庭，其中250户每户拥有1辆小汽车，另外250户没有小汽车，有汽车家庭出行生成原单位为6次/日，无汽车家庭为2.5次/日。假设未来所有家庭都有1辆小汽车，家庭收入和人口数不变，用增长率法求出规划年的出行发生量Ti。

【解】根据出行生成原单位，易得该区域现在的出行量为假设未来所有家庭都有1辆小汽车，家庭收入和人口数不变，则增长系数Fi为

T=250×2.5+250×6=2 125(次/日)

式中：——该区域未来的汽车保有率；

——该地区现在的汽车保有率。

因此，得该区域未来出行量为Ti=2×2 125=4 250(次/日)。

可见，增长系数法比较简单，是早期城市交通规划采用的方法之一。经验得出该方法计算的结果偏大，西方一些规划专家们推荐用此方法预测研究区域外部的出行。

3. 函数法

函数法是利用函数式预测将来不同目的的原单位，是发生和吸引交通量预测中常用的方法之一。函数法中多采用多元回归分析法，所以有时也将其直接称为多元回归分析法，其中模型如下。

式中：b，c——回归系数；

p——出行目的；

x——自变量，常取的变量有交通小区内平均收入、平均汽车保有率、家庭数、人口、就业人数、土地利用面积等。

使用多元回归分析法，一般先用实际调查数据和最小二乘法得出回归系数b和c，然后将各交通小区预测目标年的自变量值代入式（7-9）、式（7-10），求出各交通小区的发生和吸引交通量。

假设得到的关系式为

式中：Ti——交通小区i的上下班出行次数；

x1i——交通小区i的家庭数；

xi2——交通小区i的就业人口数；

xi3——交通小区i的汽车保有量；

xi4——交通小区i与市中心的距离。

由此可选择x1i、x2i、x3i、x4i目标年度的预测值，求得目标年度的Ti。

选用多元线性回归法时，应注意自变量之间的相互独立性，该方法不能表现因土地利用的变化带来的人们出行行为的变化及交通条件的改善引起人们出行能力的增强。