图5-18所示为由四车道路段过渡到三车道路段的半幅平面示意图。由图5-18可以看出，在四车道的路段（即原路段）和三车道的路段（即瓶颈段），车流都是各行其道、井然有序的，而由四车道向三车道过渡的那段路段内，车流出现了拥挤、紊乱，甚至阻塞。这是因为车流在即将进入瓶颈段时会产生一个方向相反的波，就像声波碰到障碍物时的反射，或管道内的水流突然受阻时的后涌。这个波导致在瓶颈段之前的路段车流出现紊流现象。

图5-18　瓶颈处的车流波

1. 基本方程

为讨论方便起见，取图5-19所示的计算图示。假设一分界线s将交通流分割为A、B两段。A段的车流速度为V1，密度为K1；B段的车流速度为V2，密度为K2；分界线s的移动速度为Vw，假设沿路线按照所画的箭头x正方向运行，速度为正，反之为负。

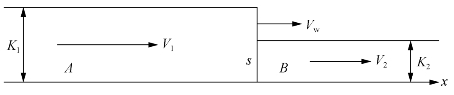
图5-19　两种密度的车流运行状况

则在时间t内横穿s分界线的车数N为

即

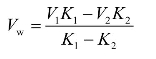
令A、B两部分的车流量分别为q1、q2，则根据宏观交通流模型Q=KV可得

于是，式（5-73）变为

当q1＞q2，K1＜K2时，Vw为负值，表明波的方向与原车流流向相反。此时，在瓶颈过渡段（图5-18）内的车辆被迫后涌，开始排队，出现阻塞。有时Vw可能为正值，表明此时不致发生排队现象，或已有的排队开始消散。

若A、B两区车流量与交通密度大致相等，则可以写成

因此，可得传播小紊流的速度为

至此，以上分析尚未触及区间平均车速V1及V2与密度K1及K2之间的任何具体关系。如果采用线性的速度与密度的关系式，即

设ηi=Ki/Kj，则

式中：η1，η2——分界线s两侧的标准化密度。

将以上关系代入式（5-73）得波速为

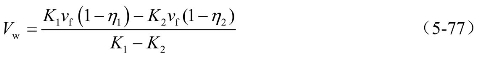
从式（5-76）得到η1和η2的关系式，可用来简化式（5-77）。利用交通流密度不连续分界线两侧的标准化密度可描述波速大小，即

2. 交通密度大致相同的情况

Lightill和Whitham认为：如果在分界线s两侧的标准化密度η1与η2相等，如图5-20所示，s左侧的标准化密度为η，而s右侧的标准化密度为（η+η0），这里的η+η0≤1，在此情况下，设：

且

式中，η0忽略不计。把上式代入式（5-78），则此连续的波就以下列速度传播：

3. 停车产生的波(www.daowen.com)

对于车流的标准化密度为η2、以区间平均车速V1行驶的车辆，假设下式成立：

在道路上，位置x=x0处，因红灯停车，车流立即呈现饱和的标准化密度η2=1，如图5-21所示。线s左侧，车流仍为原来的密度η1按平均速度V1继续进行。将η2=1代入式（5-78），得到停车产生的波的波速为

式（5-80）说明，由于停车产生的波，以Vw的速度向后方传播。如果信号在x=x0处变为红灯，则经过ts以后，一列长度为vfη1t的汽车就要停在x0之后。

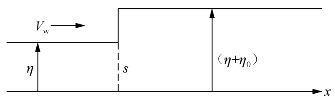
图5-20　交通密度微小的不连续性

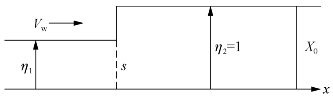
图5-21　停车产生的波

4. 发车产生的波

现在来讨论一列车辆起动（发车）所产生的波的性质。假设t=0时，一列车已停在位于x=x0处的信号灯后边。因为这列车停着，所以具有饱和密度η1=1，如图5-22所示。如果在t=0时，x=x0处变为绿灯，车辆以速度V2起动，此时，停车一方（s线左侧）的交通流密度仍为饱和密度η1=1，而η2可以从式V2=vf(1-η2)求得，即

代入式（5-78），则

所以，一旦车队开始运行（发车），就产生发车波，该波从x0处以（vf-V2）的速度向后传播。由于发车速度V2一般很低，因此可以看作以vf速度传播。

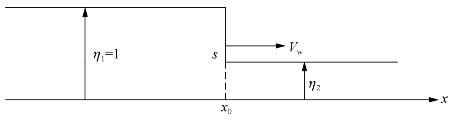
图5-22　发车产生的波

【例5-7】 车流在一条六车道的公路上畅通行驶，其速度V为80 km/h。路上有座四车道的桥，每车道的通行能力为1 940辆/h，高峰时车流量为4 200辆/h（单向）。在过渡段的车速降至22 km/h，这样持续1.69 h，然后车流量减到1 956辆/h（单向）。

（1）试估计1.69 h内桥前的车辆平均排队长度；

（2）估计整个过程的阻塞时间。

【解】（1）计算平均排队长度。

桥前高峰时车流量为4 200辆/h（单向），其每条车道高峰时车流量和通行能力之比约为0.72，交通流能够保持畅通行驶，车道内没有阻塞现象，因此桥前来车的交通流密度K1为

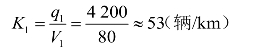
在过渡段，由于该处只能通过1 940×2=3 880（辆/h），而现在却有4 200辆/h的交通需求强度，故在过渡段出现拥挤；过渡段的交通流密度K2为

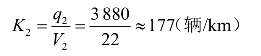
得。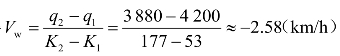

表明此处出现排队的反向波，其波速为2.58 km/h，因距离为速度与时间的乘积，且开始时刻排队长度为0，故1.69 h末的排队长度为（2.58×1.69）km，此过程中排队长度均匀变化，故此处的平均排队长度为

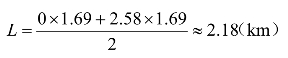
（2）计算阻塞时间。

高峰过去后，排队即开始消散，但阻塞仍要维持一段时间。因此，阻塞时间应为排队形成时间（即高峰时间）与排队消散时间之和。

排队消散时间t′：已知高峰后的车流量q3=1 956 辆/h＜3 880 辆/h，表明通行能力已有富裕，排队开始消散，则排队车辆数为

（q1-q2）×1.69=(4 200-3880)×1.69 ≈54（1辆）

疏散车辆数为

q3-q2=1956-3880=-192（4辆/h）

排队消遣时间为

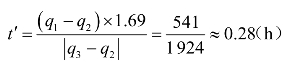
阻塞时间为

t=t′+1.69=0.28+1.69=1.97（h）