M/M/1系统中，排队等待接受服务的通道只有一条，因此，又称单通道服务系统。

设顾客平均到达率为λ，则两次到达之间的平均时间间隔为1/λ。假设从单通道接受服务后出来的输出率（即系统的服务率）为μ，则平均服务时间为1/μ。比值ρ =/λ μ称为交通强度或利用系数。如果ρ＜1，则每个状态都会按一定的概率反复出现。若ρ ≥1，则排队长度会越来越长，系统状态是不稳定的。因此，只有ρ＜1，即λμ＜时，系统才可以保持稳定，通道内的排队顾客才能够消散。

下面给出M/M/1系统常用的一些计算公式。

系统中没有顾客的概率为

系统中有n个顾客的概率为

排队系统中顾客的平均数为

排队系统中顾客数的方差为

平均排队长度为

顾客的平均数和顾客数的方差σ2与ρ的关系，可由图5-14和图5-15看出，当交通强度ρ＞0.8时，平均排队长度和方差迅速增加，即系统不稳定性增强。

平均非零排队长度为

排队系统中的平均消耗时间为

排队中的平均等待时间为

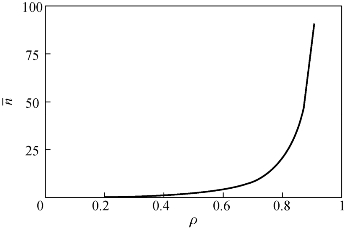
图5-14　系统顾客数和交通强度ρ关系图

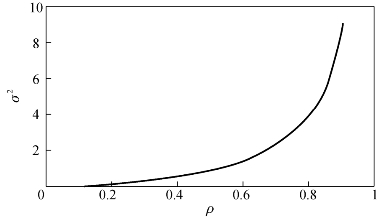
图5-15　顾客数方差σ2和交通强度ρ关系图

【例5-4】 一个停车库出口只有一个门，在门口向驾驶员收费并找零钱。假设车辆到达服从泊松分布，参数λ为120辆/h，收费平均持续时间为15 s，服从指数分布，试求收费空闲的概率、系统中有n辆车的概率、系统中平均车辆数、排队的平均长度、平均非零排队长度、排队系统中的平均消耗时间、排队中的平均等待时间。

【解】由题意可知，这是个M/M/1系统，并且λ=120辆/h，μ=3 600/15=240（辆/h）。(www.daowen.com)

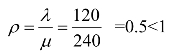
所以，系统稳定。

由式（5-55）可求得系统中没有车辆的概率为

由式（5-56）求得系统中有n辆车的概率为

由式（5-57）可得系统中的平均车辆数为

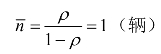
由式（5-59）求得平均排队长度为

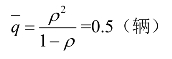
由式（5-60）求得平均非零排队长度为

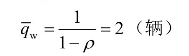
由式（5-61）求得系统中的平均消耗时间为

由式（5-62）求得排队中的平均等待时间为

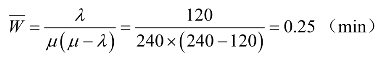
【例5-5】 拟修建一个服务能力为120辆/h的停车场，只有一个出入通道。据调查每小时有72辆车到达，假设车辆到达服从泊松分布，每辆车服务时间服从负指数分布，如果出入通道能容纳5辆车，问是否合适？

【解】这是个M/M/1排队系统。由题意知：

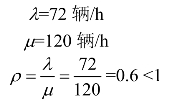
所以，系统稳定。由式（5-57）可求得系统中的平均车辆数为

因此，系统中的平均车辆数小于通道容纳的能力，故合适。也可计算系统中车辆数超过5辆的概率。由式（5-56）可得

所以，系统中车辆数超过5辆的概率为

由计算结果可以看出，系统中车辆数超过5辆的可能性只有5%，所以该通道的容量是合适的。