1. 模型描述

跟驰模型是刺激-反应方程的一种形式，反应就是交通流中驾驶员对直接在它前面运行车辆的反作用。交通流中连接驾驶员反应的是与t时刻的刺激大小成比例的加速或减速，并且在t+T时刻开始。

该模型的基本方程式如下：

假设跟驰中驾驶员保持后随车与前导车的距离为hs(t)，如果第一辆车紧急停车，第二辆车停下来就不会碰撞第一辆车，驾驶员的反应时间为T，该时间是从前车驾驶员开始停车的时间t起直到第二辆车驾驶员开始停车操作止，在反应时间内，车速不变，两车在t时刻的相对位置如图5-10的上部所示。n为前导车，n+1为后随车。t时刻，前导车开始制动，两车停止后的相对位置如图5-10下半部所示。

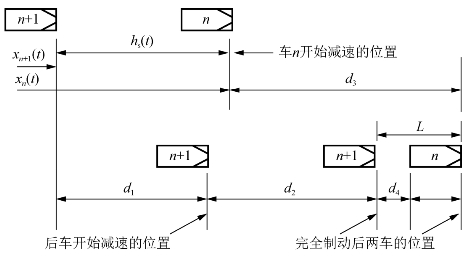
图5-10　跟驰关系图

L——停止时的车头间距（m）；d1——车辆n+1在反应时间t内行驶的距离（m）；d2——车辆n+1从制动到完全停止所行驶的距离（m）；d3——车辆n从制动到完全停止所行驶的距离（m）；d4——两车停车后的缓冲距离（m）；xn（t）——第n辆车在t时刻的位置（m）

因此，在t时刻，前车突然停车而不发生碰撞，所要求的车头间距为

确定车辆的速度为

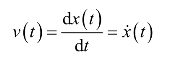
加速度为

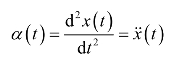
则

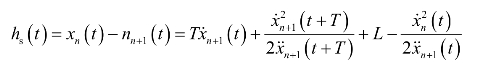
假设两车停下来所需的加速度和距离都相等，即d2=d3，车头间距hs为

即在反应时间t内，后随车所行驶的距离d1加上停车时的车头间距L。上式对t进行微分，则

因此，在t+T时刻，后车的加速度就成为

式（5-50）是在假定两车停下来所需的加速度和距离都相等的情况下推导出来的。实际情况要比这个假设所限定的条件复杂得多，为了适应更一般的情况，式（5-50）可以修改为

式中：λ——反应强度系数（1/s）。

这里λ不再是简单的敏感度，而是与驾驶员动作的强弱程度直接相关的系数。该式表明后车的反应与前车的刺激成正比，因此称为线性跟驰模型。

2. 模型的稳定性

在研究跟驰特性时，车队车辆的稳定性问题是很重要的。如果驾驶员的特性有改变，或车辆中的机械部件或信号灯有变化，则一个重要的工作就是确定系统是否稳定。稳定有两层意思，一是指前后两车之间的距离变化是否稳定，例如，车间距的摆动，若摆动大则不稳定，摆动越小越稳定，称为局部稳定性；二是指前车向后面各车传播速度的变化，如扩大其速度振幅，则不稳定，如振幅逐渐衰弱，则稳定，称为渐进稳定性。

线性跟驰模型是一个较复杂的二阶微分方程，利用拉普拉斯变换求解除该微分方程，并推导出如下关系：

(www.daowen.com)

式中：C——表示车间距摆动特性的数值，该值越大，表示车间距的摆动越大，该值越小表示车间距的摆动趋近于零；

λ——含义同式（5-51），其值大，表示反应过分强烈；

T——反应时间（s）。

局部稳定：表5-1列出了各种C值时车间距的摆动情况。从表5-1中可以看出，随着C值的增大，车间距逐渐变得不稳定。这是因为如果对出现的事件，反应时间越长，反应太强烈（λ大，表现在节气门过大，制动踏板踏得太重），则在做出反应时，情况可能偏离实际需要。

表5-1　线形跟驰模型的车间距摆动情况

如图5-11所示，当C=0.50时，间距值的摆动衰减很快；当C=0.80时，其摆动逐渐减小；当C=1.57时，摆动停止衰减，其间距基本稳定；当C=1.60时，摆动幅度逐渐增大。可见，C=1.57为线性跟驰模型中车头间距从稳定到非稳定的临界值。

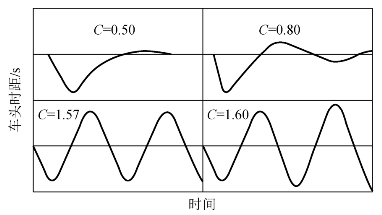
图5-11　前后相邻两车间的车头时距变化

逐渐稳定：一列处于跟驰状态的车队仅当C＜0.50时，才是逐渐稳定的。

与局部稳定相比较，这里C=0.50时，车头间距的摆动衰减很快。头车运行中的扰动是以1/ λ（s/辆）的速率沿车队向后传播。当C＞0.50时，将增大变动幅度传播，增大了车辆间的干扰，当干扰的幅度增大到使车间距小于一个车长时，发生追尾事故。图5-12所示为一列有八辆车的车队，在不同的C值时的车头间距。车辆间初始间距为21 m，当头车减速后又加速到原来的速度，图中曲线的变化表示扰动沿车向后传播的情况。

图5-12　不同C值时车队内车头间距变化

3. 从跟驰理论到交通流模型

线性跟驰模型的特点是简便和对稳定性分析的敏感性，但它的明显缺点是后车的反应（加速度）仅考虑了两车相对速度的影响，而与车间距无关。1959年，通过Gazis等人的研究，采用灵敏度系数λ与车头间距成反比例关系，得到非线性跟驰模型，即

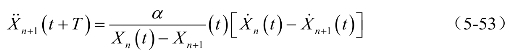
式中：α——比例常数（km/h），；

vm——临界速度（km/h）；

vf——自由流速度（km/h）。

表5-2所示为参数α的实验结果。

表5-2　非线性跟驰模型α 的试验结果

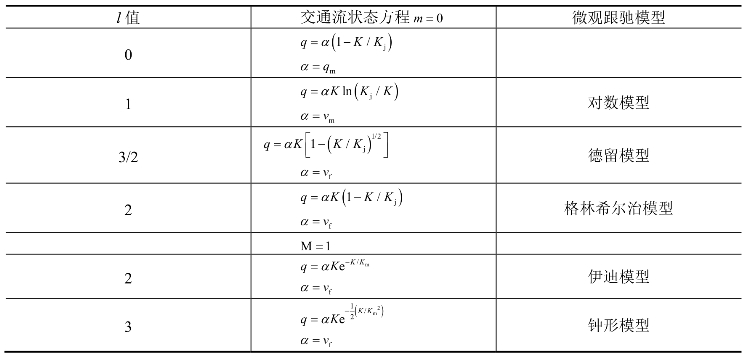
在非线性跟驰模型的发展过程中，很多人根据不同的假设提出了不同的模型，而在1961年，Gazis又提出了跟驰模型的一般公式，即

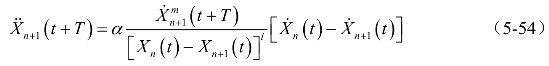
式中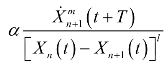：——灵敏度；

m，l——常数。

假设一车流中，车头以恒速前进，而各跟随车辆以同样的速度前进，与前一辆车的间距由驾驶员的感觉和驾驶员对安全跟随距离的判断来决定。车队沿车行道以稳定状态行驶，对此可以观测流率q、密度K及速度v。Gazis证明：从微观的跟驰理论建立的运动规律，通过积分运算可得到宏观的交通流方程，根据速度方程边界条件求解，可确定积分常数。Gazis等人利用实测交通流数据，对各种m和l值各种组合下的稳定交通流状态进行了综合讨论（表5-3），建立了一组交通流微观跟驰模型和宏观模型之间的对应关系。

表5-3　微观跟驰模型与宏观交通流模型的对应表