车流到达的统计规律除了可用离散型分布来描述外，还可用车头时距的分布来描述。连续型分布是描述事件之间时间间隔分布规律的模型，常用来描述交通流中前后车辆的车头时距分布情况。

1. 负指数分布

负指数分布可用于描述车头时距的概率分布。对于交通流来说，车头时距可能相等，也可能不相等。由于泊松分布着眼于一定时间间隔的车辆到达数，因此可以通过泊松分布的规律来推出前后车辆之间的车头时距。若车辆到达符合泊松分布，则车头时距就是负指数分布，反之也成立。

1）基本公式

由式（5-10）可知，在计数间隔t内没有车辆到达（k=0）的概率为

式（5-31）表明，在具体的时间间隔t内，如无车辆到达，则前辆车到达和后辆车到达之间的车头时距至少有t s，P(0)也是车头时距h等于或大于t s的概率，于是有

则车头时距小于t的概率为

若Q表示小时交通量，则/3 600Qλ=（辆/s），式（5-32）可以写成

式（5-34）中的Qt/3 600是到达车辆数概率分布的平均值。若令M为负指数分布的均值，即平均车头时距，则应有

负指数分布的方差为

用样本的均值m代替M、样本的方差S2代替D，即可算出负指数分布的参数λ。

此外，也可用概率密度函数来计算。负指数分布的概率密度函数为

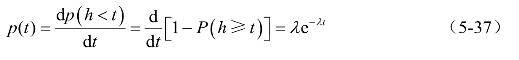
2）适用条件

负指数分布适用于车辆到达是随机的、有充分超车机会的单列车流和密度不大的多列车流的情况。通常认为，当每小时每车道的不间断车流量等于或小于500辆时，用负指数分布描述车头时距时符合实际的。

由式（5-37）可知，负指数分布的概率密度函数是随车头时距t单调递减的，这说明车头时距越小，其出现的概率越大。这种情况在限制超车的单列车流中是不可能出现的，因为车头间距至少应为一个车身长，车头时距必须有一个大于零的最小值τ，否则会导致车辆头尾相接，这就是负指数分布的局限性。

因此，在观测统计时，往往略去最小车头间隔，使计算结果合理。对负指数分布加以变换称为移位负指数分布。

2. 移位负指数分布

1）基本公式

为克服负指数分布的车头时距越趋于零，其出现概率越大这一缺点，使数学模拟规律更接近实际交通流运行状况，可将负指数分布曲线从原点O沿t轴向右移一个最小的间隔长度τ（根据调查数据确定，一般为1.0～1.5 s），得到移位负指数分布曲线，它能更好地拟合观测数据。

移位负指数分布的分布函数为

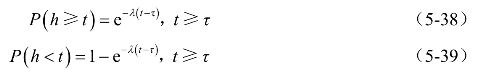
其概率密度函数为

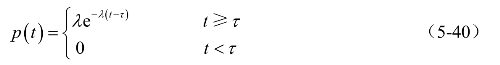(www.daowen.com)

均值和方差分别为

用样本均值m代替M，样本方差S2代替D，就可算出移位负指数分布的两个参数λ和τ。

2）适用条件

移位负指数分布适合描述限制超车的单列车流车头时距分布和低流量时多列车流的车头时距分布。

移位负指数分布的概率密度函数是随（t-τ）的值单调递减的，即移位负指数分布的车头时距，越接近τ其出现的可能性越大，但这在一般情况下不符合驾驶员的心理习惯和行车特点。从统计角度看，具有中等反应强度的驾驶员占大多数，他们行车时在安全条件下保持较短的车间距离（前车车尾与后车车头之间的距离，不同于车头间距），只有少部分反应特别灵敏或较冒失的驾驶员才会不顾安全地去追求更短的车间距离。因此，车头时距分布的概率密度曲线一般总是先升后降的。为了克服移位负指数分布的这种局限性，可用更通用的连续型分布，如韦布尔分布、爱尔朗分布、皮尔逊Ⅲ型分布、对数正态分布、复合指数分布等，这里仅介绍前两种分布。

3. 韦布尔分布

1）基本公式

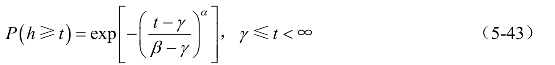
式中，β、γ、α为分布参数，取正值，且βγ＞，γ称为起点参数，α称为形状参数，β称为尺度参数。韦布尔分布的概率密度函数为

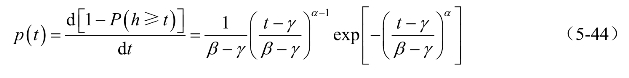
图5-8所示为γ=0、β=1的韦布尔分布概率密度曲线，曲线的形状随着参数α的改变而变化，可见韦布尔分布的适用范围是比较广泛的。当α=1时，即为负指数分布；当α=2或3时，与正态分布十分近似。当使用韦布尔分布拟合数据时，可根据观测数据查阅相关的韦布尔分布拟合用表，确定所要使用的韦布尔分布的具体形式。

2）适用条件

韦布尔分布使用范围较广，交通流中的车头时距分布、速度分布等一般都可用韦布尔分布来描述。实践表明，对具有连续型分布的交通流参数进行拟合，韦布尔分布常具有与皮尔逊Ⅲ型分布、对数正态分布、复合指数分布同样的效力。韦布尔分布的拟合步骤并不复杂，其分布函数也比较简单，这是皮尔逊Ⅲ型分布所不具备的优点，这个优点给概率计算带来了很多便利。此外，韦布尔分布随机数的产生也很简便。因此，当使用最简单的负指数分布或移位负指数分布不能拟合实测的数据时，选用韦布尔分布拟合是最好的方法。

图5-8　韦布尔分布概率密度曲线

4. 爱尔朗分布

1）基本公式

常用的爱尔朗分布可写成如下形式：

爱尔朗分布也是较为通用的描述车头时距分布、速度分布等交通流参数分布的概率模型。根据分布函数中参数l的改变而有不同的分布函数。

当1l=时，式（5-45）简化成负指数分布；当l→∞时，式（5-45）将产生均一的车头时距。实际应用时，l值可由观测数据的均值m和方差S2用下式估算，且四舍五入取整数：

爱尔朗分布的概率密度函数为

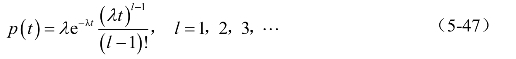
图5-9所示为l=1、2、4时的概率密度曲线。

图5-9　λ固定时，与不同l值对应的爱尔朗分布概率密度曲线

2）适用条件

爱尔朗分布中，参数l可以反映畅行车流和拥挤车流之间的各种车流条件。l越大，说明车流越拥挤，驾驶员自由行车越困难。因此，l值是非随机性程度的粗略表示，非随机性程度随着l值的增加而增加。