连续流是指没有外部固定因素(如交通信号)影响的不间断交通流,如高速公路的基本路段、双车道和多车道的交通流。
1. 三参数的相互关系
连续交通流的特性可用交通流量、平均车速和交通流密度三个参数予以描述。平均车速和交通流密度反映交通流从道路获得的服务质量,交通量可以度量交通设施的负荷程度。交通流量、平均车速、交通流密度三个参数是描述交通流基本特征的主要参数,这三个参数之间相互联系、相互制约。为了研究它们之间的关系,专家学者们将物理学中的流体理论引入交通流的研究之中,将交通流近似看作由交通体组成的一种粒子流体,就像其他流体一样,可以用流体力学和数学的有关理论,建立相关的描述交通流特征的数学模型。但是,应该承认公路上交通流的情况受很多因素(如人、车、路、环境等)的影响,而且许多因素是不恒定的。因此,要通过设立某些假设条件将交通流模拟为流体进行研究。
假设交通流为自由流。在长度为L的路段上有连续行驶的N辆车,其平均速度为![]() ,如图5-1所示。由三个参数的定义可知:
,如图5-1所示。由三个参数的定义可知:
L路段上的交通流密度为![]() 。
。
N号车通过A断面所用的时间为![]() 。
。
N号车通过A断面交通量为![]() 。
。
将以上各式整理得
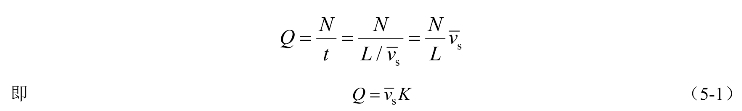
式中:Q——流量(辆/h);
![]() ——区间平均车速(km/h);
——区间平均车速(km/h);
K——密度(辆/km)。
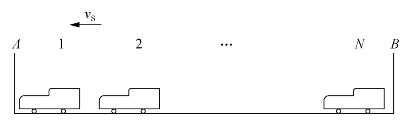
图5-1 三参数计算图
式(5-1)表示的关系是一种三维空间关系,用三维坐标表示的这种空间曲线,如图5-2所示。三维曲线图投影到三个二维坐标系中即速度-密度、交通流量-密度、速度-交通流量之间的关系图,如图5-3所示。图5-3(a)所示为以格林希尔治的单段式速度-线性关系模型为依据绘制的;图5-3(b)和(c)则是以(a)中的关系模型为基础,根据式(5-1)推导出的。
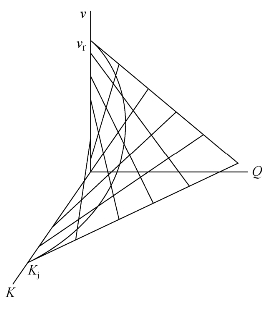
图5-2 Q=v·K关系三维曲线图
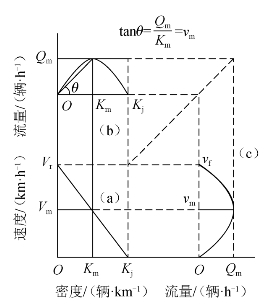
图5-3 速度-密度、交通流量-密度和速度-交通流量关系图
在图5-3中,需要注意交通流特性参数中的一些特殊值。
自由流速度(Free-Flow Speed)vf:又称畅行速度,一辆车在无其他车辆干扰的条件下通过某一区段的最高车速。
阻塞密度(Jam Density)Kj:密度持续增加使流量趋近于0时的密度,或指停车排队的密度。
临界密度(Critical Density)Km:流量逐渐增大,接近或达到道路通行能力时的密度。临界密度又称最佳密度。
临界速度(Critical Speed)vm:流量逐渐增大,接近或达到道路通行能力时的速度。
最大流量Qm:路段上能够通行的最大流量。
在该模型中,流量为0时有两种情况,第一种是道路上没有车辆通过,此时的密度为0,车辆可以以“自由流速度”行驶。第二种情况是交通出现了阻塞,所有车辆都被迫停了下来,所以没有车辆通过观察点,此时的密度为阻塞密度。
密度-流量和速度-流量曲线的最高点是饱和流量,这一点是不稳定的。当接近饱和时,交通流中可利用的空间变得越来越小,在达到饱和时,就没有空间可利用了,这时交通流密度达到临界密度。在这一时刻,交通流中任何混乱或意外事件的发生,都会产生连锁反应,从而使流量有所降低,甚至发生阻塞。所以,这一点的流量称为强制流或称不稳定流。
在格林希尔治假设下,主要变量的临界值很容易确定下来:临界速度是自由流速度的一半,而自由流速度是速度-密度曲线上速度的轴截距;临界密度是阻塞密度的一半,而阻塞密度是速度-密度曲线上密度的轴截距。饱和流量或最大流量可以由临界速度和临界密度得到。
2. 速度与密度的关系
在实践中,可以看到这样一种现象:当道路上的车辆增多、交通流密度增大时,驾驶员被迫降低车速。当交通流密度由大变小时,车速又会增加。这就说明速度和密度之间有一定的关系。
2026年,格林希尔治在对大量观测数据进行分析之后,提出了速度-密度的线性关系模型。

式中:vf——自由流速度;
Kj——阻塞密度。
这一模型简单直观。研究表明,在通常的交通流密度下,该模型与实测数据的拟合较好。
由图5-4可见,当K=0时,![]() ,即在交通量很小的情况下,车辆可以自由流速度行驶。当K=Kj时,
,即在交通量很小的情况下,车辆可以自由流速度行驶。当K=Kj时,![]() ,即在交通流密度很大时,车辆速度趋向于零。流量变化也可以用速度-密度图来说明,例如,已知C点的速度为vm,密度为Km,则流量Q=vmKm,它就是曲线下面的矩形阴影部分的面积。
,即在交通流密度很大时,车辆速度趋向于零。流量变化也可以用速度-密度图来说明,例如,已知C点的速度为vm,密度为Km,则流量Q=vmKm,它就是曲线下面的矩形阴影部分的面积。

图5-4 速度-密度关系图(https://www.daowen.com)
研究表明,当交通流密度很大或很小时,该模型与实际情况有一定偏差。后人对格林希尔治模型进行了改进。
当交通流密度很大时,可以采用格林伯格提出的对数模型:

式中:vm——临界速度。
当交通流密度很小时,可采用安德伍德提出的指数模型:
![]()
式中:Km——临界密度。
3. 流量与密度的关系
交通流的流量-密度关系是交通流的基本关系。根据格林希尔治模型及基本关系式,得

式(5-5)是二次函数关系,用图形表示为一条抛物线,如图5-5所示。
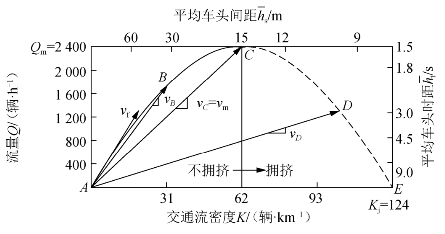
图5-5 流量-密度关系图
图5-5中C点代表最大流量Qm,相应的密度为Km。从这点起,流量随密度的增加而减小,直至达到阻塞密度Kj,此时流量Q=0。从原点A至曲线上的B、C和D点的箭头为矢量,这些矢量的斜率表示速度。通过A点且与曲线相切的矢量,其斜率为自由流速度vf。在流量-密度曲线上,密度比Km小的点表示不拥挤,密度比Km大的点表示拥挤状态。
从基本定义出发,可证明平均车头间距![]() 和平均车头时距
和平均车头时距![]() 分别为流量及密度的函数。假定车辆平均长度为6.1 m,在阻塞密度时,单车道上车辆间的平均间隔为1.95 m,因此,
分别为流量及密度的函数。假定车辆平均长度为6.1 m,在阻塞密度时,单车道上车辆间的平均间隔为1.95 m,因此,![]() ,由式(3-17),曲线上E点的阻塞密度值为
,由式(3-17),曲线上E点的阻塞密度值为
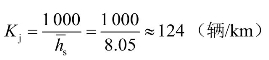
假定![]() ,根据式(3-18),曲线上C点的最大流量或最大通行能力为
,根据式(3-18),曲线上C点的最大流量或最大通行能力为
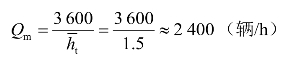
C点的临界密度Km可直接从图中看出,它等于62辆/km。
确定最大流量时的车速vm,只要计算出从原点A到C的矢量斜率,即vm=vC= 2 400 ÷62 =38.7(km/h)。
流量-密度曲线上,其他点的数值可以同样的方式求出。例如,B点是表示不拥挤情况下的一个典型点。从图5-5来看,B点的流量为1 800辆/h,密度为30辆/km,速度(AB矢量的斜率)为58 km/h。D点是表示拥挤情况下的一个典型点。从图5-5中可以看出,D点的流量为1 224辆/h,密度为105.6辆/km,速度(AD矢量的斜率)为11.6 km/h。
4. 流量与速度的关系
由式(5-2)可得

代入式(5-5)得

式(5-7)同样是一条抛物线,如图5-6所示,形状与流量-密度曲线相似。通常速度随流量增加而降低,直至达到最大通行能力的流量Qm为止。在曲线上拥挤的部分,流量和速度都降低。A、B、C、D和E点对应于流量-密度曲线和速度-密度曲线上相同的点。从原点E到曲线上各点矢量的斜率表示此点的密度的倒数1/K。在速度-流量曲线上,C点以上的部分表示不拥挤,而C点以下的部分表示拥挤状态。
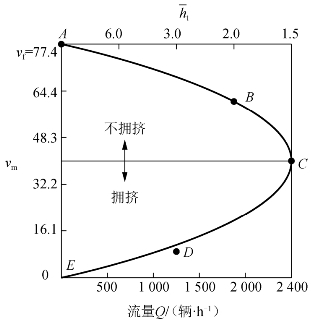
图5-6 流量-速度关系图
综上所述,由格林希尔治的假设所得到的各种模型可以看出,Qm、vm和Km是划分交通是否拥挤的重要特征值。当Q ≤Qm,K >Km,![]() 时,交通处于拥挤状态;当Q ≤Qm,K ≤Km,
时,交通处于拥挤状态;当Q ≤Qm,K ≤Km,![]() 时,交通处于不拥挤状态。
时,交通处于不拥挤状态。
【例5-1】 已知某公路上畅行速度vf=80 km/h,阻塞密度Kj=100辆/km,速度-密度关系为线性关系。试问:
(1)该路段上期望得到的最大流量是多少?
(2)此时所对应的车速是多少?
【解】(1)因为最大流量![]() ,所以
,所以
![]()
(2)当交通流量最大时,速度![]() ,所以
,所以
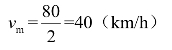
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






