根据以上分析，使用MATLAB进行仿真。仿真程序的流程图如图9-9所示。

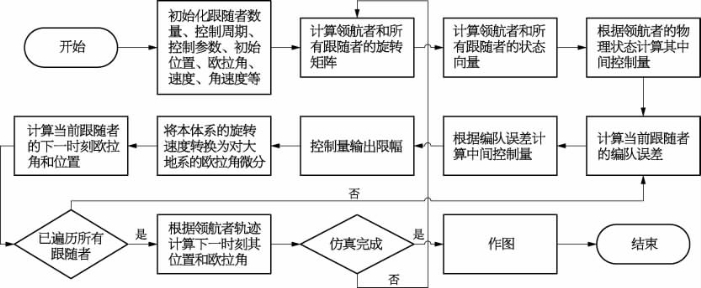
图9-9　协同运动控制器仿真流程图

需要说明的是，在仿真主循环的每一次中，我们得到的是在AUVi的本体坐标系下的角速度和速度。而在AUVi的状态中，我们用到的则是欧拉角构成的旋转矩阵。因此，我们需要将本体系的角速度转换为欧拉角的微分。这种转换可以通过式（9-108）得到［26］：

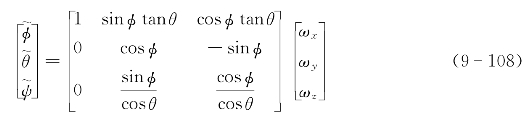
其中，ψ为偏航角；θ为俯仰角；φ为横滚角；ωx为本体系绕X轴的角速度；ωy为本体系绕Y轴的角速度；ωz为本体系绕Z轴的角速度。

根据图9-10可知，k1、k3、k5与位置控制有关，而k2、k4、k6与角度控制有关。先进行初步的仿真，考察不同控制参数对控制效果的影响。设定领航AUV进行直线运动，领航者AUV的初始位置为［0，0，0］T，速度全程保持为［2，0，0］T，初始欧拉角为［0，0，0］T，跟随者AUV的数量为1，初始位置为［－5，－5，－3］T，初始速度为［0，0，0］T，初始欧拉角为［0，0，0］T，期望位置为［1，－10，－1］T，控制周期为0．1 s，共仿真500步（50 s）。令k2＝k4＝k6＝1，在k1＝k3＝k5＝0．5和k1＝k3＝k5＝5两种情况下，两者协同运动轨迹如图9-10和图9-11所示。能够看到，不论参数为多少，跟随者AUV均能够经过一定的调整后稳定在预设的位置，并与领航者AUV的运动保持同步。此外，能够定性地看出，当k1、k3、k5越大，则位置调整的速度越快，调整过程中的曲率明显增大。本书这里所提供的数据图表详细表明了误差和速度随时间的变化过程。

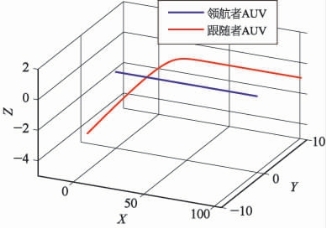
图9-10　k1＝k3＝k5＝0．5时的仿真结果

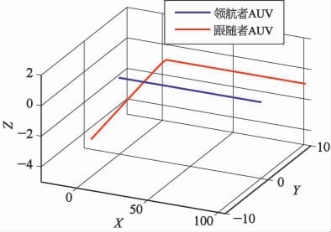
图9-11　k1＝k3＝k5＝5时的仿真结果

在k1＝k3＝k5＝0．5和k1＝k3＝k5＝5两种情况下，跟随者AUV在体坐标系下的速度曲线如图9-12和图9-13所示。

从图9-12和图9-13中可以看到，k1、k3、k5越大，速度变化率明显增大。以Y轴方向上的速度为例，当k1＝k3＝k5＝0．5时，Y轴方向上的速度控制输入量从7．5 m／s逐渐减小直到0，而当k1＝k3＝k5＝5时，Y轴方向上的初始速度控制输入量从75 m／s开始，在1 s内减小到0，平均加速度大于7 G。显然，即使是目前最先进的无人水下航行器，也无法做出如此剧烈的机动，因此，在本书建立的模型的基础上所设计的控制器，在实际使用中需要考虑航行器的实际运动控制能力，对参数和输出进行限制，避免输出不合理的控制量。

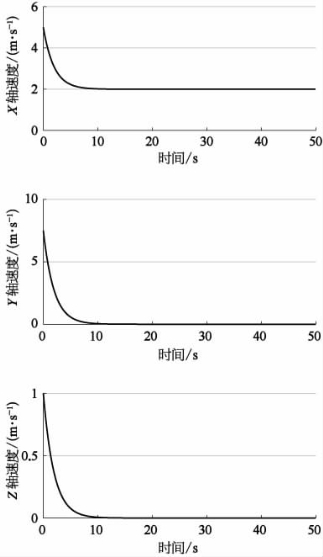
图9-12　k1＝k3＝k5＝0．5跟随者速度曲线

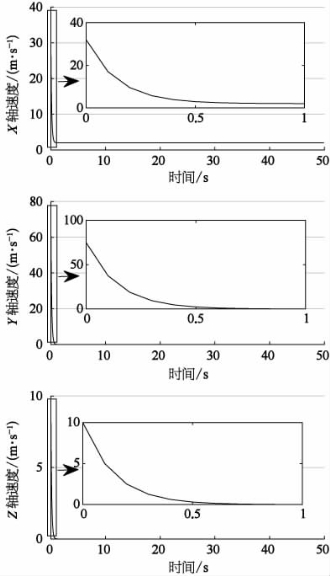
图9-13　k1＝k3＝k5＝5跟随者速度曲线

在k1＝k3＝k5＝0．5和k1＝k3＝k5＝5两种情况下，跟随者AUV在惯性坐标系下三个方向上的误差曲线如图9-14和图9-15所示。

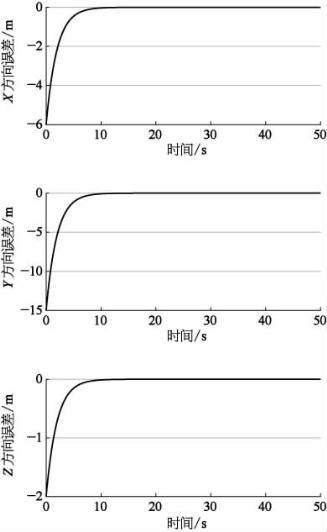
图9-14　k1＝k3＝k5＝0．5时跟随者编队误差

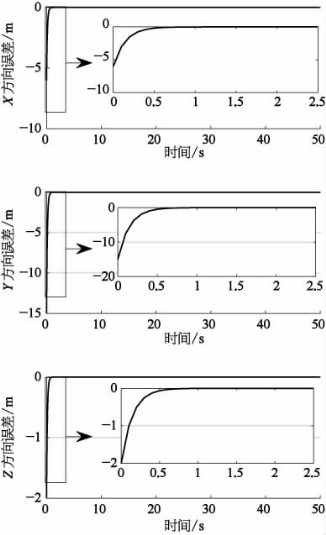
图9-15　k1＝k3＝k5＝5时跟随者编队误差

对误差的分析进一步支撑了我们的上述分析，即参数k1、k3、k5越大，误差的收敛速度越快。由于我们在进行控制器设计时已经保证了其稳定性也从另一个侧面证明了所设计的控制器在位置控制方面优良的稳定性。

接下来考察不同参数对于角度控制效果的影响。设定领航AUV进行直线运动，领航者AUV的初始位置为［0，0，0］T，速度全程保持为［2，0，0］T，初始欧拉角为［π／4，0，0］T，跟随者AUV的数量为1，初始位置为［1，－10，－1］T，初始速度为［0，0，0］T，初始欧拉角为［－π／4，0，0］T，期望位置为［1，－10，－1］T，控制周期为0．1 s，共仿真100步（10 s）。令k1＝k3＝k5＝0．5，在k2＝k4＝k6＝0．5和k2＝k4＝k6＝5两种情况下，两者协同运动轨迹如图9-16和图9-17所示。其中，附在红色跟随者AUV轨迹上的洋红色箭头为跟随者AUV在此位置时的艏向。能够看到不论参数为0．5还是5，跟随者AUV的艏向角度都能够随着时间收敛到与领航者AUV一致。此外，还能够直观地看出参数越大，则角度调整的速度越快，越能尽快收敛到目标值附近，调整过程中的角加速度越大。

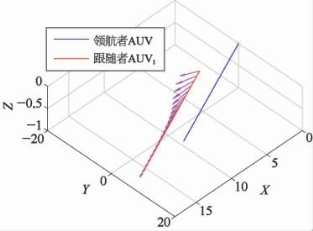
图9-16　k2＝k4＝k6＝0．5时的仿真结果

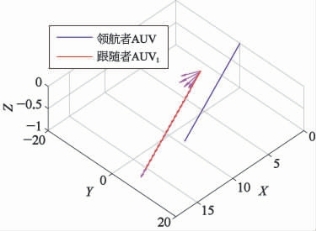
图9-17　k2＝k4＝k6＝5时的仿真结果

在k2＝k4＝k6＝0．5和k2＝k4＝k6＝5两种情况下，跟随者AUV绕Z轴的转向率如图9-18和图9-19所示。(www.daowen.com)

从图9-18和图9-19中能够看到，与位置控制类似，参数越大，调整时的转向率越大。当k2＝k4＝k6＝5时，控制器输出的转向率从286．5°／s增加到最高341．2°／s，并在1 s内减小到0。角加速度超过5．82 rad／s，这同样是不现实的。因此，在角度控制方面也必须增加参数和输出的限制，使之保持在AUV运动控制的合理范围内。

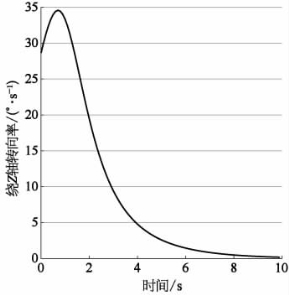
图9-18　k2＝k4＝k6＝0．5时绕Z轴转向率

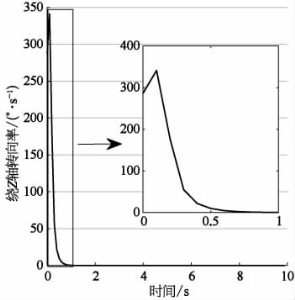
图9-19　k2＝k4＝k6＝5时绕Z轴转向率

在k2＝k4＝k6＝0．5和k2＝k4＝k6＝5两种情况下，跟随者AUV与领航者AUV的偏航角误差如图9-20和图9-21所示。

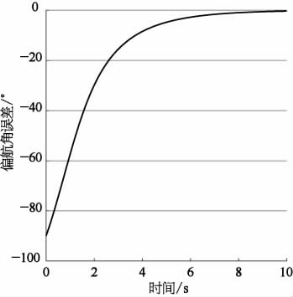
图9-20　k2＝k4＝k6＝0．5时的偏航角误差

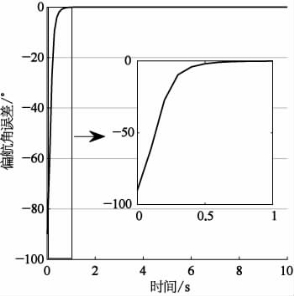
图9-21　k2＝k4＝k6＝5时的偏航角误差

对偏航角误差的分析进一步支持了上述结论，即参数越大，欧拉角的误差收敛越快。并且，由于在控制器设计之初即通过李雅普诺夫函数导数的负定保证了其稳定性，因此可以看到控制器始终保持着稳定。

此外，在仿真中还发现，控制器增益参数k不能随意取得过大。虽然在通过李雅普诺夫直接法构造控制器时，保证了控制器在所设计的协同运动模型下的稳定性，但是由于使用的是连续系统进行的分析，在实际仿真时则将其离散化处理。由于离散化的过程影响了步长，因此对系统的稳定性有所影响。这实际上是由于参数与控制频率配合不当导致的。经过试验，当控制频率与最大参数处于同一数量级时，就可以避免因为离散化出现的不稳定现象。

综合以上分析，为了避免控制器的不合理输出和系统出现不稳定，控制器增益参数k的取值不宜随意地取较大的值，并且k的数量级与控制频率应当一致。

最后进行多个跟随者AUV的协同运动仿真试验。设定领航者AUV的初始位置为［0，0，0］T，速度全程保持为［2，0，0］T，初始欧拉角为［0，0，0］T，初始角速度为［0，0，0］T，角速度绕本体坐标系Z轴做正弦转动，转动的幅度为1、频率为1／40 Hz；同时绕本体坐标系Y轴做正弦转动，转动的幅度为1／60、频率为1／20 Hz。

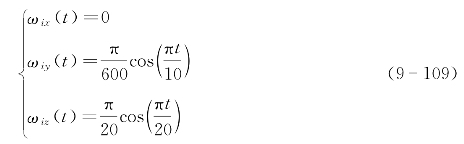
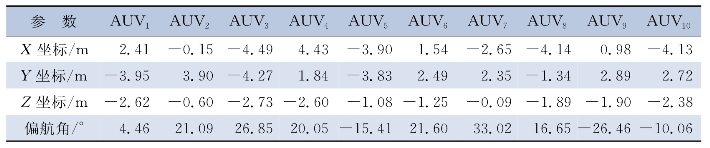
设定10个跟随者，在领航者周边随机生成跟随者AUV的初始位置和初始航向角，其他欧拉角设为0，初始位置和初始航向角见表9-1。

表9-1　随机生成的跟随者AUV初始位置和初始航向角

设定协同运动预期位置满足式（9-110）：

设定控制器的控制参数为［0．5，0．5，0．5，0．5，0．5，0．5］，控制周期为0．1 s，根据之前的分析，对控制器输出进行限幅，其中每个轴向最大速度为3 m／s，最大转向角速度为12°／s，共仿真200步（20 s），领航者和跟随者的运动轨迹如图9-22所示。

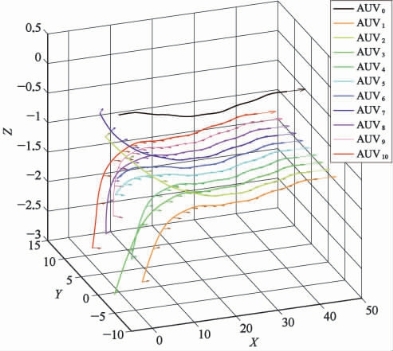
图9-22　协同运动仿真试验轨迹图

图9-22中跟随者AUV的轨迹上的箭头表示此刻该AUV的艏向。从图中能够看出，各个跟随者AUV从各自的随机起始位置和起始欧拉角向领航者AUV靠拢。在此过程中，跟随者AUV逐渐在控制律的作用下变换为设定的队形。此后，随着领航者AUV的运动趋势，跟随者AUV也进行相同的运动。不失一般性地，取AUV5进行编队误差分析，如图9-23和图9-24所示。

从图9-23、图9-24中能够看出，跟随者AUV5位置和欧拉角误差均在10 s内消除到接近0，并且在之后的运动中能够稳定地跟踪领航者，体现为误差在0周围波动，而不会再次增加。

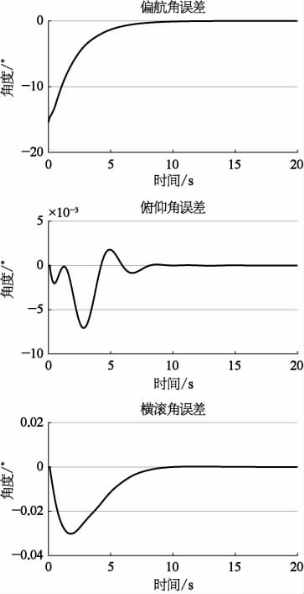
图9-23　AUV5协同运动欧拉角误差曲线

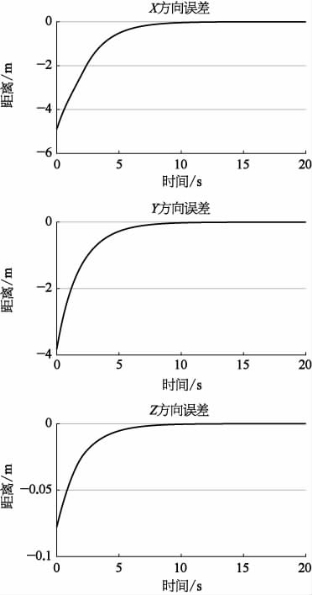
图9-24　AUV5协同运动位置误差曲线