摄像机作为视觉伺服控制研究的基础，一个精确的摄像机模型显得尤为必要，摄像机的性能也直接关系着视觉伺服控制的效果。不同的摄像机模型适应于不同的应用环境，本书研究内容建立在经典的针孔模型的基础上，在本章将针对针孔模型做详细介绍。

（1）针孔模型。

对于摄像机的模型而言，最简单而有用的模型就是针孔模型［1］，针孔可以想象成墙上的小洞，光线只能从小洞射入，处理时可以根据几何原理中的投影射线来分析，如图8-1所示。

图8-1　针孔摄像机模型

右图存在如下关系：

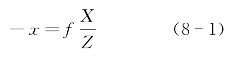
其中，f为摄像机焦距；Z是摄像机到目标物的距离；X为目标物的长度；x是目标物在图像平面中的长度。

将针孔模型转换为等效模型可简化运算，简化等效模型如图8-2所示。

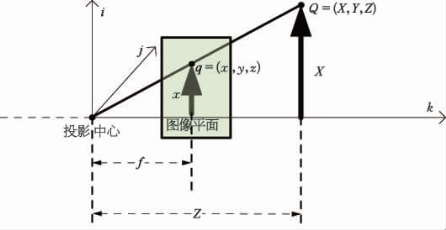
图8-2　针孔摄像机等效模型

等效模型的成像关系表示为：

（2）内参模型。(www.daowen.com)

摄像机的针孔模型是理想化的线性模型，这种模型忽略了透镜所产生的畸变。针孔模型下图像坐标系如图8-3所示，O0为光轴中心，O1为摄像机成像仪的中心。

由于安装精度问题，导致摄像机成像仪中心不在光轴上，所以需要新引进两个参数，即x轴与y轴方向上的偏差cx和cy，这样我们可以得到摄像机模型为：

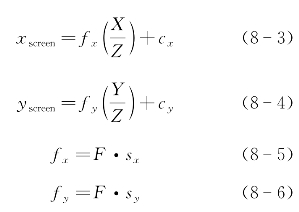
其中，点（xscreen，yscreen）为投影点；Q＝（X，Y，Z）为目标物在世界坐标系下的点；q＝（x，y，f）为点Q在图像内的投影点；fx为x方向上的焦距；fy为y方向上的焦距。

由于F为透镜的物理焦距长度（mm），（sx，sy）表示成像仪上每个像素单元的尺寸（像素／mm），则根据式（8-5）、式（8-6）可知fx和fy的单位为像素。

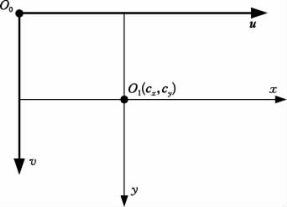
图8-3　图像坐标系

投影变换表示目标物上Q的物理点坐标（Xi，Yi，Zi），映射到投影平面，获得映射点q＝（xi，yi）的变换过程。

通过齐次坐标将q＝（xi，yi）转换为q＝（q1，q2，q3）的形式，将摄像机的内参看作一个3×3矩阵，即为摄像机的内部参数矩阵，目标物上的点投影到摄像机图像平面的过程就可以描述为：

其中，。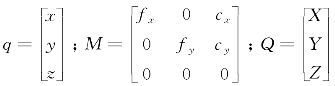

代入式（8-7）展开后可得：

其中，cx、cy、fx、fy为摄像机的内参数，在得到这些参数后，即可获得目标在图像中的位置与实际位置之间的关系。为了获得摄像机内参数，需要对摄像机进行标定。