滚动时域优化估计问题可以被看作为一个非线性最小二乘问题。在仿真计算中，MATLAB求解问题时是利用非线性优化工具箱。但是在真实系统的解算中，需要用计算机语言编程来求解方程组，实现优化估计计算。那么可以将系数矩阵转换为一些特殊的结构，简化计算，可以达到降低计算复杂度的效果。

为方便分析，先以无约束非线性优化估计问题为例，非线性系统方程为：

在每一个迭代步长j中，通过：

更新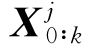，使目标函数φk满足：

其中，在每一个迭代步长中，将f（·）和H（·）进行线性化：

其中，

那么，无约束优化估计问题7．1在每一个迭代步长j里通过线性化转变为线性最小二乘优化：

其中，

利用对称正定矩阵性质将上面的问题写成矩阵形式：

其中，对矩阵进行分块：

那么问题7．3的优化问题的优化解转变为如下线性方程的解：

对线性方程（7-6）中的系数进行详细分析如下：

将A T A中分块矩阵的具体元素代入：

其中，(www.daowen.com)

另一方面，线性方程（7-49）的等号右边：

通过观察式（7-50），可以发现A T A是带状对角矩阵结构，那么方程（7-6）就可以采用LU分解和向前替换及回代的方法来高效率地计算求解：

由式（7-51）的第一个方程先解出中间变量y，在回代其第二个方程解出线性方程的解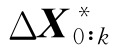，即得到优化估计问题的最优化解。

在实际应用中，系统往往是约束非线性系统。针对考虑带约束条件（7-46）的非线性优化估计问题，基于上文所述的无约束非线性优化估计问题，类似式（7-52），对带约束非线性估计问题目标函数线性化后可得：

约束条件表达式可以改写为：

其中，

一般应用原始对偶内点法来求解带约束优化估计问题。约束条件表达式（7-20）的拉格朗日函数表示为：

其中，λ是拉格朗日算子矢量。

由于约束条件包含等式和不等式，利用式（7-4）和式（7-5）的矩阵分块，带约束非线性优化估计问题的KKT条件用下式给出：

在原始对偶内点法中，可以利用牛顿方程来解决KKT条件。假设递推过程中当前点和迭代步长分别是（ΔX0∶k，λ）和（δX0∶k，δλ），因此式（7-14）的牛顿迭代的每一步用下式表示：

对式（7-15）利用矩阵舒尔补，δX0∶k的系数表示为：

根据式（7-13），有d－GΔX0∶k≥0。由KKT条件可以得知λ≥0，且矩阵分块R是正定的，所以也是正定的。那么通过比较上述约束优化估计问题系数矩阵AδX0∶k和本节第一部分无约束优化估计问题系数矩阵（7-4），两者矩阵形式结构相同，因此也同式（7-8）形式相同，是带状对角矩阵，可以利用矩阵LU分解求解优化估计问题，提高求解效率。

若是利用费舍尔信息矩阵的观点分析式（7-16），式（7-57）中的表示约束条件的部分G T（diag（d－GΔX0∶k））－1 diag（λ）G，可以认为这些约束被当成从一个虚拟传感器获得的额外量测信息来求解优化估计问题，因此估计结果更加精确，符合实际情况。