时域窗口长度N是滚动时域估计的一个重要的可调参数，它的大小直接影响到MHE算法的估计精度和计算时间。使用配置为Inter（R）Core（TM）2 T6600＠2．2 GHz CPU、4 GB内存的电脑运行MATLAB2012a进行仿真。在仿真计算中，N分别取5、10、20、50，比较EKF-MHE算法和UKF-MHE算法的计算时间。定位误差利用蒙特卡洛法重复计算50次，比较两种算法的平均估计精度。其他仿真初始条件相同。

表7-1列出了不同滚动窗口时域长度下EKF-MHE和UKF-MHE的平均估计精度。表7-2列出了不同时域长度下EKF-MHE和UKF-MHE算法的计算时间比，其计算基准为N＝5时EKF-MHE的计算时间。通过对比分析可以看出，随着滚动时域窗口长度N的增加，优化估计时考虑的过去的信息越多，算法估计结果越来越精确，但是计算所耗费的时间越长。在相同窗口长度下，UKF-MHE的估计精度略优于EKFMHE的估计精度，计算时间大部分长于EKF-MHE，但是不能确定的说UKF-MHE算法计算速度一定低于EKF-MHE算法。

表7-1　不同滚动窗口时域长度下EKF-MHE和UKF-MHE的平均估计精度

表7-2　不同滚动窗口时域长度下EKF-MHE和UKF-MHE的计算时间比(www.daowen.com)

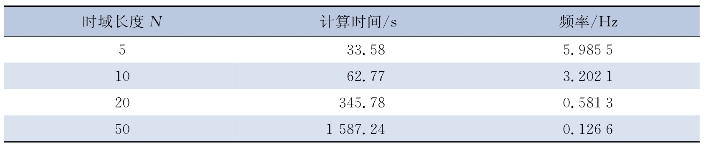
表7-3列出了不同时域长度下EKF-MHE算法的计算时间，其中频率是以计算时间内AUV状态更新的次数201次计算的。当算法的状态更新频率要大于量测信息获取的频率时，算法能够较好地利用量测信息对位置状态进行修正，满足实时估计的要求。获取量测信息的频率是0．1 Hz。对比表7-3，可以看出各个时域长度对应的频率都大于0．1 Hz，但是当N＝50时，计算时间过长，且频率只是略高于状态更新频率，不适合应用于实际情况。当时域长度N不超过20时，算法可以较好地满足实时在线估计的要求。

表7-3　不同时域长度下EKF-MHE算法的计算时间

综上所述，基于EKF、UKF近似到达代价的滚动时域估计算法能够应用于实时在线估计中。在实际情况中，对滚动时域窗口长度N的选择，需要综合考虑对估计精度和实时估计中计算时间的要求。上述对算法的计算时间分析全部采用的是MATLAB实时仿真分析，若采用类似C＋＋等编译语言，或者性能更高的计算芯片的出现，那么在真正的实际应用中，滚动时域估计算法的计算速度会得到进一步提升，更好地应用于实时在线估计问题。