前叙述的EKF-MHE协同定位算法在多AUV协同定位的应用中具有较高的计算效率，但是由于利用了EKF算法对非线性部分线性化的方法近似求得到达代价函数，这会造成状态估计精度的下降。特别是当非线性系统中量测方程的泰勒展开式中的高阶项不能忽略时，会导致比较大的误差。此外，若系统中雅克比矩阵推导过于复杂，也会导致EKF失效。因此，本节将利用无迹卡尔曼滤波进行到达代价函数的计算，将EKF中统计特性传播方式的线性化近似用Unscented变换方法代替，研究UKF-MHE协同定位算法，降低线性化损失。

基于前文描述，可先利用UT变换求取k时刻对AUV的位置估计预测和误差的协方差矩阵的一步预测Pk＋1，k。对其对应的σ点集，当存在界限时，其分布应该在可行域内。假设表示σ点的趋势方向，stepk，i表示σ点在这些方向上的步长。那么在UKF中，，这表示UKF所选σ点对于当前状态估计呈对称分布。这时，需要考虑有无约束的两种情况：

第一种情况，约束不起作用时，MHE算法通过上述UKF方法求取σ点集；

第二种情况，当约束起作用时，在计算近似到达代价函数时，需要考虑约束条件。那么，第一种情况中的σ点集的选择是不合适的。这时，取σ点的步长为：

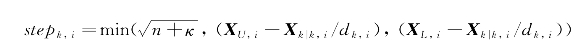
其中，XU，i和XL，i分别表示约束在σ点集在dk，i方向上的上界和下界；Xk｜k，0表示中心点，其含义与UKF中定义相同。

由于存在约束条件，σ点集对于中心点，也就是当前状态估计，不是呈对称分布的，但是这样选择更加符合状态的约束条件。

带约束的权系数计算参考Vachhani对于不同目标的权系数计算推导，考虑到：

对σ点的权系数进行如下计算：

其中，

求取权系数后，按照式（7-31）计算σ点ξk｜k，i。

通过系统状态方程（7-1）传播，计算得到状态预测采样点：(www.daowen.com)

利用ξk＋1，i和ωi计算位置估计预测和误差的协方差矩阵的一步预测Pk＋1，k：

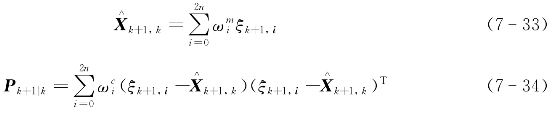
利用一步预测结果，通过量测方程（7-10）传播，计算量测预测采样点γk＋1，i：

对计算对量测的一步预测：

在获得最新的量测量Zk＋1之后，计算滤波增益矩阵K，并对状态和协方差阵进行更新：

UKF进行之后利用得到的协方差阵更新Pk＋1｜k＋1，再根据式（7-27）计算近似到达代价函数，同EKF-MHE算法相似，进而按照7．3小节中问题7．3给出的MHE计算步骤进行多AUV协同定位的状态估计，但是却避免了系统状态方程和量测方程的线性化。

对所设计的算法进行仿真验证，为便于对UKF-MHE算法和EKF-MHE算法进行比较，仿真初始条件与前文中相同。

如图7-10所示，利用EKF-MHE与UKF-MHE协同定位算法得到的AUV航行轨迹同理想轨迹偏差较小，基本吻合。UKF-MHE算法估计的轨迹较EKF-MHE算法估计的轨迹更加平滑，接近理想轨迹。UKF-MHE算法定位精度高于EKF-MHE，其定位误差基本被限定在1 m以内。这是由于UKF算法利用UT变换处理系统非线性特性，排除了EKF算法中线性化的误差，提高了估计精度。

图7-10　利用EKF-MHE与UKF-MHE协同定位算法得到的AUV航行轨迹