基于EKF近似到达代价的滚动时域估计协同定位算法分为两步：第一步是航位推算，它预测了从AUV的位置并且运用EKF算法来对其姿态进行更新；第二步是运用MHE算法来对有限时域内的量测数据以及约束条件加以考虑后进行位置估计误差的优化。

假设系统初始位置状态的先验估计为初始协方差阵为P0，系统噪声协方差阵为Qk，量测噪声协方差阵为R，且三者均可逆。那么，设定滚动时域窗口长度N，根据式（7-5）计算近似到达代价函数ΘT（X）中的协方差矩阵，进而按照7．3小节中问题7．3给出的MHE计算步骤求解进行多AUV协同定位的状态估计。

利用MATLAB对上一小节所设计算法进行数值实例仿真，以检验算法的可行性与实用性。在数值实例仿真中，主、从AUV航行轨迹如图7-4所示。主AUV（图中AUV1）从起点（0 m，0 m）出发，以航速2．5 m／s、航向角22．5°沿直线匀速航行，每间隔500 s进行一次转向机动。从AUV（图中AUV2）从起点（0 m，100 m）出发，以航速2 m／s沿与X轴平行的直线匀速航行。从AUV上装备低精度IMU获取速度信息和航向角信息，测量噪声分别取的零均值高斯白噪声，并且两者独立不相关。根据量测方程，引入量测噪声为均为水平距离的平方，二者独立不相关。考虑到水声传播速度低以及水下环境的复杂性，OWTT方式获得的量测信息频率设为0．1 Hz。MHE算法中滚动时域窗口长度N＝5。规定从AUV任务执行区域范围为宽度为10 m的海底区域，对协同定位系统引入约束条件，即仿真中对从AUV的在Y方向的航行范围限定为±5 m。定位误差的计算采用蒙特卡洛法，重复仿真计算100次，取统计平均值。

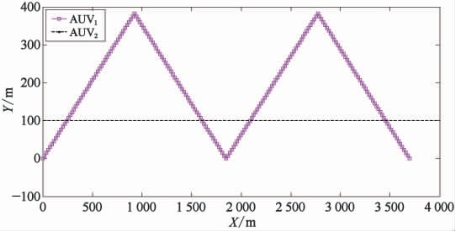
图7-4　主、从AUV航行路线

AUV2分别使用DR，EKF和EKF-MHE协同定位算法进行定位，其航行轨迹由图7-5所示。AUV2使用航位推算算法进行定位的轨迹随着时间推移逐渐偏离真实轨迹，而EKF和EKF-MHE协同定位算法下的轨迹同真实轨迹偏差较小，基本吻合，达到比较好的定位效果。当从AUV只依赖内部传感器进行航位推算导航时，其定位误差是随着时间推移不断增大并最终发散，导致定位失败；当引入水声测距所获得的量测信息并利用EKF和EKF-MHE算法设计的协同定位算法对定位结果进行修正后，导航定位误差显著减小。

图7-5　AUV2协同定位算法仿真轨迹

EKF和EKF-MHE两种算法对应的航行轨迹以及图7-6、图7-7中EKF和EKF-MHE两种算法的定位误差加以比较可以发现，EKF算法的估计结果在航行某些阶段中超出了预设的任务限定区域Δy≤±5 m，若限定区域为河道或者海底峡谷，EKF的定位结果是不符合实际情况的。而EKF-MHE算法定位误差较单独使用EKF进行协同定位要小，定位精度更高，其估计的航行轨迹没有超过预设的任务限制区域，符合实际情况。这是由于MHE算法较EKF算法可以更好地处理系统非线性特性，同时能够引入实际系统中存在的约束，并且有限度地考虑了过去的有效信息，达到了更好的估计效果。(www.daowen.com)

图7-6　协同定位算法与航位推算定位误差比较

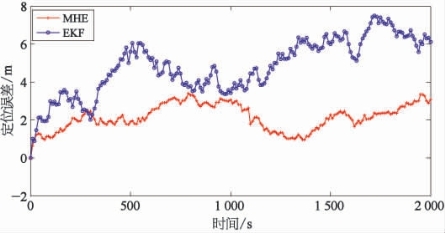
图7-7　协同定位算法定位误差

在实际航行中，由于水下环境复杂，整个多AUV协同系统以及AUV之间通过水声测距所获得的量测信息都有可能遇到突发的干扰，这可能会造成短时间内协同定位的误差急剧增大甚至是定位失败。在仿真实验中，初始条件与本节前述仿真相同。假设在航行过程中，AUV1和AUV2之间的水声测距突然受到噪声干扰，如图7-8、图7-9所示，从AUV基于内部传感器的航位推算系统没有受到干扰，但是随时间累积的误差导致定位结果逐渐偏离。相比于基于EKF算法进行协同定位，基于MHE算法进行协同定位的AUV的航行轨迹基本没有受到影响，具有很强的鲁棒性。这是因为EKF算法在进行估计时仅使用当前时刻所获得的量测信息，而MHE算法能够利用系统的约束条件来防止估计结果偏离，并在位置估计中充分考虑AUV过去和当前的位置信息，得到更好的估计效果。

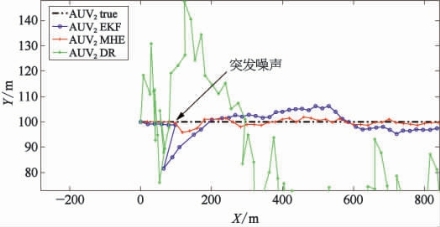
图7-8　噪声干扰下协同定位算法轨迹

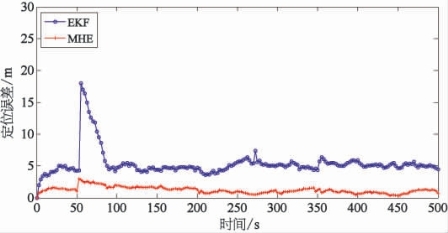
图7-9　噪声干扰下协同定位算法定位误差