到达代价是指系统在满足约束条件的情况下从初始状态X0到达给定状态z所需要付出的代价。到达代价函数是滚动时域估计中一个基本的概念，它提供了一种融缩量测数据的方法，表达了固定时域外的其余测量数据对当前时刻估计的影响，在全信息估计问题与固定时域估计问题之间建立了联系，将无限维数全信息估计问题7．1等价转变为有限维数的滚动时域估计问题7．2，从而保证了求解问题的可行性。

对于约束系统而言，一般来说，到达代价函数很难直接得到其表达式，但是二次型无约束线性系统往往可以求得解析表达式。因此，往往采用无约束线性系统到达代价函数近似地替代有约束系统的到达代价函数。

基于上一小节的推导，对优化估计问题7．2中系统模型采用线性系统模型（7-14），那么对于无约束线性系统，MHE的优化估计问题7．2可以简化为：

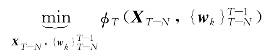
其中，

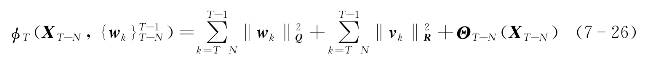
根据滚动时域估计的基本原理我们将基于最新的一个测量数据重复求解上述优化问题，得到状态估计值。当满足P＝P0，并且采用卡尔曼滤波的协方差更新，目标函数中的到达代价由前一时刻得到，到达代价函数可以表示为：

其中，表示T－N时刻的最优到达代价函数，PT－N满足KF的协方差更新：

若取N＝1，基于上一小节的推导，此时无约束线性优化估计问题同卡尔曼滤波等价。令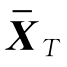是对T时刻起始状态XT的先验估计，取其等于前一个时刻的状态估计值，即：

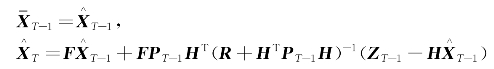
当系统为非线性且存在约束条件时，在非线性约束系统到达代价函数无法计算的时候下，我们希望近似的到达代价函数尽可能准确地表示滚动时域外过去的数据对估计的影响。利用近似表示到达代价［2］。

因此，约束优化估计问题7．2变为如下问题：(www.daowen.com)

问题7．3

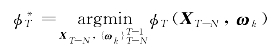
满足系统（7-7）、（7-8）和时域约束条件（7-9）；

其中目标函数为：

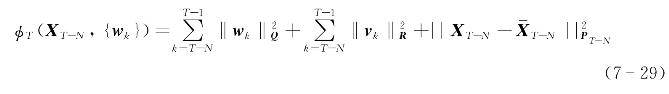
当系统为非线性系统或者系统存在约束条件，一般很难求得到达代价的解析表达式。因此，如上述问题7．3可以采用无约束线性系统的到达代价函数近似地代替有约束系统的到达代价函数。近似到达代价函数可以通过将系统模型围绕估计状态轨迹泰勒展开，也就是利用EKF协方差更新近似到达代价函数［3］；也可以将EKF中统计特性传播方式的线性化近似用UT变换方法代替，即利用UKF协方差更新近似到达代价函数。因此，给出滚动时域估计算法的计算步骤和流程图如下：

①给定Q、R，初始位置状态的先验估计和P0以及滚动时域窗口长度N；设定T＝1。

②当T≤N时，求解带有约束的全信息优化问题7．1，得优化解为并由系统模型（7-7）计算出当前时刻状态的估计值。

③当T＞N时，求解带有约束的有限时域优化问题7．3，得到优化解并由系统模型（7-7）计算出当前时刻状态的估计值。

④根据需要，选择UKF或者EKF协方差更新计算下一时刻的误差协方差矩阵PT－N＋1，并用系统模型（7-7）或EKF和UKF中一步预测方程计算下一时刻的先验估计状态。

⑤在下一时刻，用最新的量测值ZT构造新的量测数据集，定义T＝T＋1返回第②步。

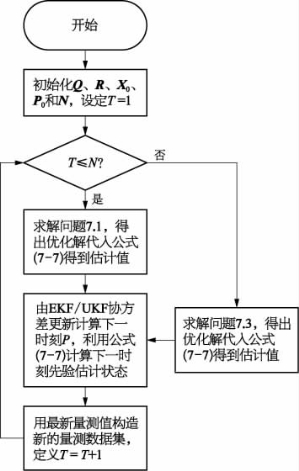
图7-2　滚动时域估计算法流程图