状态估计问题可以描述为：给定T时刻之前的所有量测集Z1∶T－1＝｛Zk，k＝1，…，T－1｝及其概率分布，寻找系统状态｛X0，X1，…，XT｝的概率分布，以获得最大可能的估计状态其中表示在T－1时刻对k时刻的状态估计，即保证条件概率密度函数：

达到最大。

记LT（·）为式（7-1）的条件概率密度函数，则状态估计问题可表示为：

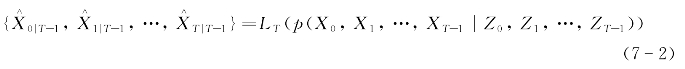
通常情况下，函数LT（·）可选择为后验贝叶斯估计的最大值或期望，即：

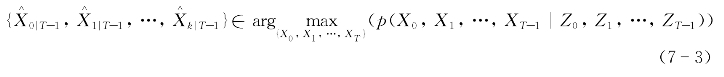
考虑非线性随机滤波系统（7-2），假设Xk＝fk（Xk－1，uk－1，ωk－1）＝fk（Xk－1，uk－1）＋ωk－1，Zk＝Hk（Xk，υk）＝Hk Xk＋υk，ωk为系统噪声，υk为量测噪声，系统噪声与量测噪声相互独立。依据马尔科夫性质和对数性质，式（7-3）可以转变成

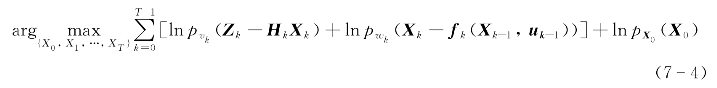
如果初始状态X0的先验估计服从；系统噪声ωk服从ωk～N（0，Q 2），量测噪声υk服从υk～N（0，R 2），则：

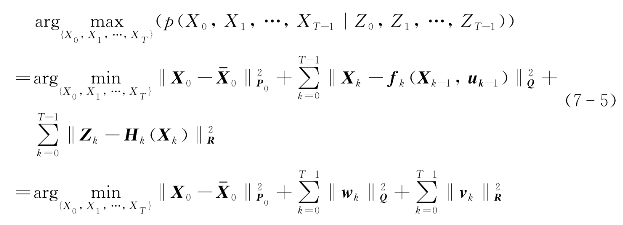
其中，。

因此，如果系统初始状态X0的先验估计状态服从则在T时刻由式（7-3）所描述的状态估计问题等价于下面的约束优化估计问题。

问题7．1

满足系统：

和时域约束条件：

其中目标函数为：

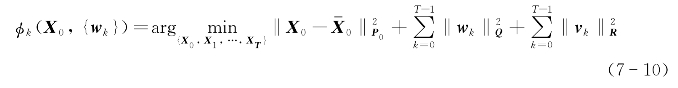(www.daowen.com)

其中，Χk，Wk，Vk通常选择为有限维数的多面体凸集；Xk和Zk分别为系统状态和量测输出；ωk为系统噪声，υk为量测噪声，服从均值为零，协方差分别为Q，R的正态分布，且相互独立。

从统计学意义上进行解释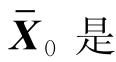：系统初始状态X0的一个先验估计，矩阵P0反映了对这个先验估计的信心。如果P0大，则最小化的结果将使X0更加接近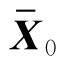，这表示设计者认为先验估计值可靠。如果P0取零，那么则该项对目标函数的贡献为零，也就是说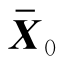将不会影响求解，表示设计者认为先验估计值不可信，从而不予采纳。矩阵Q反映了对系统模型精度的信心，而矩阵R反映了对传感器量测结果的信心。因此，如果Q＞R，那么对传感器量测精度的信心要强于系统模型的信心，反之则表示对系统模型精度更有信心。

求解问题7．1主要是通过极小化目标函数φk（X0，｛wk｝）得到优化解，记为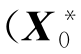，即系统初始状态和系统噪声，将优化解代入系统方程（7-7），则可以求得k时刻下系统状态的估计值。在下一时刻，将最新量测值推入量测数据序列，根据模型预测控制的滚动优化原理，令T＝T＋1，重新求解约束估计问题7．1。

问题7．1利用了全部的量测数据来估计系统状态和系统噪声，故称之为全信息滚动时域估计（full information estimation，FIE）。显然，随着时间的增大，问题7．1处理的数据越来越多，计算负荷越来越大，尤其是存在约束（7-9）时。当时间T→∞时，就产生了所谓的“数据爆炸”问题。因此限制优化估计问题的维数是必要的。

为了在实际问题中避免“数据爆炸”问题，Rao等人提出了滚动时域的方法，即通过引入固定的数据时域N，将问题7．1中的计算时域分为两部分，即｛k∶0≤k≤T－N－1｝和｛k∶T－N≤k≤T－1｝。目标函数（7-10）可以重新表示为：

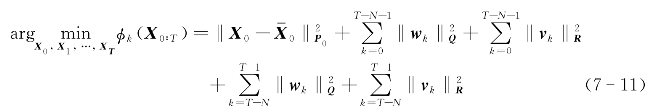
根据系统（7-7）、（7-8）的马尔可夫特性，式（7-11）的后面两项：

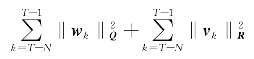
的值仅与状态XT－N、系统噪声和量测集相关。利用前向动态规划原理，可以建立起全信息估计问题与固定时域估计问题之间的等价关系，则估计问题7．1与如下问题等价。

问题7．2

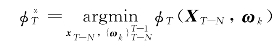
满足系统（7-7）、（7-8）和时域约束条件（7-9）；

其中目标函数为：

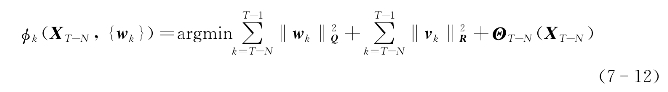
其中到达代价（arrival cost）可定义为：

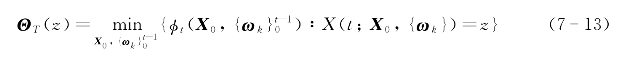
满足系统（7-7）、（7-8）和时域约束条件（7-9）。

上述估计问题中，N是滚动时域窗口长度，ΘT－N（XT－N）是到达代价，求解步骤同问题7．1。不同的是，求解问题7．2时，只利用了当前时刻前的最新的N个数据，其余量测数据对估计的影响压缩进了到达代价函数ΘT－N（XT－N）。根据滚动优化原理，在下一时刻将最新量测值推入数据序列，丢掉最旧的那个数据，维持N个量测数据不变，因此称为滚动时域估计，如图7-1所示。

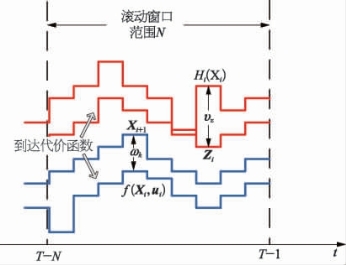
图7-1　滚动时域估计原理图

时域长度N是有限时域滚动时域估计的一个参数。如果N取值过大，求解的速度就会下降，但估计效果会随着N的增大而得到增强。所以选择时域长度N时，需要综合考虑估计精度和计算速度两个方面。通常选择N的取值为两倍于系统阶次的正整数，在实际应用需要视具体情况来进行调整。