粒子滤波作为抽样贝叶斯估计算法，随着抽样粒子数的不断增大，估计逐渐趋向状态的后验概率密度，就理论基础而言，粒子滤波算法和其他非线性滤波方法一样也是次优的滤波算法。扩展卡尔曼滤波和无迹卡尔曼滤波都依赖于高斯近似，然而实际中的很多问题都是强非线性的，状态分布往往具有多个峰值，此时的高斯近似将不能准确地表示出状态的真实分布。粒子滤波是基于蒙特卡罗采样方法和贝叶斯最优估计理论提出利用状态空间的一组加权随机样本逼近状态变量后验概率分布的滤波算法，不受模型线性程度和高斯假设的约束。

粒子滤波是指通过寻找一组在状态空间中传播的随机样本，对概率密度函数进行近似，以样本均值代替积分运算，从而获得状态最小方差估计的过程。基本粒子滤波器包括样本重要性采样和再采样，结合贝叶斯滤波体系的时间更新和观测更新两步骤进行。针对平稳的动态时变系统，假定k－1时刻系统的后验概率密度为p（xk－1｜zk－1），依据一定原则选取n个随机样本点，k时刻获得量测信息后，经过状态更新和时间更新过程，n个粒子的后验概率密度近似为p（xk｜zk），随着了粒子数目的增加，粒子的概率密度函数就逐渐逼近状态的概率密度函数，粒子滤波就达到了最优贝叶斯估计的效果。

在实际应用中，随着时间的增加，重要性权值很可能集中到少数的粒子上，从而产生粒子匮乏现象，为了降低影响，最有效的方法是选择重要性函数和采用重采样方法而不是持续增加采样粒子数。选择重要性函数方面，工程上大都采用了次优的p（xk｜xk－1）作为重要性函数；重采样方法方面，根据粒子和相应权表示的概率密度函数进行重新采样，减少权值小的粒子数，增加权值大的粒子数，最常用的重抽样方法是随机抽样方法，重采样过程增加了计算量、降低了鲁棒性、降低了粒子数的匮乏。

重要性函数选取的最优原则就是使得重要性权重的方差最小，文献［5］证明了最优重要性函数为q（xk｜x0∶k－1，z1∶k）＝p（xk｜x0∶k－1，z1∶k），但是采用最优重要性函数需要从函数p（xk｜x0∶k－1，z1∶k）抽样并计算积分，由于p（xk｜x0∶k－1，z1∶k）是多变量的、非标准的，通常很难直接从中抽样得到粒子，常规有效的解决方法就是引入一个容易采样的已知概率密度分布，并从该概率密度上采样粒子。所以在应用的角度上，多数重要性函数都采用了次优的q（xk｜x0∶k－1，z1∶k）＝p（xk｜xk－1），由于未能利用最新的测量信息，以该函数为重要性函数进行抽样所产生的方差比后验概率q（xk｜x0∶k－1，z1∶k）产生的方差要大，但是由于工程上容易实现，因此在粒子滤波算法中得到了广泛的应用［6］。

UKF递推得到的状态分布的高斯近似均值和协方差比EKF得到的更加准确，并且可以更好地估计状态协方差，与EKF估计相比UKF可以更好地逼近后验分布［7］。EKF只能用一阶泰勒展开式进行逼近，UKF后验协方差的精度可以精确到高斯先验分布的三阶泰勒展开式。因此在粒子滤波框架下使用UKF来产生更加准确的重要性分布。

以AUV导航系统为例，该非线性系统，

状态方程为：

观测方程为：

初始化：

利用Ⅰ、Ⅱ可以获得一组sigma点集及其对应的权值：

2n＋1个sigma点集的一步预测：

系统状态量的一步预测为：

协方差矩阵为：(www.daowen.com)

将2n＋1个sigma点集带入观测方程，可以得到预测的观测量：

加权求和得到系统预测均值：

加权求和得到系统预测协方差：

增益矩阵为：

状态更新为：

协方差更新为：

估计重要性权值系数：

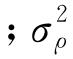其中，Z（k）为量测值；（k）为预测量测为距离量测方差。

归一化重要性权值：

根据权值，进行重抽样，复制高权值的粒子，抛弃低权值粒子，归一化重要性权值，产生新的n个粒子集：

由等权样本集得到后验均值估计、后验方差估计：

在一个滤波周期内，无迹粒子滤波同时经历了无迹卡尔曼滤波和粒子滤波过程。首先，按照UT变换中的确定采样规则获取有相应权值的样本集；然后，按照UKF算法完成对预测状态均值和方差的估计；最后，根据UKF算法得到的均值和方差进行采样并完成粒子滤波。可见，无迹粒子滤波算法不仅利用了粒子滤波对状态变量后验概率分布较好的逼近效果，也引入了UKF来产生更加准确的重要性分布，从而可以在一定程度上达到更好的估计精度。