UKF的核心思想是UT变换。UT变换理论是用固定数量的参数去近似一个高斯分布，因为这比近似任意的非线性函数或者变换更容易。具体实现原理是：在原状态分布中按照某一规则选取一些点，每个样本点都有自己的状态值和相应的加权值，使这些点的均值和方差近似等于原状态分布的数学期望和方差；将这些点映射到非线性函数中，得到相应的非线性函数值点集，并将映射的样本值加权求和得到非线性映射后点集的均值和方差。

对于任意非线性函数y＝f（x）状态向量x为n维随机变量，已知函数均值为X－和反差为P，可以通过UT变换得到2n＋1个sigma点和相应的权值来计算y的统计特征：

Ⅰ　2n＋1个sigma点：

Ⅱ　sigma点的相应权值为：

其中，下标为m的是均值权值，下标为c的是协方差权值，上标为采样点标号；λ＝a 2（n＋κ）－n是缩放比例参数，可以降低总的预测误差；α决定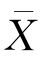周围sigma点的分布状态，调节α可以使高阶项的影响达到最小通常选取为0≤α≤1。κ为待选参数，具体取值虽然没有界限，但是通常应该确保矩阵（n＋λ）P为半正定矩阵，对于高斯分布的情况，当状态变量为单变量时κ＝2，但状态变量为多变量时κ＝3－n；待选参数β≥0是一个非负的权系数，它可以合并方程中的高阶项的动差，可以把高阶项的影响包括在内；n为状态的维数。

以AUV导航系统为例，该非线性系统，

状态方程为：

观测方程为：

其中，

由于过程噪声是隐含在系统中的，所以需要对状态变量进行扩展，可以得到增广状态变量：

初始化：

利用Ⅰ、Ⅱ可以获得一组sigma点集及其对应的权值：

2n＋1个sigma点集的一步预测：(www.daowen.com)

系统状态量的一步预测为：

协方差矩阵为：

将2n＋1个sigma点集代入观测方程，可以得到预测的观测量：

加权求和得到系统预测均值：

加权求和得到系统预测协方差：

增益矩阵为：

状态更新为：

协方差更新为：

其中，χ（i）a＝［（χ（i）x）T（χ（i）ω～）T］T。

协方差矩阵Q，R为：

无迹卡尔曼滤波不将非线性函数进行线性化，采用卡尔曼线性滤波框架，对一步预测方程使用无迹变换来处理均值和均方差的非线性传递问题，主要思路是对非线性函数的概率密度函数分布进行近似，用一系列确定样本来逼近状态的后验概率密度，而不是对非线性函数进行近似。在一个滤波周期内，无迹卡尔曼滤波利用确定的采样方法获得了一系列具有不同权值的样本，将这些样本进行映射后再利用卡尔曼滤波体系完成时间更新和量测更新。因为没有把高阶项忽略并且可以通过适当选取κ来减小系统的高阶误差，所以对于非线性分布的统计量有较高的计算精度。