【摘要】:导航系统的可观测性是指AUV在各采样时刻对系统状态量的估计能否通过AUV与信标之间的相对观测量进行解算。回避不可观测路径的方法可以在AUV运动中实时检验导航系统的可观测性,但是对于某些近似不可观测路径缺乏鉴别能力。组网AUV协同运动时,AUV间不同特性的运动路径将会对系统导航系统的可观测性产生重要的影响,为此,本节将对组网AUV的运动路径进行系统可观测性分析。
导航系统的可观测性是指AUV在各采样时刻对系统状态量的估计能否通过AUV与信标之间的相对观测量进行解算。如果导航系统不可观测,那么采用协同导航算法将无法实现对AUV位置的解算,所以导航系统的可观测性是研究AUV协同导航的关键问题之一。通常采用的方法是AUV相对信标做频繁转向机动或者回避特殊的不可观测路径来确保系统的可观测性。回避不可观测路径的方法可以在AUV运动中实时检验导航系统的可观测性,但是对于某些近似不可观测路径缺乏鉴别能力。
组网AUV协同运动时,AUV间不同特性的运动路径将会对系统导航系统的可观测性产生重要的影响,为此,本节将对组网AUV的运动路径进行系统可观测性分析。
已知某协同系统运动学模型为:
可以简写为:
观测模型为:
可求得:
利用非线性时变系统的可观测性理论,可以得出导航系统的局部可观测性矩阵为:(www.daowen.com)
其中,
因此,如果rank(Οxk)<3,导航系统将不可观测。通过分析可观测矩阵得出以下不可观测路径:
①当观测矩阵前两列成比例时,系统将不可观测。此时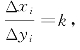 AUV以相同的速度沿着相互平行的直线路径航行,或者AUV沿着同一条直线航行;
AUV以相同的速度沿着相互平行的直线路径航行,或者AUV沿着同一条直线航行;
②当观测矩阵第一列或者第二列为零时,此时Δxi=0或者Δyi=0,AUV沿着与X轴或者Y轴平行的路径航行;
③当观测第三列为零时,Vi=0或者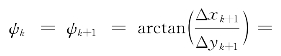
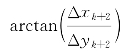 。
。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
有关自主水下航行器导航与控制技术的文章







