若要实现水下航行器的运动控制仿真研究，不管在研究过程中有无模型，都需要对AUV进行数学建模，运用模型来验证控制策略是非常有效的。AUV的模型主要可以分为两种：运动学模型与动力学模型。

正确选取坐标系，在建模过程中会起到事半功倍的效果。由于水下航行器的运动过程是非常复杂的，而且根据研究目的的不同，坐标系的选取也不尽相同，所以要建立不同的坐标系。本节主要介绍几种比较常用的坐标系：地面坐标系、体坐标系和速度坐标系，见图3-1。

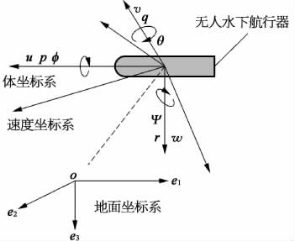
图3-1　无人水下航行器的坐标系

（1）地面坐标系。

确定重心运动，应选择与地球固连的坐标系oe1e2e3，该坐标系称为地面坐标系。坐标原点通常选在发射点或者入水点；oe1处于地平面内指向某一适当方向航行器发射方向；oe3垂直于地面并指向下方；oe2也处于地平面内垂直于e1oe3平面。按照右手法则确定坐标各轴的方向。地面坐标系描述无人水下航行器的轨迹最方便。确定重心的瞬时位置，函数e1（t）、e2（t）、e3（t）描述了重心空间运动的轨迹。

（2）体坐标系。

描述无人水下航行器的转动可选用与航行器固连的坐标系ob1b2b3，坐标系的原点取在重心处假定重心在航行器的对称轴上三个坐标轴与无人水下航行器固连。ob1在无人水下航行器的对称面内，与无人水下航行器的几何对称轴一致，指向头部；ob2处于无人水下航行器的纵对称面内垂直于ob1，指向下方，此轴称为无人水下航行器的立轴；ob3垂直于b1ob2平面，从尾部观察ob3，指向右方，此轴称为无人水下航行器的横轴。

（3）速度坐标系。

为确定作用在无人水下航行器上的流体动力，需要描述重心速度矢量V与航行器之间的相对位置，则可以选用速度坐标系来表示。速度坐标系原点取航行器重心处；u与无人水下航行器的重心轨迹的切线一致，其正方向为重心运动瞬时速度矢量V的方向，此轴称为速度轴；一般情况下，矢量V不在航行器的对称平面内。w轴在无人水下航行器的纵对称面内，且垂直于u轴，指向下方，称为升力轴；v垂直于平面u、w，称为侧力轴，侧力轴通常不在无人水下航行器升降舵平面内。

无人水下航行器作为一个刚体具有6个自由度，即无人水下航行器体坐标系在地面坐标系中的位置和体坐标系与地面坐标系之间的3个角度，即欧拉角。

（1）坐标位置。

坐标位置（x0，y0，z0）表示无人水下航行器运动时其重心在地面坐标系中的三个坐标。（x0，y0，z0）唯一确定了无人水下航行器在空间中的位置，同时也表示了无人水下航行器的水平位移、侧向位移和航行深度。

（2）欧拉角。

描述体坐标系在地面坐标系中的姿态角，有偏航角Ψ、俯仰角θ和横滚角φ。

（3）动力角。

无人水下航行器的动力角包括攻角α和侧滑角β，见图3-2。攻角和侧滑角描述了无人水下航行器运动过程中相对于水流的方位。攻角和侧滑角与速度在体坐标系中的三个速度分量之间的关系为：

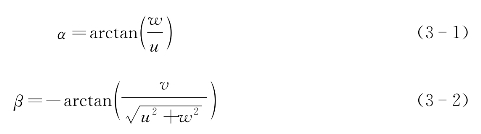
图3-2所示为攻角和侧滑角示意图。

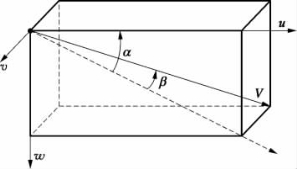
图3-2　攻角和侧滑角示意图

（4）舵角：δe、δr、δd。

δe、δr、δd分别表示无人水下航行器的升降舵角、方向舵角和差动舵角。δr若为正，当升降舵角打下舵时，δe为正。当方向舵角打右舵时（从尾部向头部看），δr为正。当升降舵左右两片舵或方向舵上下两片舵具有不同的舵角时，便构成了差动舵，两片舵的舵角值为δd。图3-3所示为水下航行器的舵配置。

从地面坐标系到体坐标系的转移矩阵可以通过三次旋转得到，旋转的顺序选为欧拉角旋转顺序：偏航角—俯仰角—横滚角。在旋转的过程中，引入两个中间参考坐标系，它们的基本向量为：（x1，x2，x3）和（y1，y2，y3）。旋转按照如下次序进行，如图3-4所示。

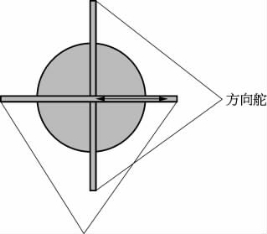
图3-3　水下航行器的舵配置

①地面坐标系E绕e3轴旋转一个偏航角Ψ，得到坐标系（x1，x2，x3）。

②坐标系（x1，x2，x3）绕x2轴旋转一个俯仰角Θ，得到坐标系（y1，y2，y3）。

③坐标系（y1，y2，y3）绕y1轴旋转一个横滚角Φ，得到坐标系B。

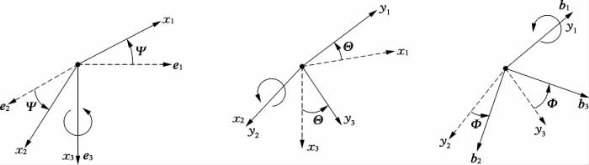
图3-4　欧拉角的旋转顺序

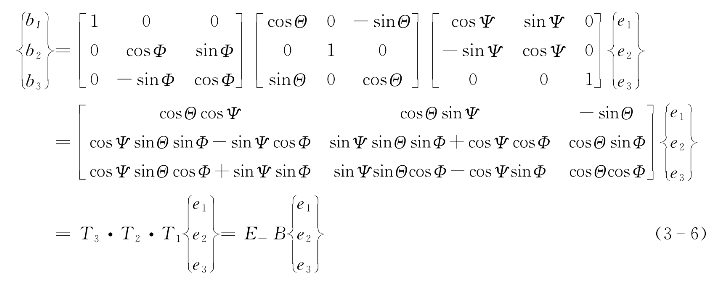
从文献［2，5］中可以得到无人水下航行器航行时受到的水动力，并且可以将水动力分解到速度坐标系，得到水动阻力和水动升力的计算公式：(www.daowen.com)

其中，Lfin为水动升力；Dfin为水动阻力；ρ为海水的密度；V为航行器的速度；Sfin为舵的粘湿面积；clfin为升力系数；cdfin为阻力系数。

因此可以得到作用在舵上的力在体坐标系下的分量：

方向舵1：

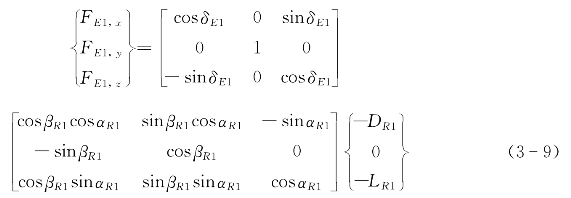
方向舵2：

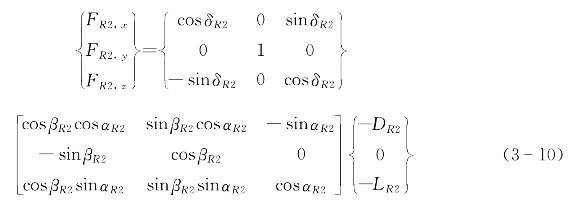
升降舵1：

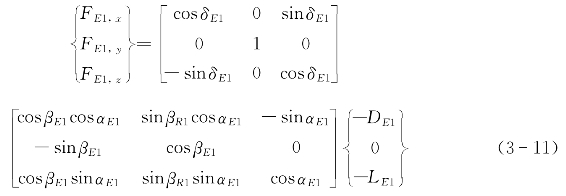
升降舵2：

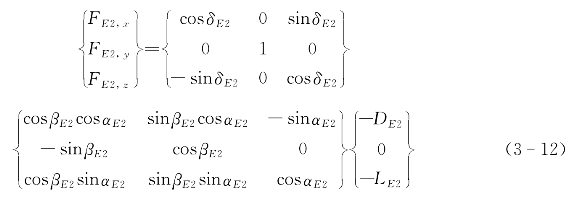
其中，δ*表示航行器的舵角；β*和α*分别表示舵的攻角和侧滑角。

式（3-9）～式（3-12）给出了作用在舵上的水动力在体坐标下的表达式。需要求出作用在舵上的水动力相对于重心CG的力矩，水动力力矩可以通过式（3-13）求取：

在这种情况下，舵是固定在无人水下航行器上，水动力的中心CP仅相对于固定点移动，因此可以得到水动力的中心CP的位置。

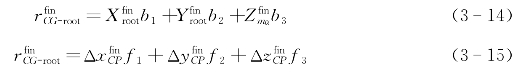
方程（3-16）～方程（3-19）给出了舵上的水动力压力中心到重心的距离：

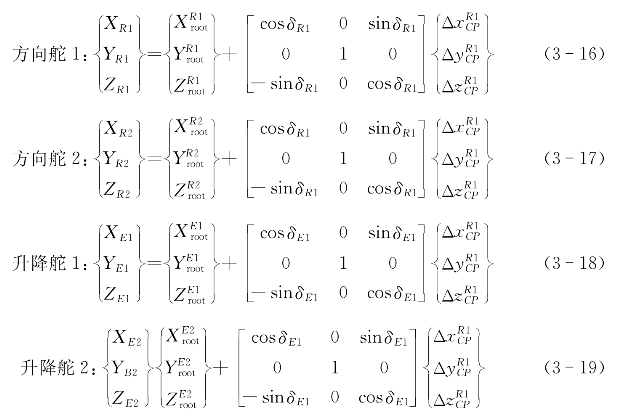
利用公式（3-20），可以得到作用在舵上的水动力相对于重心的力矩：

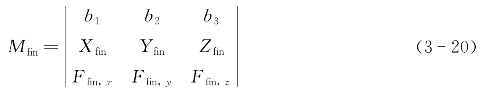
（1）AUV受到的浮力：

式中，ρ为航行器的排水体积。

浮力的方向沿着地面坐标系e2轴的反方向，其在体坐标系的各分量为：

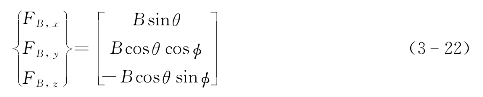
因为水下航行器的浮力通过重心，因此在体坐标系中，相对于重心不产生力矩。

（2）AUV受到的推力：

因为无人水下航行器的推力通过重心，因此在体坐标系中，相对于重心不产生力矩。

（3）无人水下航行器受到的重力：

重力的方向沿着地面坐标系e2轴的方向，其在体坐标系中的各分量为：

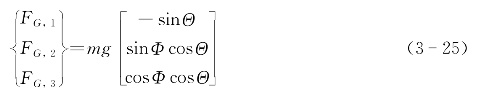
因为无人水下航行器的重力通过重心，因此在体坐标系中，相对于重心不产生力矩。