长基线定位系统在为AUV等水下航行器定位时，通常将长基线测距单元安装在AUV上，将多个声信标锚定在海床上［13］。测距单元通过周期性发送询问信号呼叫声信标，各声信标收到询问信号后回复不同的应答信号用于测距单元检测。测距单元完成对应答信号的检测后，可获得各个声信标与测距单元的声传播时间，进而求得各声信标与测距单元之间的距离，解算出载体与各个声信标之间的相对坐标。若已知各声信标的经纬度／大地坐标信息，则可以求得载体在地球上的绝对位置坐标［14］。

2．3．1．1　长基线定位基本原理

长基线定位系统具有多种解算模型，其中以球面交汇模型最为常用，其使用距离信息作为观测量，既适用于测距单元和声信标精确同步的同步工作模式，也适用于无需同步的应答工作模式［15］。本书以球面交汇解算模型为例，介绍长基线系统解算原理，图2-25为长基线定位系统工作原理的基本示意图。

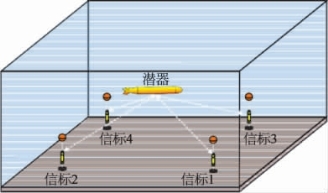
图2-25　长基线定位基本原理

设已知声信标在水下的坐标为（x，y，z），i＝1，2，3，4，测距单元的坐标为（x，y，z），假设水下声速为恒定值c，声信标i与测距单元之间的单程传播时间为ti，若不考虑声线弯曲等因素的影响，可得到声信标i与测距单元之间的距离为ri＝c·ti，i＝1，2，3，4。根据声信标和测距单元之间的几何关系，得到方程（2-80）：

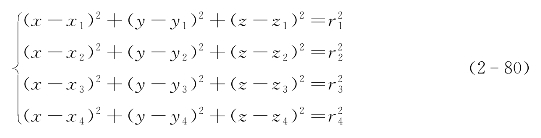
由于现有的潜器多搭载深度计等高精度深度测量装置，故可依照深度是否已知，按以下两种方法求解方程（2-80）。

若目标深度已知，z＝h，则式（2-80）化简可得式（2-81）：

其中，，i＝1，2，3，4。将方程组（2-81）写作矩阵形式AX＝B，当矩阵AA T非奇异时，得到方程的最小二乘解为：

若目标深度未知，方程（2-80）化简可得式（2-82）：

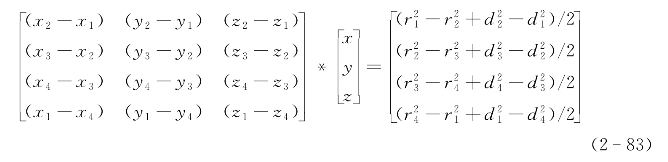(www.daowen.com)

方程组（2-83）同样可记作AX＝B，若矩阵A非奇异，目标的坐标也可通过式（2-82）求得。当4只信标共面时，矩阵A奇异，式（2-83）无解。

2．3．1．2　长基线定位系统导航应用分析

对于AUV等水下潜器，通常由导航系统、机动系统、观测系统等多部分组成总系统，长基线定位系统是导航系统与声学系统的交联部分。声学系统由声通信机、ADCP／DVL、侧扫声呐等设备构成。定位系统使用的询问／应答信号，多是低频的宽带编码信号，在工作频率上和其他的声学设备通常具有部分重叠。在工作时，需要将相互影响的声学设备安排在不同的工作时刻，以避免各个子系统之间发生信号混叠。

以我国自行研制的某水下潜器为例，在作业时，系统总体的工作周期为N s，在一个周期以内，各声学设备的工作情况如图2-26所示。

图2-26　导航系统中各声学设备工作安排示意图

假设长基线测距单元在0 s时发送询问信号，在N1 s内收到3个或更多的应答信号，即可以通过式（2-82）求得潜器的位置坐标，得到1次长基线的定位结果输出。但系统周期剩余的N2 s长基线系统不工作，只能每隔N s得到一次定位结果输出，降低了长基线定位结果的输出、更新速率。

同时，由方程组（2-81）和式（2-83）可知，长基线的定位结果输出，即使在深度已知的情况下，也需要有3个及以上的声信标时延信息；在深度未知时，则需要多于3个声信标时延信息，这要求测距单元具有较强的信号检测能力，同时要求应答信号具有较强的测时分辨能力和抗噪声能力。如果目标处于某个声信标的作用范围之外或处于应答信号的强叠加区，也会降低长基线定位结果的更新速率。

另外，基于响应模式的长基线定位系统，为水下潜器提供定位时，由于潜器运动和声传播速度较慢引起的信号收发非共点、非共时的问题，也是影响长基线系统定位和导航精度的重要原因之一［16，17］。在长基线对潜器定位时，由安装在潜器上的测距单元周期性发送询问信号，在收到全部声信标的应答信号之后，根据双程传播时延，结合声速，求得测距单元与各声信标之间的距离，进而根据声信标的地理坐标解算出自身的位置。而水下潜器通常处于运动状态，如图2-27所示，潜器在信号“询问→应答”过程中，测距单元在信号发射与接收时刻的坐标不同，因此“潜器→声信标”以及“声信标→潜器”对应的传播时间也并不相同；同时，由于目标与各声信标之间的距离不同，接收不同声信标应答信号的时刻与位置也不相同。常规的长基线定位模型通常忽略目标运动影响，直接将双程传播时延的一半对应的距离值作为距离信息的观测值，由此进行定位解算，得到目标实际坐标，实际是目标发送询问信号位置和接收到各个应答信号位置的加权平均。

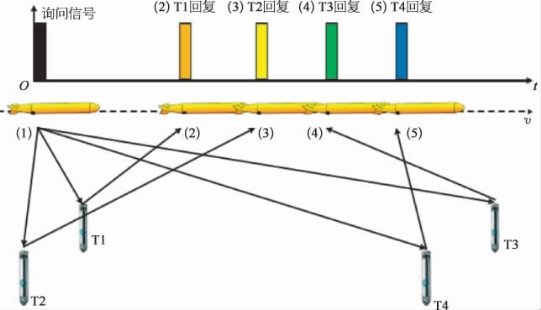
图2-27　潜器运动对长基线定位的影响

针对该问题，学者Detweiler C和Leonard J在文献［18-20］中提出，通过对全局声信标进行联合时间同步替代应答模式，直接获得单程距离值，但长时间工作在深海时，电池寿命和声信标时钟偏移会影响系统工作的持续性和有效性。文献［10］中结合射线声学和贝叶斯反演理论，对声源运动对长基线定位误差的影响进行了仿真，仿真结果显示此时考虑动态时系统的定位误差是静态目标的5倍以上。之后，作者提出将测时残差作为修正量，提出结合目标运动轨迹及声信标基阵坐标进行联合反演的运动补偿算法，该算法要求系统有着至少0．1 ms级的测时精度。

卡尔曼滤波是解决以上问题的有效技术手段之一［21-24］，该方法可通过分析目标运动状态建立运动模型，将目标运动状态，如航速、航向、航姿等信息和声学定位数据进行融合，既可以提高定位结果的更新速率，也可以减小目标运动对定位系统的影响。2012年，Bahr A和Leonard J使用扩展卡尔曼滤波，成功地解决了水下多AUV协同导航时涉及的基线运动问题［2527］。目前卡尔曼滤波已成为工程应用中跟踪目标运动的惯用方法，将多种外部传感器冗余信息有效融合，可以达到单一观测系统不能达到的优异性能。