惯导系统初始对准通常可分为两个阶段:粗对准阶段和精对准阶段。在粗对准阶段确定初始姿态矩阵的大致取值;在精对准阶段,利用导航误差作为观测量,通过失准角误差模型估计失准角,获得准确的姿态矩阵。
2.2.5.1 摇摆基座上粗对准
1)传统解析式粗对准方法
不考虑测量误差,粗对准时航行器静止,加速度计测量比力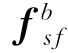 是重力加速度矢量g在b系上的投影g b,且方向相反,即
是重力加速度矢量g在b系上的投影g b,且方向相反,即![]() ;陀螺测量的是地球自转角速度矢量ωie在b系上的投影
;陀螺测量的是地球自转角速度矢量ωie在b系上的投影 。由在对准地点的地理位置已知的前提下,矢量g和ωie在n系中的投影g n和
。由在对准地点的地理位置已知的前提下,矢量g和ωie在n系中的投影g n和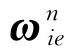 也是已知的。姿态矩阵
也是已知的。姿态矩阵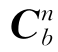 可由g及ωie在b系与n系之间的变换关系求得,即:
可由g及ωie在b系与n系之间的变换关系求得,即:

如果g n和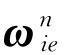 不平行,为了直接求解出
不平行,为了直接求解出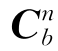 ,可以通过构造新的向量方程来增加方程的数目,由式(2-41)与式(2-42)作叉乘,得:
,可以通过构造新的向量方程来增加方程的数目,由式(2-41)与式(2-42)作叉乘,得:
![]()
将式(2-41)、式(2-42)和式(2-43)分别转置,再组合在一起写成矩阵形式为:
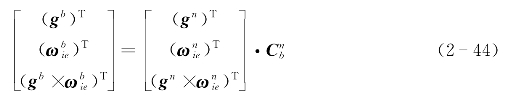
由式(2-44)直接得姿态矩阵:
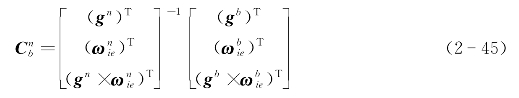
式(2-45)就是传统解析式粗对准方法的计算公式。由于存在干扰和噪声,加速度计和陀螺测量值g b和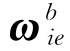 带有一定误差,所以通常采取一段时间内测量值取平均的方法以减小干扰和噪声的影响。如果载车出现较大幅值的晃动干扰,上述粗对准方法可能产生很大误差。比如在低纬度地区,假设粗对准开始时b系与n系重合,即真实航向角ψ=0°,取粗对准时间为60 s,如果粗对准即将结束时出现绕载体oxb轴转动15′的晃动干扰,则有
带有一定误差,所以通常采取一段时间内测量值取平均的方法以减小干扰和噪声的影响。如果载车出现较大幅值的晃动干扰,上述粗对准方法可能产生很大误差。比如在低纬度地区,假设粗对准开始时b系与n系重合,即真实航向角ψ=0°,取粗对准时间为60 s,如果粗对准即将结束时出现绕载体oxb轴转动15′的晃动干扰,则有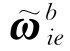 =[15′15′0]T/60 s和
=[15′15′0]T/60 s和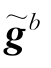 =[0 0-g]T,将其代入式(2-45)可求得到粗对准结果
=[0 0-g]T,将其代入式(2-45)可求得到粗对准结果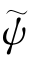 =315°,显然这个结果是错误的。
=315°,显然这个结果是错误的。
2)摇摆基座对准算法
为了方便描述算法,这里定义一种新的坐标系——载体惯性坐标系(ib0系):在粗对准开始时刻(t0时刻)将b系在惯性空间中固化成为ib0系,即ib0系的原点为在t0时刻载体的重心,且不随载体重心的移动而移动,oxib0、oyib0、ozib0轴分别与t0时刻b系的同名坐标轴重合,且在惯性空间中保持指向不变。
初始对准姿态矩阵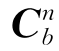 可用如下矩阵连乘形式表述:
可用如下矩阵连乘形式表述:
![]()
式中,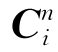 为t时刻i系与n系之间的变换矩阵,可由载车所在点地理位置及粗对准时间t确定;
为t时刻i系与n系之间的变换矩阵,可由载车所在点地理位置及粗对准时间t确定;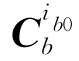 为t时刻b系与ib0系之间的变换矩阵,利用陀螺输出的b系相对ib0系的角运动信息,通过捷联惯导姿态更新算法可以求得该矩阵;
为t时刻b系与ib0系之间的变换矩阵,利用陀螺输出的b系相对ib0系的角运动信息,通过捷联惯导姿态更新算法可以求得该矩阵;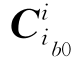 为ib0系至i系之间的变化坐标矩阵,该矩阵是个常值阵,可由重力加速度与加速度计输出之间的转换关系求得,该矩阵的计算是求解姿态矩阵
为ib0系至i系之间的变化坐标矩阵,该矩阵是个常值阵,可由重力加速度与加速度计输出之间的转换关系求得,该矩阵的计算是求解姿态矩阵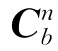 的关键。以下详细介绍上述三个变换矩阵的求解算法。
的关键。以下详细介绍上述三个变换矩阵的求解算法。
(1)求解变换矩阵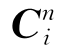 。
。
变换矩阵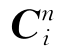 可由n系相对于e系的位置矩阵C ne和e系相对于i系转过的角度ωiet求得,即:
可由n系相对于e系的位置矩阵C ne和e系相对于i系转过的角度ωiet求得,即:
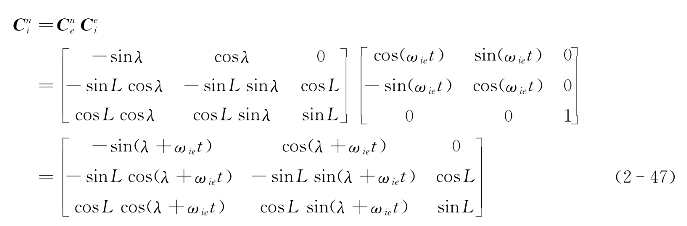
(2)求解变换矩阵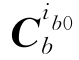 。
。
变换矩阵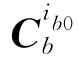 可通过陀螺采样输出,结合捷联惯导姿态更新算法求得。设tk时刻和tk+1时刻的变换矩阵
可通过陀螺采样输出,结合捷联惯导姿态更新算法求得。设tk时刻和tk+1时刻的变换矩阵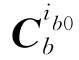 分别为
分别为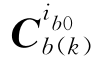 和
和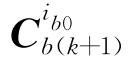 ,其对应的变换四元数分别为
,其对应的变换四元数分别为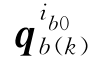 和
和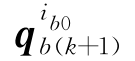 ,显然有
,显然有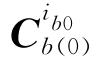 =I和
=I和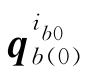 =1,再假设tk时刻至tk+1时刻陀螺输出的角增量为Δθk,则利用等效旋转矢量单子样算法可得b系相对于ib0系从tk时刻至tk+1时刻的变换四元数为:
=1,再假设tk时刻至tk+1时刻陀螺输出的角增量为Δθk,则利用等效旋转矢量单子样算法可得b系相对于ib0系从tk时刻至tk+1时刻的变换四元数为:
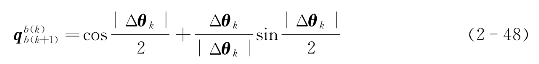
从而可进行四元数更新解算:
![]()
最后,假设![]() 则由变换四元数和变换矩阵之间的关系(2-47)式,可计算得tk时刻的变换矩阵
则由变换四元数和变换矩阵之间的关系(2-47)式,可计算得tk时刻的变换矩阵![]() 。
。
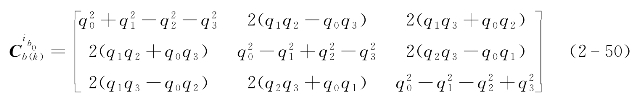
变换矩阵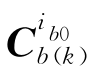 的更新解算使得粗对准具有了跟踪载体角运动的功能,也就是说式(2-46)获得的是粗对准结束时刻的姿态矩阵。
的更新解算使得粗对准具有了跟踪载体角运动的功能,也就是说式(2-46)获得的是粗对准结束时刻的姿态矩阵。
(3)求解变换矩阵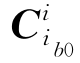 。
。
变换矩阵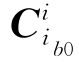 是个常值矩阵,当载车静止时,该矩阵可由重力加速度在i系的投影g i与加速度计输出在ib0系的投影
是个常值矩阵,当载车静止时,该矩阵可由重力加速度在i系的投影g i与加速度计输出在ib0系的投影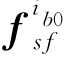 之间的转换关系求得,即:
之间的转换关系求得,即:
![]()
其中,

在式(2-51)中取两个不同的时间点,tl时刻和tm时刻(l<m)的变换方程,并类似于式(2-41)—式(2-45)的方法可得:
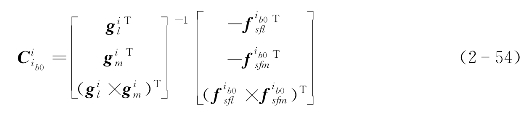
当tl时刻与tm时刻间隔较小时,上式中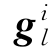 和
和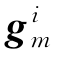 几乎平行。为了降低计算误差应使tl适当远离tm,例如可取tl为粗对准起始时刻而tm为结束时刻,但是,扩大tl与tm间隔就必然增长了粗对准时间。
几乎平行。为了降低计算误差应使tl适当远离tm,例如可取tl为粗对准起始时刻而tm为结束时刻,但是,扩大tl与tm间隔就必然增长了粗对准时间。
由于惯性器件噪声等随机干扰的存在,应对式(2-51)在tl时刻和tm时刻附近积分,以降低干扰的影响。设tk时刻至tk+1时刻陀螺输出的角增量为Δθk,加速度计输出的比力速度增量为Δvk,类似于捷联惯导速度更新算法,利用速度单子样算法由式(2-41)可得在ib0系上投影的速度更新算法
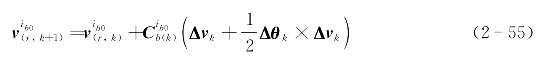 (https://www.daowen.com)
(https://www.daowen.com)
其中![]() ,并且有
,并且有![]() =0。
=0。
另外,将式(2-47)代入式(2-53)并从tr时刻至tk时刻积分可得:
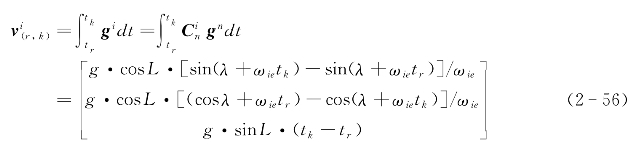
取t0<tu≤tv<td,其中t0为粗对准开始时刻、td为粗对准结束时刻,则将式(2-51)两边都积分可得:

式中,![]() 和
和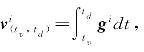 并用类似于式(2-41)~式(2-45)的方法可得:
并用类似于式(2-41)~式(2-45)的方法可得:
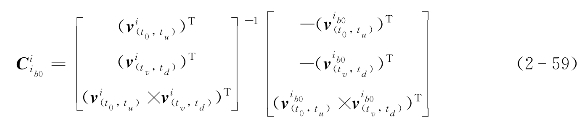
最后,将式(2-47)、式(2-50)和式(2-54)代入式(2-46)即可求得粗对准姿态矩阵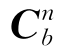 。
。
2.2.5.2 利用航位推算进行运动中精确对准
1)几何方法对准基本原理
利用姿态传感器测量航行器的姿态,而航向角可以在水面上使用两个位置点进行测量,当两个位置点相距几公里时,可以忽略它们之间较小的纵向距离,把它们看作是在同一水平面上,例如,图2-20所示平面上有点P0(x0,y0)和P1(x1,y1)。
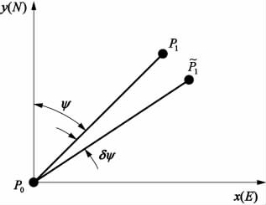
图2-20 几何对准基本原理
则由它们确定的基线与北向之间的夹角(主值)为:
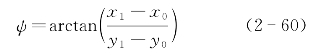
在利用航位推算进行精细对准时,不是直接由已知两点的位置求取精确的航向角,而是利用航位推算位置![]() 和已知位置P1(x1,y1)之间的误差求得航向误差角δψ,再对航向角进行修正。如果忽略其他误差,如陀螺漂移和DVL刻度系数误差等,仅考虑初始航向误差角,则由于航向误差角的影响,航行器航行一段距离后将出现位置误差。假设航行器沿直线航行并且初始航向误差角是小角,则可计算得初始航向误差角近似为:
和已知位置P1(x1,y1)之间的误差求得航向误差角δψ,再对航向角进行修正。如果忽略其他误差,如陀螺漂移和DVL刻度系数误差等,仅考虑初始航向误差角,则由于航向误差角的影响,航行器航行一段距离后将出现位置误差。假设航行器沿直线航行并且初始航向误差角是小角,则可计算得初始航向误差角近似为:

上式中正负号视具体情况而定。因为航向误差角在航行器P0P1航行过程中基本不变,所以利用该误差角实时修正P1点处的航向角,而不是初始粗对准时P0点处的航向角,就完成了航向角的精对准过程。
2)航位推算轨迹和真实轨迹相似法
和纯惯性导航算法相比,在航行器航位推算系统中速度和位置计算误差都比较小,如果陀螺漂移很小或者航行器行驶时间较短,可认为姿态误差角和DVL刻度系数误差在航行器行驶过程中为常值φ和δKD,则可得:
![]()
其中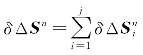 为航位推算累积位置误差,
为航位推算累积位置误差,![]() 为位移。通常水平姿态误差角φE和φN都比较小,如果进一步忽略它们的影响得:
为位移。通常水平姿态误差角φE和φN都比较小,如果进一步忽略它们的影响得:
![]()
其中,记[·]3=[0 0·]T,φU为天向姿态误差角。
由式(2-63)在水平面上投影可得:
![]()
实际上,只要将式(2-63)中δΔS n和ΔS n的第三分量都置为0并分别记为δΔS h和ΔS h,即得式(2-64)。
为了方便说明问题,提出两折线相似概念:oxy平面上两条折线r和r′分别由线段didi+1和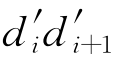 首尾相连组成(其中i=0,1,2,…,下同),并且r和r′具有共同的起始点,即d0和d′0重合,连接起始点到端点di和
首尾相连组成(其中i=0,1,2,…,下同),并且r和r′具有共同的起始点,即d0和d′0重合,连接起始点到端点di和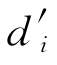 的矢量分别记为ri和
的矢量分别记为ri和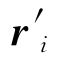 ,如果长度之比
,如果长度之比![]() 为常值,并且ri到
为常值,并且ri到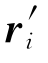 的转角β也是常值,则称这两条折线相似,如图2-21所示。换言之,如果折线r′和r相似,则可以由r构造出r′,即由ri绕d0转动β角再乘以比例系数k则得
的转角β也是常值,则称这两条折线相似,如图2-21所示。换言之,如果折线r′和r相似,则可以由r构造出r′,即由ri绕d0转动β角再乘以比例系数k则得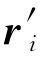 。假设d0为原点,ri和
。假设d0为原点,ri和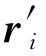 的坐标分别为(xi,yi,0)和
的坐标分别为(xi,yi,0)和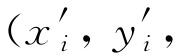 0),且β角是小角,则两矢量ri和r′i之差为:
0),且β角是小角,则两矢量ri和r′i之差为:
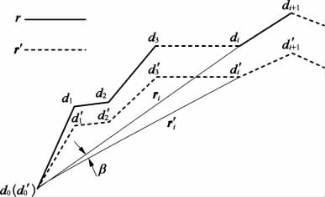
图2-21 折线相似示意图
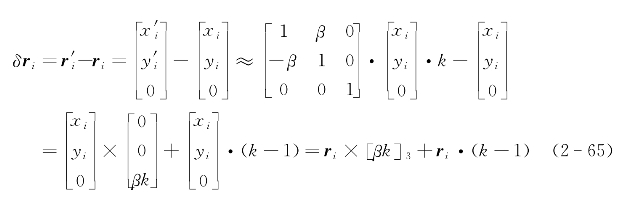
比较式(2-64)和式(2-65)可知,在水平面上投影时航位推算轨迹和航行其行驶过的真实轨迹是相似的,这就是航位推算轨迹和真实轨迹相似性原理。
3)航向误差角的计算
利用航位推算轨迹和真实轨迹相似的特点,在航行器行驶过程中可实现航向误差角的修正,即进行精对准。由起始点和位置已知点间的矢量水平投影ΔS h和航位推算矢量水平投影 ,利用简单的几何关系,可求得转角,即天向姿态误差角φU:
,利用简单的几何关系,可求得转角,即天向姿态误差角φU:
![]()
移项整理近似得:
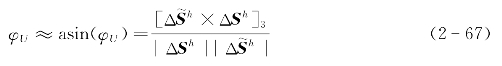
由此可见当水下航行器航行到位置已知的位置点时(如露出水面接收GPS定位信息),由航位推算位置误差和航行器位移可求得误差角φU,因此在位置已知点估计出φU后,只要将计算航向角直接减去估计出的φU即可得到精对准航向角。这就是利用了航位推算进行精对准的方法。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






