由捷联惯组可单独构成SINS，并利用捷联惯组中的姿态矩阵与水下航行器上的多普勒测速仪（DVL）可构成航位推算系统，再利用这两个子导航系统一起组成组合导航系统，结构框图如图2-1所示。

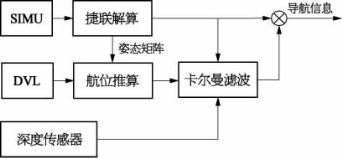
图2-1　SINS／DVL组合导航系统原理图

DVL是用来测量水下航行器航行速度的仪器，它不能单独用于确定位置，但是可以从惯导系统中获得方位信息，进行航位推算，组成航位推算系统（dead reckoning，DR）。

SINS／DVL组合导航系统的高度定位误差是发散的，因此有必要借助于深度传感器的阻尼作用，提高系统高度通道的定位精度。

假设捷联惯组中陀螺漂移误差为随机常值漂移εb、加速度计偏置误差为随机常值偏置Δb，多普勒测速仪刻度系数误差为随机常值δKD，如下定义19维状态向量：

其中，φ为捷联惯导姿态误差角，δv n为捷联惯导速度误差，δp为捷联惯导位置误差，δpD为航位推算位置误差；SINS／DVL组合导航系统误差方程可以表示成：

式中，

式中，w为系统状态噪声，G为噪声分配矩阵。

以捷联惯导解算位置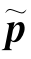和航位推算位置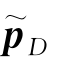之差值作为卡尔曼滤波器的观测量，即定义观测量：

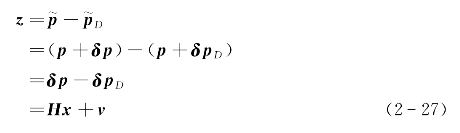
其中，p表示载车的真实位置，是一个未知量，H＝［03×6　I3×3　03×6　－I3×3　03×1］，v为测量误差。

式（2-25）和式（2-27）为SINS／DR组合导航系统卡尔曼滤波模型方程。

经过编制轨迹发生器，轨迹运行主要参数如图2-2、图2-3所示，该轨迹机动主要包含航向转弯和水平加速度，轨迹最大速度为20 m／s，总路程约13 km，行驶时间1 200 s。

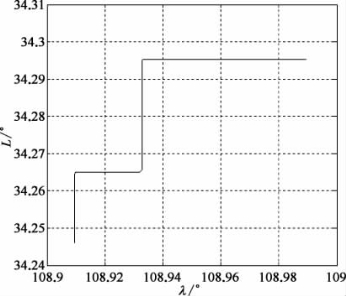
图2-2　水下航行器行驶轨迹

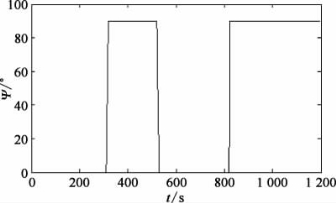
图2-3　水下航行器航向角变化

SINS／DVL组合导航系统有关误差源设定如下：

①陀螺随机常值漂移0．02°／h，噪声0．01°／h；加速度计随机常值零偏1×10－4 g，噪声1×10－5 g；DVL刻度系数误差为0．2%；(www.daowen.com)

②捷联惯导初始对准水平姿态误差角1′、航向误差角10′；初始经纬度和高度误差均为10 m；

③经纬度测量噪声均方差均为0．1 m／Re，高度测量噪声均方差为0．1 m。

SINS／DR组合导航系统仿真结果见图2-4～图2-11。为了便于比较，图2-11还给出了单独采用航位推算算法的仿真结果。从仿真中可以得出以下几点结论：

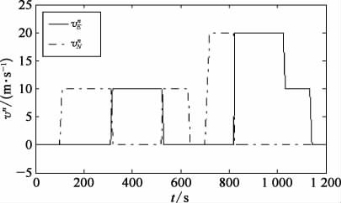
图2-4　水下航行器水平行驶速度

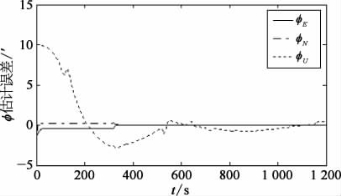
图2-5　姿态误差角估计误差

①比较图2-6和图2-10，SINS／DR组合导航系统位置误差小于单独的DR位置误差，1 200 s时前者误差约10 m，而后者误差大约50 m。SINS／DR组合导航位置误差小的原因主要在于：组合导航系统中航向误差角和DVL刻度系数误差能被较好地估计出来。图2-10表明，航向误差角在约200 s后得到比较充分的估计，估计误差为1′～3′，小于初始航向误差角10′，实现SINS／DR组合导航算法在运动条件下的精确对准。从图2-11中可以看出，在100 s航行器加速后，DVL刻度系数误差获得了较好的估计效果，估计误差约为0．01%。另外，图2-7显示了水平陀螺随机常值漂移估计效果不错，而天向陀螺漂移基本没有估计效果；图2-8显示了天向加速度计随机常值零偏很快就获得了准确估计，在310 s航行器转弯时水平加速度计零偏也得到了较好的估计。

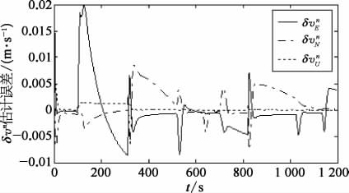
图2-6　速度估计误差

图2-7　位置估计误差

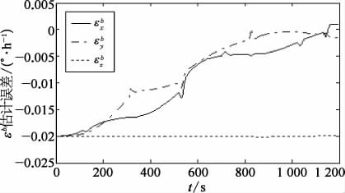
图2-8　陀螺随机常值漂移估计误差

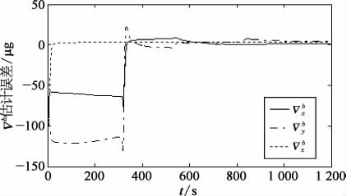
图2-9　加速度计随机常值零偏估计误差

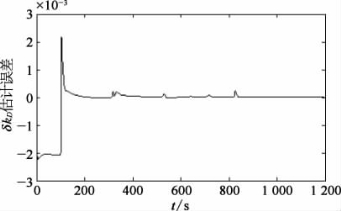
图2-10　DVL刻度系数误差的估计误差

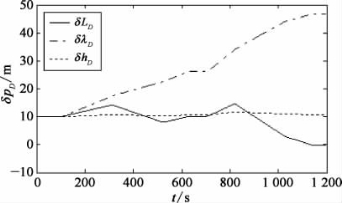
图2-11　单独航位推算的位置误差

②和SINS／GPS组合导航系统相比，SINS／DR组合导航系统位置误差是有偏的。在SINS／GPS组合导航系统中，可以认为GPS定位误差是零均值的白噪声，GPS在抑制SINS位置误差发散的同时，SINS对GPS位置误差起着平滑作用，因此可以认为SINS／GPS组合导航系统的位置误差也是零均值的噪声，可谓该误差是无偏的。而在SINS／DR组合导航系统中，航位推算系统和SINS有相同的误差源（如姿态误差角和初始位置误差），并且航位推算误差会随航行器航程不断累积，对于初始位置误差和在导航过程中产生的位置误差将是不可被估计和消除的，所以SINS／DR组合导航系统的定位误差是有偏的。图2-6显示了SINS／DR组合导航系统不能估计出初始位置误差。

③参见图2-6和图2-10，航位推算和SINS／DR组合导航两种算法中高度误差发散都很小。在仿真算法中未考虑捷联惯组俯仰安装误差角的影响，认为捷联惯组标定坐标系和DVL坐标系始终重合，并且初始对准水平姿态误差角不大（远远小于航向误差角），所以两种算法中高度误差变化都比较小。而实际系统中由于捷联惯组标定坐标系和DVL坐标系间存在俯仰安装误差角，高度通道误差可能较大，呈现发散趋势。