捷联惯导系统（strap-down inertial navigation system，SINS）具有自主导航能力，不需要任何外界电磁信号就可以独立给出载体的姿态、速度和位置信息，抗外界干扰能力强，但是SINS定位误差随时间的延续不断增大，即误差积累、漂移增大。

惯导系统具有一定的互补性，由它们构成的组合导航系统能在一定程度上有效抑制惯导系统误差随时间的发散，因为惯导系统误差随着导航时间而增长，而多普勒速度仪测量误差一般随着运载体行驶距离而积累；利用惯导系统短时间导航的高精度特性，在机动条件下能够对多普勒速度仪测量误差进行一定的校正。此外，利用深度传感器能准确确定水下航行器的深度定位信息。因此水下航行器自主定位定向系统可以由以下几部分组成：捷联惯组、多普勒测速仪、深度传感器等。其中，捷联惯组包括三个陀螺和三个加速度计，是实现水下航行器自主定位导航功能的关键部件。

2．2．1．1　捷联惯导系统误差方程

1）捷联惯导系统中常用的坐标系

（1）地心惯性坐标系（i系）。

用oxiyizi表示；原点为地球中心；xi、yi轴在地球赤道平面内；xi轴指向春分点（赤道面与黄道面的交线再与天球相交的交点之一），春分点是天文测量中确定恒星时的起始点；zi轴为地球自转轴，并指向北极。惯性器件（陀螺和加速度计）的输出就是以惯性坐标系为参考基准的。

（2）地球坐标系（e系）。

用oxeyeze表示；原点为地球中心；xe、ye轴在地球赤道平面内；xe指向本初子午线；ze轴为地球自转轴，并指向北极。e系与地球固连，地球坐标系相对于惯性坐标系的角运动就是地球的自转角速度ωie＝15°／h。

（3）地理坐标系（g系）。

用oxg ygzg表示；原点为载体重心；xg轴指向东，即E；yg轴指向北，即N；zg轴指向天，即U。地理坐标系相对于地球坐标系的方位关系就是载体的地理位置（经度λ和纬度L）。

（4）导航坐标系（n系）。

用oxnynzn表示；它是惯导系统在求解导航参数时所采用的坐标系，本书选取东—北—天（ENU）地理坐标系作为导航坐标系。

（5）载体坐标系（b系）。

用oxb ybzb表示；原点为载体的重心；xb轴沿载体横轴向右；yb轴沿载体纵轴向前；zb轴沿载体立轴向上。b系与载体固连，载体坐标系相对于导航坐标系的方位关系可用载体的姿态矩阵表示。

2）捷联惯导系统误差方程

（1）姿态误差方程：

（2）速度误差方程：

（3）位置误差方程：(www.daowen.com)

将它们整理成：

其中，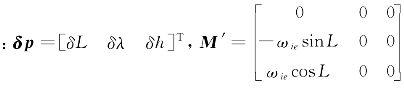

假设捷联惯组经过严格标定以后陀螺标定误差矩阵δKG和加速度计标定误差矩阵δKA均很小，可以忽略它们的影响，并假设陀螺漂移误差为随机常值漂移、加速度计偏置误差为随机常值偏置，如下定义15维状态向量：

则捷联惯导系统误差方程可表示为：

式中，

2．2．1．2　航位推算误差方程

利用多普勒测速仪输出在导航坐标系（n系）中进行定位解算，假设捷联惯组标定坐标系与载车坐标系重合安装，则多普勒测速仪的速度输出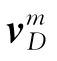在导航坐标系上可表示为：

和捷联惯导位置更新算法微分方程式一样，可得航位推算定位解算的微分方程：

其中，LD、λD和hD分别为航位推算定位解算的纬度、经度和高度，并且＝。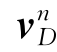

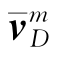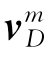假设多普勒测速仪的测量误差主要为刻度系数误差δKD，则多普勒测速仪测量的实际速度大小和理论速度之间的关系为：

所以，实际测量中多普勒测速仪测量的速度输出在导航坐标系上表示为：

其中，φD为水下航行器的姿态误差角，展开上式并略去关于φD和δKD的高阶小量得：

将式（2-16）代入式（2-11），得速度误差方程：

类似于SINS位置误差方程，由航位推算位置微分方程式（2-12）、式（2-13）、式（2-14）可直接写出位置误差方程：

上式写成矩阵形式记为：

其中，，δpD＝［δLD　δλD　δhD］T，

再将式（2-17）代入式（2-19）得航位推算位置误差方程：