除了仔细开发的模型外，合理组织证据对于处理容错系统演绎性验证的复杂性是必不可少的。接下来描述的技术，包括把目标分解成易于管理的步骤的方法及应用专门的证明技术。

15.4.1.1 精细化

为了便于推导，一般都将形式化证明分解成一系列的小步骤。这种方法的一个案例是精细化风格的演绎法，即一开始通过一个抽象的形式指定所需的属性，然后根据对一些实体的抽象模型的假设，证明该属性的正确性。随后，更多的细节被添加到这个初始的抽象模型上，例如，提供某些抽象实体的具体诠释。然后，通过证明详细的解释满足抽象论据依赖的假定，针对精细化模型也拥有理想属性的证明可以从抽象模型那里继承下来。

中央的守护者的容错属性分析在基于星形TTA系统中遵循这个总体方案^[28]。为了证明中央守护者延伸可以被系统承受的故障类，开发了一系列的、分层方式组织的形式化模型。

每个模型为证明所需属性的正确性推动一小步。每个步骤本身是基于一组假设或先决条件，并在每个模型层i，建立以下形式的定理。

我们的想法是以这样的方式设计不同的模型，造成在一个层次上的属性建立下一层次的假设。最终，这些模型集成、推理结合起来，从而产生大致像下面类型的连锁影响：

最终属性properties_f对应TTP/C通信所需的正确主属性，而最初的假设as-sumption₀描述了构成基本故障的内容。

最抽象模型描述了由节点接收的信息。在这里，节点为了判断所接收的信息正确性而采取各种动作被形式化了。这相当于考虑发送时间和信号编码信息，以及多项一致性检查的输出。然后，通信的主要正确属性是通过这些概念表示的。这个模型层假设关注有关功能要求。特别的是，它们描述了信道发送信息的属性，比如信号编码或传输时间，并反映通信网络可能发生故障的假设。在本质上，这个模型建立了一个命题，可以不完全表示为：

下一层次通过不配置守护者的通道建立了信息传输模型。接着，目标是获得基本假设模型，正如general_channel_properties表达式所覆盖的。然而，为了这样做，一个有关节点可能的故障类型的强力假设是必要的。例如，这个很强力的故障假设要求即使故障的节点也不能在超出本身时槽的时间内数据，且当节点没有被调度发送数据时，节点从来不发送正确信息。

采用的守护者将任意节点故障转换成由故障模型所涵盖的故障。因此，强力的故障假设可以被替换成较弱的有关守护者正确行为的假设。守护者的功能和属性在第三种层次结构模型中进行了正式规定，建立了以下关系：

守护者模型是通用的，例如，它并没有规定在通信网络中使用的守护者类型。最后一级的层次结构为两个典型TTP/C网络的拓扑结构中的每一个都建立了模型：总线拓扑结构和星形拓扑结构。对于前者，每个网络节点都配备有自己的本地总线守护者，每个通道一个；而后者守护者被放置在通道的中央星形耦合装置内。在此模型层次中，显示出守护者的属性是独立于选择的特定拓扑结构，它给出了本地总线的守护者和中央守护者实施相同的算法。因此，下面的关系成立：

15.4.1.2 通用性验证

类似于精细化的验证策略是“通用性验证”策略。正如在精细化的方法中的一样，研究了一种问题抽象化形式，且正确性的证明是基于某些抽象假设。然而，不同的是这个抽象模型的目的是覆盖一整类类似问题。在这个意义上说，验证是通用的，因为它对各种类型的实施是有效地，并假定它们满足抽象假设。

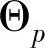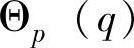已经采用这种分析方法分析了TTP/C的时钟同步算法，且在验证时钟同步的漫长历史发展中，该算法与其他算法遵循类似的发展历程。Schneider观察到平均算法的参数正确性是非常相似的。这一类算法可以通过引入一个收敛函数Cfn的概念，用抽象的方式来捕获，从而描述对节点物理时钟调整的计算方式。为了进行重新同步，节点p必须以某种方式获得其他节点时钟读数的估计值，且结果存储在一个数组中。则值表示q点读数在重新同步时p的估计值。把收敛函数应用到这个时钟读数的数组中，因而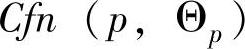就是新的、修正后p的时钟读数。该值和p时钟的当前读数之间会产生差异量，p据此调整其时钟。

Schneider陈述了若干种相当普通的收敛函数假设，并表明它们足以证明一些平均算法的正确性。随后，Shankar使用EHDM系统机械地验证了Schneider证明^[31]，且Miner^[32]进一步改进了约束和证明自身的组织。

时钟同步的协议属性声明：任何时候任何两个无故障节点p和q的时钟读数之差由一个固定的值Δ界定：

协议属性的证明，一般可以通过在一定数量的重新同步的时间间隔上的数学推导来完成。推导假设声明：在每个间隔的开始，任何两个时钟之间的偏差由Δ₀＜Δ界定。然后，证明了下一个时间间隔，在此期间时钟读数可能相互偏离，但其偏差不超过Δ。最后，必须证明应用收敛函数将带来时钟再次更紧密接近，因此，下一个时间间隔以时钟落在另一个Δ₀范围内开始。后一步骤是较难证明的一步；前一步骤对最大精度施加了确定性的约束，对于时钟的漂移率和同步间隔的长度，可以取得给定的具体值。

Schneider的假设本质上是用一种通用方式表达这些属性在完成协议的证明步骤中是必需的。它们中的一些关注涉及同步算法的不同数量之间的相互关系，比如假设的时钟漂移率或当估计远程节点时钟时造成的最大误差。更重要的假设关注时钟同步算法运用的收敛函数的特性。在大多数情况下，这些条件的用处是归于它们从其他概念比如故障成分中分离出了纯数学属性。

中心假设之一被称为精度增强，并用于界定两个应用收敛函数之间的偏离。实际的界限取决于估计的时钟读数数组中的值之间的偏差。存在两个这样的列阵θ和γ（分别用于两个节点p和q），精度增强声明应用p和q的收敛函数的绝对值差不超过Π（X，Y），假设θ和γ中的对应项相差不超过X，且θ和γ变化的范围落在Y内。此外，Π（X，Y）＜Y对于真正提高精度是必需的。

精度增强原理：对于n个节点，存在这样一个集合C，|C|≥n-f，其中f是容错数，存在一个边界Π（X，Y），使得：

如果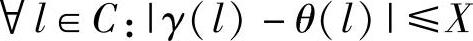

和

那么|Cfn（p，θ）-Cfn（q，γ）|≤Π（X，Y）

精度增强的条件涉及n个节点的子集C，其读数储存在数组θ和γ中。C的元素必须满足精度增强的先决条件，且要求C中至少有n-f元素。对于可以容忍故障f的算法，重要的是n至少是3f＋1（详见参考文献[33]）。这确保了收敛函数中两个节点使用的一组读数可以重叠。(www.daowen.com)

C的直观的解释是一组非故障时钟读数的集合。然而，所列的属性并不直接执行C的解释；实际上，在故障和非故障时钟之间没有做出区别。在这样方式下，Schneider模型也适用于同步协议——可以使用故障时钟读数，或可能舍去非故障时钟的读数——正如TTP/C算法采用的方法——但保证了实际使用的读数满足一定的数学约束。

Schneider模型的一般结果应用于TTP/C的时钟同步的算法，分三个步骤进行。首先，开发的算法基础模型紧跟在非正式协议规范的定义之后。在中间步骤，将基础模型转化成等价的、但更抽象的版本，它依据Schneider的通用概念描述了时钟同步算法的内容。最后，抽象模型中所述的同步算法被证明确实满足各种条件下的Schneider模型的通用证据。

TTP/C算法形式化分析中的关键步骤之一，是定义在精度增强定义中提及的集合C的适当的解释。传统意义上，集合C被解释为非故障节点的集合。这种解释在故障假设——在任何时间至多有f节点是故障的——之下是可行的。在这一定义背后的定理是隐含的假设，即节点可以仅用很小的误差取得非故障节点的时钟读数，且当从相同的非故障节点读取时钟时，两个节点得到的结果大致相同。时钟读数的重要方面即精度增强强调定义的先决条件，是其质量，而非起源。由于TTP/C的算法中的一个节点只保留已经接收到的数据中的最后四个节点的读数，所以不能取n作为系统的节点数量，且用C表示非故障节点的集合。这就是无法建立合适的界限X和Y的原因，因而精度增强先决条件的满足也适用于对于那些非故障节点，其中不存在时钟读数存储在节点队列中。

作为TTP/C的实例，因而C被定义为从任意节点队列中可读取时钟读数节点集合的交集。为了建立TTP/C精度增强的证明，必须证明C至少包含三个元素，也就是说，任意两个非故障结点p和q在各自的列阵中必须具有至少三个公共节点的时钟读数^[29]。

15.4.1.3 分离不变量

组成员的协议属性，即算法在节点之间保持有关其他节点正常运行的一致观点，是不变量，它也称为安全属性，其包含系统所有可达的状态。传统上，这种不变属性的验证需要通过某种形式的归纳证明：一是初始状态（s）保持的属性，以及所有状态转换所保持的属性。然而，所需的性质很少可以归纳，因此，为了建立可以归纳证明的步骤，必须进行通过联合附加属性这样的强化处理。反过来，这些附加属性也必须是不变量。通常情况下，这个过程被重复了好几次才可以完成归纳证明。

Rushby基于算法可能状态的符号前向可达性分析^[35]，提出了一种证明不变量属性的方法。这种方法有利于通过采用分离式变量，建造归纳不变量属性，且这种方法被应用于验证TTP/C组成员算法中^[6]。

从初始状态开始，当节点执行算法的每个步骤时，节点进行的状态更新被反复检查。在每一步骤，所有节点的状态用统一的方式描述，以形成算法的一种特定构造。然后，算法的每一个步骤执行对应于从一种结构转换到另一种结构。配置和转换的集合可以自然地通过示意图（配置示意图）来说明。

系统的配置形成了这个示意图的节点，且箭头表示从一种配置转换到另一种配置，其上的标记称为转换条件。由于每一个转换对应一个引理，它象征声明该算法执行的每一个步骤导致系统从一个配置转换到另一个配置，所以该示意图可以被看做是一大部分正确性属性证明的图形表示。配置通过时间t进行参数化，且配置描述系统所处的全局状态。配置可以拥有附加参数，比如其内部状态不同于系统中其他节点内部状态的节点，或是必须描述系统状态的额外实体。标签的改变表达了系统从一个配置转换到另一个配置的先决条件。从一个结构到另一个结构的转换条件不一定必须是不相交的，但在这个意义上显示它们的分离性是真实的。

通过反复运用以下步骤，可以系统性地开发如TTP/C组成员算法的流程图实现：

（1）首先定义一些初始配置，通常包含所有的初始状态。

（2）选择一种配置，并为它创造一定的转换条件。为此，必须分析该算法来推导出可能采取的算法分支。为了确保覆盖所有的情况，必须证明所有转换条件的分离性是真实的。

（3）然后，对于每一个新的转换条件，在给定的配置下象征地模拟出算法的每一个步骤。

（4）现在要确定模拟结果是否变成一个新的配置，或者它是否是一个变异体，或是一个已经存在配置的推广。在任何情况下，转换的有效性，也就是说该算法从一种配置到另一种确实需要的步骤，必须证明。

（5）针对每个配置和每个转换，步骤（2）～（4）必须重复进行，直到示意图结束。

必须选择这样的配置定义，就是可以证明该算法属性的正确性。这要求每个配置的描述表明所需的安全属性，且要求从任意一种配置到其他配置的转换条件的分离性评价为真的；这可以确保不存在系统能进入的其他的配置。

这个方法有几个好处：配置示意图可以作为一种算法的综合解释，它提供了进一步了解其功能的洞察力，并允许简单的假设分析。在这种分析中，其结果或微小变化的影响，例如对算法本身或对故障模型，可以进行检验。成员算法的结构图形表示可以让人通过示意图追踪变化的影响，以识别算法可能会失败的情况。最后，但并非最不重要的，此算法不依赖于系统的大小，也就是说，所涉及的节点的数目。事实上，由于问题的规模是一个无解释的模型参数，也就是一个固定的、但是任意的值，所以分析任意数目的节点都是有效的。

15.4.1.4 假设-保证推理

由于TTP/C协议组件中服务的紧密集成，所以时钟同步和组成员都依赖于彼此的正确工作。显然，对于准备工作的组成员来说，为了能够发送和接收消息，节点必须同步。同样的，时钟同步也依赖于组成员，因为当收集远程时钟的估计值时，节点只使用来自于同一组的发出者的消息。因此，如果一个特定服务的形式化分析是孤立进行的，且基于其他部分的正确性假设，因为这种循环推理通常是不健全的，所以问题来自于正确的陈述是否有意义。

但是TTP/C有一个逃避，因为循环依赖可以通过根据协议执行的同步间隔进行的分割推理来打破。实际上，对于在第i个区间正常工作的组成员来说，第i个重新同步必须是正确的，而这又依赖于组成员在区间i-1的工作是正常的，以此类推。Rushby^[36]猜想McMillan介绍的证据规则^[37]可以用来完成在假设_-保证形式中组成员和时钟同步正确性的一个综合的证明。McMillan的规则规定，如果：假如另一个属性P₂到t-1时刻始终是正确的，则一个组件X₁保证属性P₁在t时刻是正确的，且反之：假如属性P₁到t-1时刻始终是正确的，则一个组件X₂保证属性P₂在时间t是正确的，那么X₁和X₂的组合保证P₁和P₂的组合也始终为真的。此外，该规则还允许前提和结论都是相对于一些“辅助属性”H的有效性。很容易看出，此规则是如何按照规则被实例化到成员和时钟同步问题上的。

参考文献对综合分析的方法进行了描述^[29]，尽管形式化的证明并没有展示，但确实和推理的风格酷似。我们的目标是要通过归纳法证明，在所有的同步间隔i中，时钟同步和组成员都正常工作，记作cs（i）∧mem（i）。组成员的验证在参考文献中也有介绍^[6]，该文对第二种组合提供了证明。然而，第一种组合更复杂，因为时钟同步的归纳步骤要求节点把时钟调整的计算基于一个足够大的公共信息的集合，它依赖于组会员服务的可用性。这种要求可以通过某种预测cs_req（i）来捕捉，以致时钟同步的归纳步骤实际上读取：

因此，属性cs_req（i）必须根据第i个时间间隔会员的正确性mem（i）来证明。然而，这些事实在不同的抽象层次上表达：后者在不定时的同步系统模型（从时钟同步中抽象）中证明，而前者使用定时同步模型证明。Rushby^[18]表明：不定时的同步模型是定时模型的合理抽象，但证明依赖于同步节点的时钟。因此，为了根据成员的正确性来证明cs_req（i），另外还需要在第i个时间间隔的时钟同步属性：

假如时钟最初被同步，那么总体归纳证明可以通过附加引理来完成^[29]。