不失一般性，流f_k的偏移值的选择是在区间[0，T_k]上执行的。实际上，由于调度的周期性质（更多详情，见参考文献[2]），所以O_k≥T_k的偏移量等于O_kT_k。一旦初始O_k的偏移量被确定，流f_k后续的所有释放时间流就被设定：O_k＋iT_k，i∈N。

随时间扩散的交通流，每个数据流f_k偏移量的选择，使得它的第一帧f_k，1的释放（或发布）尽可能远离其他已经被调度的帧。这是通过：①识别带最小工作负荷的最长的间隔；②并在此时间间隔中间设置f_k的偏移量来实现的。

14.2.4.1 数据结构

因为对于每一个数据流f_k，它的偏移量是在区间[0，T_k]内选择，我们选择基于时间区间[0，T_max]上进行的分析，来分配偏移，其中。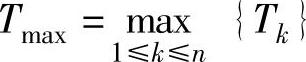

在[0，T_max]区间内，帧的释放时间被存储在列阵R中，R有T_max/g个元素，其中第i个单元R[i]是在可能释放时刻i[也就是在（i-1）g时刻]释放的帧的集合。表14.1为帧流释放列阵R，它对应于交通流的集合Τ＝{f₁，f₂，f₃}，其中f₁＝（T₁＝10，O₁＝4），f₂＝（20，8），f₃＝（20，18）（T_max＝20），同时粒度g＝2。

对于一个给定的帧流f_k，区间是一组邻近的可能释放时刻的集合。

图14.1 NETCAR分析器运行时的屏幕截图。左侧图形是针对不同偏移值设置得到的响应

时间（通过降低优先级）。背景中的电子表格包含：帧的集合、测试的不同偏移设置、对应的WCRT和确定的ECU特性，比如微控制器层面的排队策略（比如FIFO或按优先级）。

表14.1帧流发布列阵R对应于交通流的集合Τ＝{f₁，f₂，f₃}，其中f₁＝（T₁＝10，O₁＝4），f₂＝（20，8），f₃＝（20，18），其分布间隔为[0，20]

定义14.2：对于一个流f_k和时间常量g，可能的发布时刻i和i′是邻近的，当且仅当：

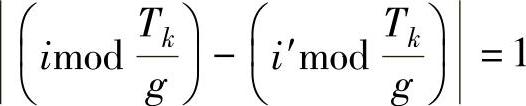
在上述公式中，取模算子告诉我们设置流f_k在可能发布时刻i的偏移量等价于选择可能发布时刻i＋uT_k/g（u∈N）。表14.2显示了f₁的这种定义，其中周期T₁＝10，时间常量g＝2。

这样导致了时间间隔的定义。

定义14.3：对于流f_k，区间间隔是一组有序的可能发布时刻，其中第i和第i＋1个元素是邻近的。这个区间的长度就是有序集合中的单元数。

例如，对于流f₁（见表14.2），集合{4，5，1，2}是邻近可能发布时刻的区间。在这里提到的算法中，我们只考虑到了在相同负载下可能发布时刻的区间。(www.daowen.com)

表14.2邻近的可能发布时刻（在流f₁中，周期等于10）

定义14.4：可能发布时刻i的负载是在i时刻[即在时钟为（i-1）g时刻]对传输调度的发布数。

比如，在表14.1的案例中，可能发布时刻3的负载是1。我们用l_k表示[0，Tk]间隔内的最小负载，最小负载间隔仅仅组成了负载为l_k的可能发布时刻。例如，在表14.1中，l₃等于0，且间隔{10，12}属于最小负载间隔[0，20]。

14.2.4.2 算法描述

我们假定流量通过增加周期值来分类，也就是说，k＜h意味着T_k＜T_h。这种算法循环设置流（从f₁到f_n）的偏移值。让我们考虑分析中的流为f_k。

为f_k设置偏移值，比如使它的第一次发布f_k，1与f_k，1发布前后之间的间隔最大化。具体来说：

（a）在区间[0，T_k]中找到l_k。

（b）在区间[0，T_k]中找到最长的最小负载区间，其中约束可以任意中断。区间中第一个可能的发布时间标记为B_k。

（c）在选定区间的中间设置偏移量O_k，它对应的可能发布时间是r_k。

（d）更新发布列阵R，存储在区间[0，T_max]中发布的f_k的帧：

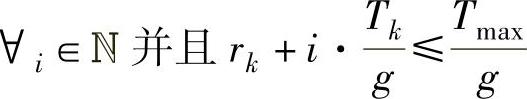
运行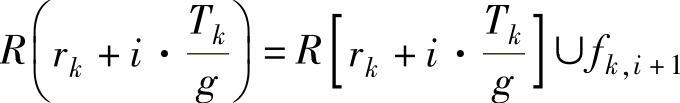

实际中直接在O（n·max_k{T_k}/g）中实施算法，即使有大量的信息也不会产生问题。

14.2.4.3 算法的应用

在我们考虑的案例中，τ＝{f₁，f₂，f₃}，其中f₁＝（T₁＝10，O₁＝4），f₂＝（20，8），f₃＝（20，18），同时时间常数g＝2。首先，算法决定f₁的偏移：l₁＝0[步骤1中（a）]，B₁＝1，E₁＝5[步骤1中（b）]，因此r₁＝3[步骤1中（c）]，这就意味着流的偏移量是4。然后更新列阵R：R[3]＝{f₁，1}，R[8]＝{f₁，2}[步骤1中（d）]。对于流f₂，l₂＝0，选择的区间是{4，5，6，7}，此时B₂＝4，E₂＝7，r₂＝5，R[5]＝{f₂，1}。对于流f₃，l₃＝0，选择的区间是{9，10，1，2}，此时B₃＝9，E₃＝2，r₃＝10，R[10]＝{f₃，1}。应用算法得到的结果见表14.1。