考虑一个包含两个用CAN互联的节点（节点A和B）的简单分布的实时系统。节点A上执行三个任务TA₁、TA₂和TA₃，节点B上执行三个任务TB₁、TB₂和TB₃。节点A上的任务TA₂由CAN帧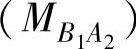的到达而激活，且帧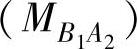是由节点B上的任务TB₁排队的。对称地，节点B上的任务TB₂由CAN帧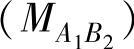的到达而激活，且帧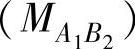是由节点A上的任务TA₁排队的。后一帧比前一帧的优先级更高，但两帧的优先级都比总线上发送的低优先级CAN帧要高。图13.10描述了这个案例。在表13.2中，分别给出了相对于任务TB₁和TA₁发布，任务TA₂和TB₂的截止时间。

为了计算端至端响应时间，我们使用3组耦合方程：一个方程针对CAN总线，一个方程针对每个节点。节点的基本方程为：

R_i＝J_i＋w_i （13.23）

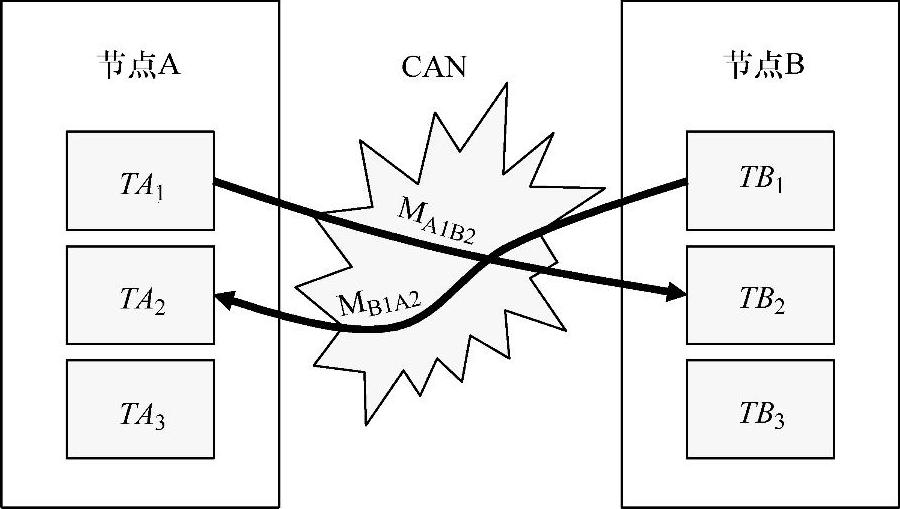
图13.10 案例系统

表13.2 案例系统参数

其中w_i由下式给出：

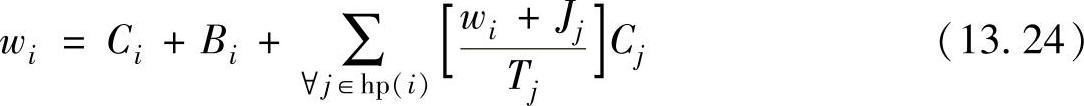
针对CAN总线的方程如下：

R_i＝J_i＋w_i＋C_i （13.25）

其中w_i由下式给出：

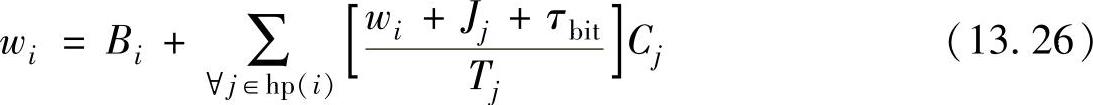
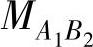按照表13.2中的案例系统，以上两个方程得到实例化。要决定的第一件事就是对在这两个节点上运行任务的优先级进行排序，在这个案例中使用了截止单调优先分配算法^[52]（优化算法可以在文献[22]中找到）。然而，所有的截止时间都未知，因为它们取决于系统部分的时序行为。因此，在某些情况下必须使用最初未实例化的变量。观察未知截止时间，通过向节点B发送CAN帧，任务TA₁结束。该帧将派发任务TB₂，它相对于任务TA₁的派发有长为100的截止时间。由此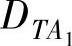，可定义如下：

其中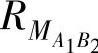，是CAN帧从TA₁发送到TB₂的最坏工况响应时间。(www.daowen.com)

类似地

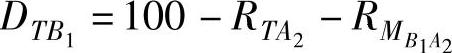
其中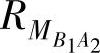，是CAN帧从TB₁发送到TA₂的最坏工况响应时间。未知任务抖动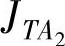取决于帧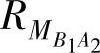到达的变化量，即：

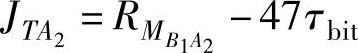
其中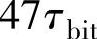，和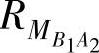分别是最小和最大帧响应时间（相对于任务TB₁的派送）。相似地

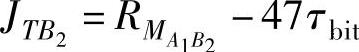
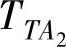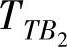在表13.2中唯一剩余的未知量就是任务TA₂和TB₂的周期了。由于它们都是由周期已知的任务（TB₁和TA₁）启动，所以它们会继承这些任务的周期，即＝80以及＝100。

使用上述定义的参数，从节点A开始的可调度性方程可定义如下：

针对节点B任务的方程与节点A的对称：

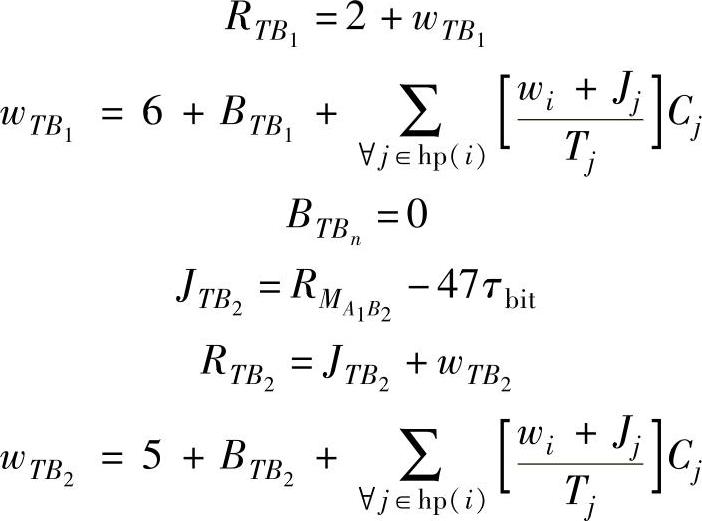
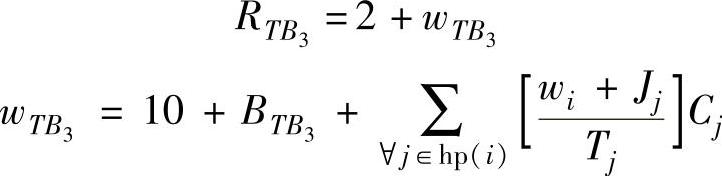
最后组成CAN总线的方程：

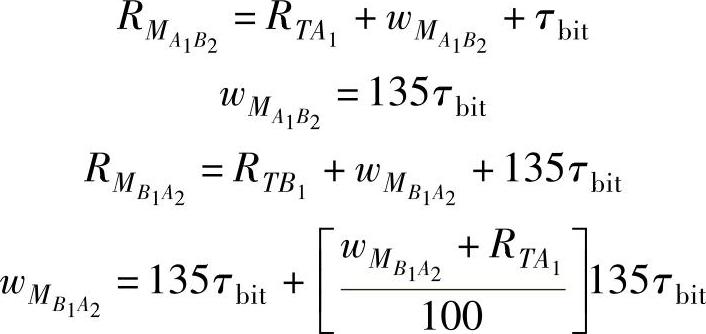
以上是一组可以用迭代法解出的互相依赖的方程，即如果初始时把所有变量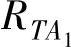、、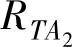、、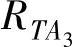、、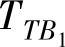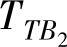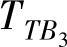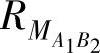及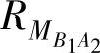设置为0，并在方程中迭代使用这些值，就可以获得新变量值。迭代停止的条件既可以是所有的新值都与上一次的值相等（意味着发现系统可调度），或是超过了任意一个截止时间（可能意味着系统不可调度）。注意优先级会根据截止单调优先分配算法^[52]而更新，因此在迭代过程中，hp（i）可能会改变。更多关于整体调度问题的资料和解法，详见参考文献[53–55]。