前面提到的误差模型非常简单，因此这样是不适合用于描述真实误差的。当确认一个与EMI有关的系统时，我们需要考虑多种误差的来源。仅仅把每个来源分开处理是不够的，取而代之，要把它们综合起来，考虑一个关于总线延迟共同造成的最坏工况干扰。此外，每一个源通常可以通过或短或长的脉冲的信号模式来表征，在此期间总线是不可用的，即在总线上不可能有信号传输。

广义确定性误差模型由普内卡特等^[44]提出，它具有以下特征：

•模拟总线不可用时段期间的干扰时间间隔；

•与丁达尔的误差模型相比，允许指定更多的广义干扰模式；

•允许模拟多种干扰源的合并影响。

根据广义确定性误差模型，E_i（t）基于以下几点定义：

·有k个干扰源，每个干扰源l对误差的贡献项为E^l_i（t）。它们的合并影响为：E_i（t）＝E¹_i（t）|E²_i（t）|...|E^k_i（t），其中∣表示误差项合并记号。本章一般不用加号（＋）来表示误差项的合并。

•每个源l通过在一个特点的时间周期I^l诱导一个未定义的总线值来产生干扰。每个这样的干扰都会导致传输误差。若I^l大于τ_bit，则误差恢复会相应地被延迟。

•每个源l的干扰模式可独立规定为：

–周期为T^l_f的初始脉冲组b^l，其中每组由长度为I^l、周期为t^l_f的n^l个干扰。

–在最初一组脉冲、即b^l*T^l_f之后，每r^l_f单位时间、长度为I^l_f的单一干扰的残余误差率。

图13.9展示的是一个b^l＝4、n^l＝3的单一干扰源的干扰模式。

现在E_i（t）定义为k个干扰源：

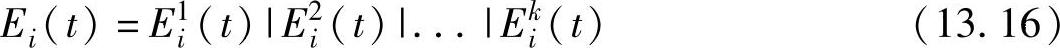
其中

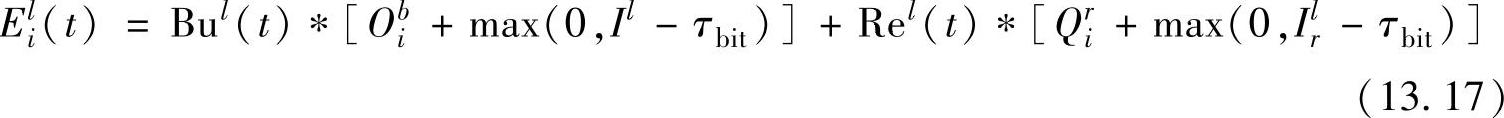(www.daowen.com)

其中

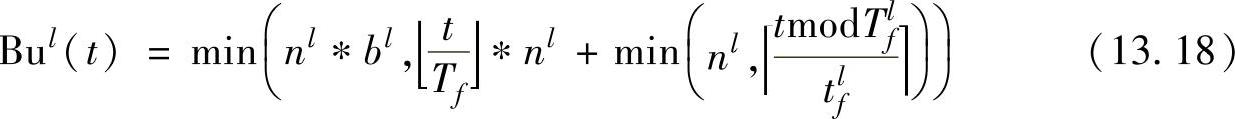
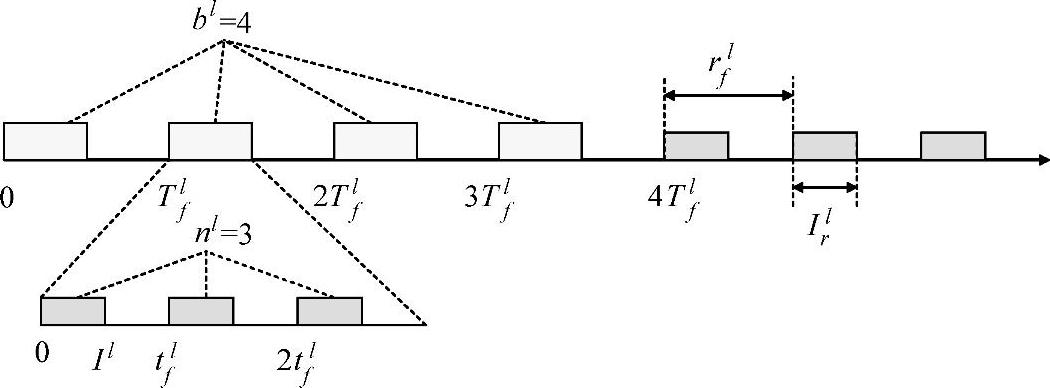
图13.9 带b^l＝4个脉冲、每个脉冲产生n^l＝3个干扰的单一干扰源的干扰模式， 其下面是每r^l_f时间单位的单一干扰的残余误差率

以及

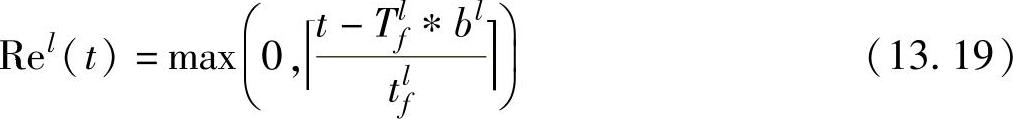
以下给出一些说明：

max（0，I^l-τ_bit）定义了I^l超过τ_bit的长度；

n^l*b^l是最初脉冲周期内产生的最大干扰数；

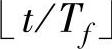是到t时刻为止产生的全部脉冲数；

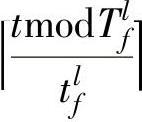是在t时间内适合最后一个脉冲周期（不完整周期）的、长为t^l_f的周期的数目。

在上面E^l_i（t）的公式中，该模型使用不同的上角标来表示脉冲（O^b_i）和单一误差（O^r_i）。用不同上角标因素来表示的优点在于：如果这些因素已知，那么模型会变得更加精确。这会减少尤其是在脉冲条件为O^b_i＞t^l_f时的不利因素，因为在这种情况下我们可以把几个脉冲误差合并成为一个误差，再加上脉冲宽度（Q^s_i＋n^l*t^l_f）。然而，对于许多实际的应用以及在系统设计中，人们会假定脉冲误差和单一误差的上角标相同，都用O_i表示，并由下面公式给出：

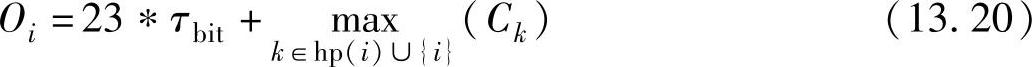
容易知道，丁达尔模型是广义误差模型的特例，有1个误差源（k＝1）、1个原始脉冲（b^l＝1）、带有脉冲误差数为n_error[Bu^l（t）＝n_error]、r^l_f＝T_error以及干扰数I^l＝I^l_r＝τ_bit。然而，在丁达尔的模型中，未规定具体干扰（I^l）持续时间，也没有规定脉冲组的参数（b^l和T^l_f）。