这里举一个有关上述分析的案例，以阐述它们之间的不同之处。更确切地说，在13.5.1节采用的充分响应时间测试中，包含三个帧的集合S被认为是不可调度的，但在13.5.2节中采用的精确响应时间测试中却是可调度的。

考虑表13.1中列出的帧集合。系统的基本假设是总线速度为1Mbit/s，即τ_bit为1μs，且没有排队抖动，即对所有帧，都满足J＝0。所有的帧都有3位有效载荷数据，因此，根据公式（13.3）得到C＝75。总线使用率相当高，达到97%。究其原因是强推一个对于充分分析不适合的细微方案，但它却可以被精确分析捕捉到。

13.5.3.1 充分响应时间测试

充分响应时间测试一开始，对于每个帧i我们使用公式（13.7）计算w_i，并使用公式（13.6）计算R_i，过程如下[回顾一下，公式（13.7）是递推公式，当w^n＋1_i＝wⁿ_i时递推停止]：

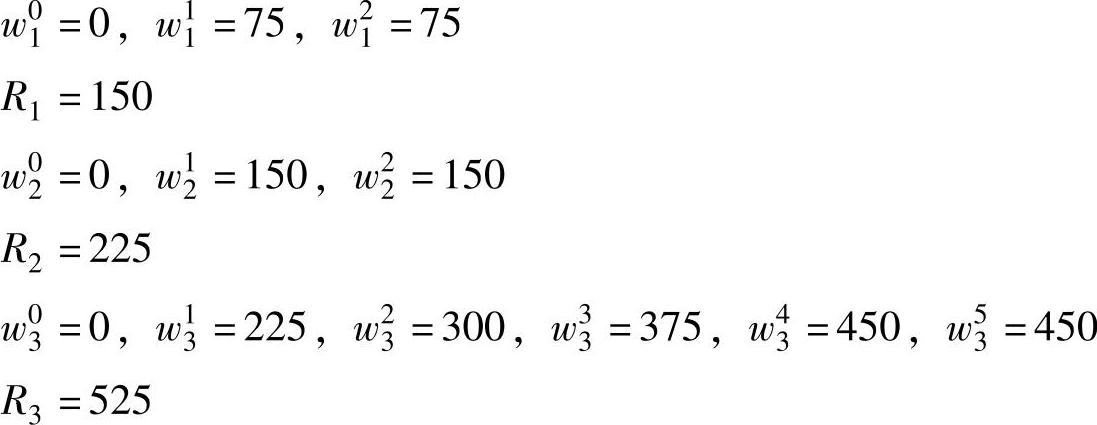
上述结果说明帧1和2可调度，即R₁≤D₁且R₂≤D₂。然而，R₃＞D₃表明错过了截止时间。因此，帧集合S被认为不可调度。

表13.1 帧集合分析

13.5.3.2 精确响应时间测试

相反，使用13.5.2节中的精确分析，上述集合S事实上是可调度的。为了证明这一点，我们使用公式（13.8）～公式（13.12）来计算全部三个帧的帧响应时间。

首先，使用公式（13.8）计算每个级别为i的帧忙时周期，并用公式（13.9）来确认在忙时周期内，该帧是否有多种工况出现。如果确实如此，则用公式（13.10）和公式（13.11）来计算出帧所有出现工况的响应时间，并通过公式（13.12）在这些情况中选出最大响应时间。(www.daowen.com)

从帧1开始，我们用公式13.8计算得到级别为i的忙时周期分别为t⁰₁＝75，t¹₁＝150，t²₁＝150。这样，根据公式（13.9）知Q₁＝1。因此，在帧1的1级忙时周期内，只有一种出现情况。针对这种情况，我们用公式（13.10）和公式（13.11）来计算响应时间：

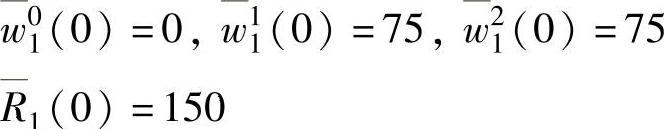
对于帧2，我们用公式（13.8）重复相同的过程，计算出：t⁰₂＝75，t¹₂＝225，t²₂＝300，t³₂＝375，t⁴₂＝450，t⁵₂＝450。

因此根据公式（13.9）得到Q₂＝2，即帧2的2级忙时周期内共有两种情况出现。这里我们要用公式（13.10）和公式（13.11）来计算这两种情况的响应时间，并用公式（13.12）选出最大值：

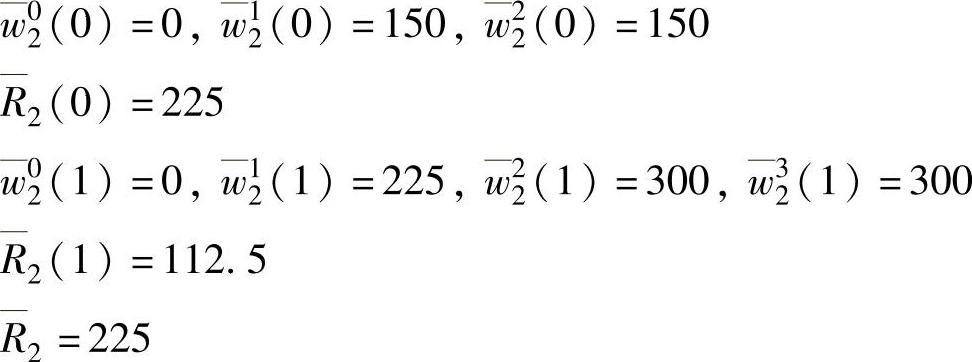
最后在帧3的3级忙时周期内也有两种情况出现：t⁰₃＝75，t₃¹＝225，t²₃＝300，t³₃＝450，t⁴₃＝525，t⁵₃＝525并且Q₃＝2。

根据与帧2相同的推理过程，响应时间计算如下：

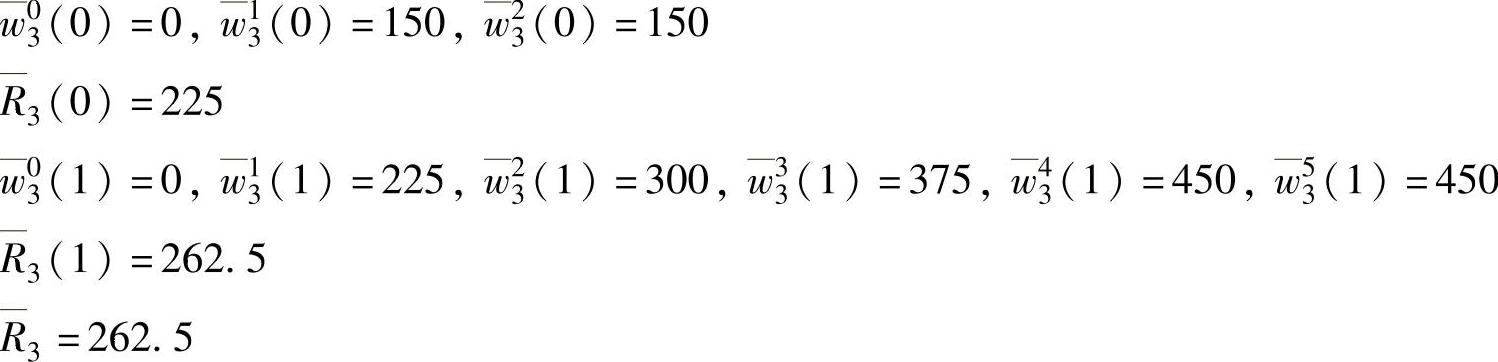
对以上过程总结如下：当我们使用精确分析而不使用充分分析，R₁≤D₁，R₂≤D₂，且R₃≤D₃时，整个帧集合为可调度。充分分析更加迅速，因为它要求完成的计算更少。在绝大多数情况下与精确分析相比，充分测试提供相同的可调度帧集合。然而存在像上述实例中的情况，只有通过精确分析才能显示出帧集合实际上是可调度的。