在线路中，除了水平的路段外，还不可避免的有上坡和下坡。两相邻坡段的交点称为变坡点。为了保证行车安全，在相邻坡段间要加设竖曲线。竖曲线按顶点所在位置又可分为凸形竖曲线和凹形竖曲线。图13-23中i1、i2、i3分别为设计的路面坡道线的坡度。上坡为正，下坡为负，θ为竖曲线的转折角。由于路线设计时的允许坡度一般总是很小的，所以可以认为θ等于相邻坡道之坡度的代数差，如θ1＝i2-i1，θ2＝i3-i2。θ大于零时为凹形竖曲线，θ小于零时为凸形竖曲线。为了书写方便，计算中直接用θ＝|θ|来计算。

图13-23　竖曲线

图13-24　竖曲线的计算

竖曲线可用抛物线或圆曲线表示。用抛物线过渡，在理论上似乎更为合理，但实际上用圆曲线计算与用抛物线计算结果是非常接近的，因此在公路中竖曲线都采用圆曲线。根据纵断面设计中给定的竖曲线半径R，以及由相邻坡道之坡度求得的线路竖向转折角θ，可以计算竖曲线长L、切线长T和外矢距E等曲线要素。由图13-24可以看出：

L＝R·θ＝R(i2-i1)　(13-33)

因为θ值一般都很小，而且竖曲线半径R都比较大，所以切线长T可近似以曲线长L的一半来代替，外矢距E0也可按近似公式来计算，则有：

切线长T求出后，即可由变坡点J沿中线向两边量取T值，定出竖曲线的起点Z和终点Y。

竖曲线上一般要求每隔10m测设一个加桩以便于施工。测设前按规定间距确定各加桩至竖曲线起（终）点的距离并求出各加桩点的设计标高（简称标高），以便在竖曲线范围内的各加桩点上标出竖曲线的高程。

在图13-24中，C为竖曲线上某个加桩点，将过C点的竖曲线半径延长，交切线于C′。令C′到起点Z的切线长为xC，CC′＝yC。由于设计坡度较小，可以把切线长xC看成是Z、C′两点间的水平距离，而把yC看成是C、C′两点间的高程差。也就是说，若按上述情况定义竖曲线上各点的x、y值，则竖曲线上任一点的x值即可根据其到竖曲线起（终）点的距离来确定，而它的y值即表示其在切线和竖曲线上的高程差。因而，竖曲线上任一点的标高（Hi）可按下式求得：

式中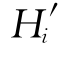：——该点在切线上的高程，也就是它在坡道线上的高程，称为坡道点高程；

Yi——该点的标高改正，当竖曲线为凸形曲线时取“-”，当为凹形曲线时取“＋”。

坡道点高程可根据变坡点J的设计高程H0、坡度i及该点至坡点的间距来推求，计算公式为：(www.daowen.com)

至于曲线上任一点的y值可根据该点的x值求得。由图13-24可知：

(R＋y)2＝R2＋x2

2Ry＝x2-y2

由于y与R相比很小，故可将y2略去，有：

从图中还可以看出，ymax≈E0，所以有：

【例13-3】　已知变坡点的里程桩号为K13＋650，变坡点设计高程H0＝290.95m，设计坡度为i1＝-2.5%，i2＝＋1.1%。现欲设置R＝2500m的竖曲线，要求曲线间隔为10m，求竖曲线元素和各曲线点的桩号及标高。

【解】　①由式（13-33）和式（13-34）计算竖曲线元素：

②计算竖曲线起、终点的里程：

表13-5　竖曲线算例