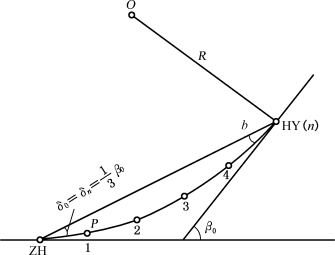
图13-10　缓和曲线偏角的计算

1）缓和曲线上偏角的特性

如图13-10，P点为缓和曲线上一点，根据式（13-12）缓和曲线方程：

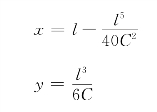
可求得其坐标xP、yP，则P点的偏角为：

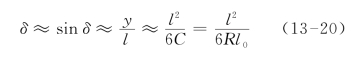
这是在缓和曲线起点测设缓和曲线上任意点偏角的基本公式，称为正偏角。反之，在缓和曲线上的P点测设缓和曲线起点的偏角为b，称为反偏角。由于P点的切线的倾角为β：

考虑式（13-11）：

β＝3δ　(13-21)

所以：

b＝β-δ＝3δ-δ＝2δ

故：

δ∶b∶β＝1∶2∶3　(13-22)

这一关系只有包括缓和曲线起点在内才正确，即δ必须是起点的偏角。

与圆曲线不同，缓和曲线上同一弧段的正偏角和反偏角不相同；等长的弧段偏角的增量也不等；如在起点的偏角是按弧长的平方增加的。(www.daowen.com)

2）缓和曲线上的偏角计算和测设

在实际应用中，缓和曲线全长都选用10m的倍数。为了计算和编制表格方便起见，缓和曲线上测设的点都是间隔10m的等分点，即整桩距法。当缓和曲线分为n段时，各等分点的偏角可用下述方法计算：

设δ1为缓和曲线上第1个等分点的偏角，δi为第i个等分点的偏角，则按式（13-20）可得：

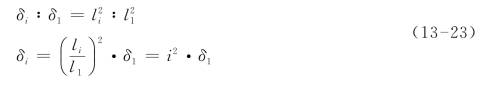
故第二点的偏角：

δ2＝22·δ1

第三点的偏角：

δ3＝32·δ1

……

第n点即终点的偏角：

而

因此，由β0→δ0→δ1这样的顺序计算出δ1，然后按22、32、…、n2的倍数乘以δ1求出各点的偏角，这比直接用公式（13-20）计算要方便。也可以根据缓和曲线长编制成偏角表，在实际作业中可查表测设。

如果测设的点不是缓和曲线的等分点，而是桩号为曲线点间距的整倍数时，此谓整桩号法，这时曲线的偏角严格按式（13-20）进行计算。

偏角法测设时的弦长，严密的计算法用相邻两点的坐标反算而得，但较为复杂。由于缓和曲线和圆曲线半径都较大，因此常以弧长来代替弦长进行测设。缓和曲线弦长的计算式为：

C0＝x0·secδ0