1）缓和曲线常数的计算方法

缓和曲线的常数有：缓和曲线的倾角β0、圆曲线的内移值P和切线的外延量m。

如图13-9，虚线部分为一转向角为α、半径为R的圆曲线AB，今欲在两侧插入长为l0的缓和曲线。圆曲线的半径R不变而将圆心从O′移至O点，使得移动后的曲线离切线的距离为p。曲线起点沿切线向外侧移至E点，设DE＝m，同时将移动后圆曲线的一部分（图中的C～F）取消，从E点到F点之间用弧长为l0的缓和曲线代替，故缓和曲线大约有一半在原圆曲线范围内，而另一半在原直线范围内。缓和曲线的倾角β0即为C～F所对的圆心角。这里缓和曲线的倾角β0、圆曲线的内移值p和切线的外延量m称为缓和曲线常数，其计算公式如下。

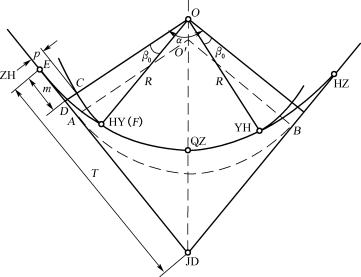
图13-9　缓和曲线连同圆曲线

由式（13-11）可知：

从图13-9中可以看出：

p＝y0-R·(1-cosβ0)

将式（13-13）及cosβ0展开式代入上式，可得：

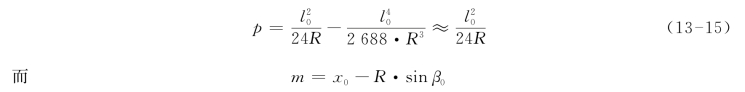
同样将式（13-13）及sinβ0的展开式代入上式，可得：

2）带有缓和曲线的圆曲线综合要素的计算

（1）圆曲线的曲线控制点

交点是曲线最重要的曲线控制点，用JD来表示，圆曲线的其他5个控制点是：直缓点ZH、缓圆点HY、曲中点QZ、圆缓点YH和缓直点HZ。

（2）圆曲线的要素和里程计算(www.daowen.com)

为了要测设这些控制点并求出这些点的里程，必须计算圆曲线要素，主要有切线长T、外矢距E、曲线长L和切曲差D。

如图13-9，各曲线要素计算公式如下：

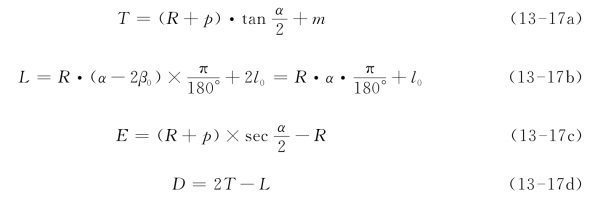
式中：R——圆曲线的半径；

α——转向角，其大小均由设计确定。

圆曲线上各点的里程都是从一已知里程的点开始沿曲线逐点推算。一般已知JD点的里程（JD里程是从前一直线段推算而得），再由它推算其他各控制点的里程。

ZH（里程）＝JD（里程）-T　（13-18a）

【例13-2】　已知一带有缓和曲线的圆曲线，转向角α＝24°36′48″，设计半径R＝500m，缓和曲线长l0＝80m，交点JD里程为K12＋382.40，计算缓和曲线常数、曲线的要素及曲线控制点里程。

【解】　①缓和曲线常数计算：

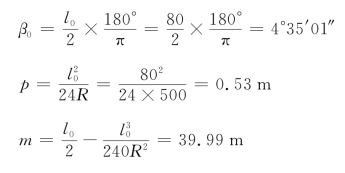
②圆曲线的要素计算：

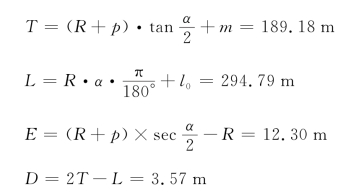
③曲线控制点里程计算及检核：